1. Smooth L1 Loss

对比 L1、L2 和 Smooth L1,

  • 定义分别为：

检测回归损失系列 - 图1%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%0A0.5%20x%5E%7B2%7D%20%26%20%5Ctext%20%7B%20if%20%7D%7Cx%7C%3C1%20%5C%5C%5C%5C%0A%7Cx%7C-0.5%20%26%20%5Ctext%20%7B%20otherswise%20%7D%0A%5Cend%7Barray%7D%5Cright.%0A%5Cend%7Barray%7D%0A#card=math&code=%5Cbegin%7Barray%7D%7Bl%7D%0AL%7B1%7D%3D%7Cx%7C%20%5C%5C%5C%5C%0AL%7B2%7D%3D%200.5%20x%5E%7B2%7D%20%5C%5C%5C%5C%0A%5Ctext%20%7B%20Smooth%20%7D%7BL%7B1%7D%7D%28x%29%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%0A0.5%20x%5E%7B2%7D%20%26%20%5Ctext%20%7B%20if%20%7D%7Cx%7C%3C1%20%5C%5C%5C%5C%0A%7Cx%7C-0.5%20%26%20%5Ctext%20%7B%20otherswise%20%7D%0A%5Cend%7Barray%7D%5Cright.%0A%5Cend%7Barray%7D%0A&id=FMOzw)

  • 梯度分别为：

检测回归损失系列 - 图2%7D%7Bx%7D%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bc%7D%0A1%20%5Cquad%20x%20%3E%200%20%5C%5C%5C%5C%0A-1%20%5Cquad%20x%20%3C%200%20%5C%5C%5C%5C%0A%5Cend%7Barray%7D%5Cright.%20%5C%5C%5C%5C%0A%5Cfrac%7Bd%20L%7B2%7D(x)%7D%7Bx%7D%3D%20x%20%5C%5C%5C%5C%0A%5Cfrac%7B%5Ctext%20%7B%20dSmooth%20%7D%20L%201%7B1%7D(x)%7D%7Bx%7D%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bcr%7D%0Ax%20%26%20%5Ctext%20%7B%20if%20%7D%7Cx%7C%3C1%20%5C%5C%5C%5C%0A%5Cpm%201%20%26%20%5Ctext%20%7B%20otherswise%20%7D%2C%0A%5Cend%7Barray%7D%5Cright.%0A%5Cend%7Barray%7D%0A#card=math&code=%5Cbegin%7Barray%7D%7Bl%7D%0A%5Cfrac%7Bd%20L%7B1%7D%28x%29%7D%7Bx%7D%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bc%7D%0A1%20%5Cquad%20x%20%3E%200%20%5C%5C%5C%5C%0A-1%20%5Cquad%20x%20%3C%200%20%5C%5C%5C%5C%0A%5Cend%7Barray%7D%5Cright.%20%5C%5C%5C%5C%0A%5Cfrac%7Bd%20L%7B2%7D%28x%29%7D%7Bx%7D%3D%20x%20%5C%5C%5C%5C%0A%5Cfrac%7B%5Ctext%20%7B%20dSmooth%20%7D%20L%201_%7B1%7D%28x%29%7D%7Bx%7D%3D%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bcr%7D%0Ax%20%26%20%5Ctext%20%7B%20if%20%7D%7Cx%7C%3C1%20%5C%5C%5C%5C%0A%5Cpm%201%20%26%20%5Ctext%20%7B%20otherswise%20%7D%2C%0A%5Cend%7Barray%7D%5Cright.%0A%5Cend%7Barray%7D%0A&id=VUYt5)

  • 三者对比：
    • L1 梯度稳定，对离群点不敏感，存在多个解，在训练后期梯度波动大，而 L2 对离群点敏感，总是有一个稳定解，训练初期可能会有梯度爆炸。
    • Smooth L1 是保留了 L1 和 L2 的优点，训练早期梯度稳定，训练后期总是有稳定解，能够收敛到更高的精度。
  • 存在的问题：
    • 优化边界框回归 和 提升IoU 不完全等价。

2. IoU Loss

边界框回归的一个假设是，坐标点是相互独立，而实际上坐标点具有一定的相关性。 从回归坐标到直接优化 IoU。

  • 每一个 gt 会 assign 给对应的 anchor，loss = - ious.log()。

iou-loss.jpeg

  • IoU loss 存在的问题：
    1. IoU = 0 无法优化
    2. IoU 无法确定具体检测框位置

iou-no-overlaps.jpeg

3. GIoU Loss

  • GIoU loss 是 IoU loss 的一个改进。

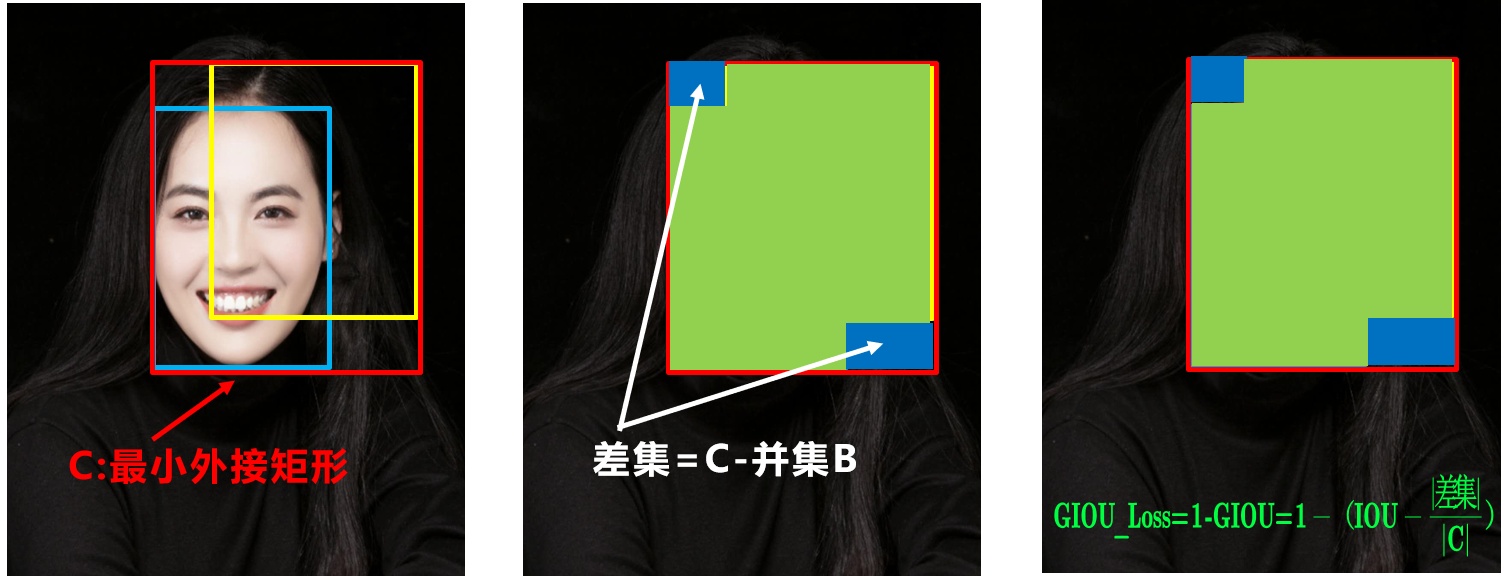
giou-loss.jpeg

  • GIoU loss 的不足：预测框和 gt 存在包含关系时，GIoU 退化成 IoU。

giou-contain.jpeg

4. DIoU Loss

  • 好的目标框回归函数应该考虑三个重要几何因素：重叠面积、中心点距离，长宽比。

diou-loss.jpeg

  • 存在的问题：中心点相同，存在包含关系，DIoU 退化成 GIoU。

giou-contain.jpeg

5.CIoU Loss

检测回归损失系列 - 图9%2Bv%7D%5Cright)%20%5C%5C%5C%5C%0A%5Cnu%3D%5Cfrac%7B4%7D%7B%5Cpi%5E%7B2%7D%7D%5Cleft(%5Carctan%20%5Cfrac%7B%5Cmathrm%7Bw%7D%5E%7Bg%20t%7D%7D%7B%5Cmathrm%7B~h%7D%5E%7Bg%20t%7D%7D-%5Carctan%20%5Cfrac%7B%5Cmathrm%7Bw%7D%5E%7Bp%7D%7D%7B%5Cmathrm%7Bh%7D%5E%7Bp%7D%7D%5Cright)%5E%7B2%7D%0A#card=math&code=%5Ctext%20%7B%20CIoU_Loss%20%7D%3D1-%5Cmathrm%7BCIoU%7D%3D1-%5Cleft%28%5Cmathrm%7BIoU%7D-%5Cfrac%7B%5Ctext%20%7B%20Distance%20%7D%202%5E%7B2%7D%7D%7B%5Ctext%20%7B%20Distance%20%7D%20%5Cmathrm%7BC%7D%5E%7B2%7D%7D-%5Cfrac%7B%5Cnu%5E%7B2%7D%7D%7B%281-%5Cmathrm%7BIoU%7D%29%2Bv%7D%5Cright%29%20%5C%5C%5C%5C%0A%5Cnu%3D%5Cfrac%7B4%7D%7B%5Cpi%5E%7B2%7D%7D%5Cleft%28%5Carctan%20%5Cfrac%7B%5Cmathrm%7Bw%7D%5E%7Bg%20t%7D%7D%7B%5Cmathrm%7B~h%7D%5E%7Bg%20t%7D%7D-%5Carctan%20%5Cfrac%7B%5Cmathrm%7Bw%7D%5E%7Bp%7D%7D%7B%5Cmathrm%7Bh%7D%5E%7Bp%7D%7D%5Cright%29%5E%7B2%7D%0A&id=LBxRK)

小结

Smooth L1: 综合了 L1 和 L2的优点。

IoU_Loss：主要考虑检测框和目标框重叠面积。

GIoU_Loss：在IoU的基础上，解决边界框不重合时的问题。

DIoU_Loss：在IoU和GIoU的基础上，考虑边界框中心点距离的信息。

CIoU_Loss：在DIoU的基础上，考虑边界框宽高比的尺度信息。