理解协方差矩阵

1. 方差和协方差的定义

在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来刻画两个随机变量的相似程度，其中，方差的计算公式为

其中， 表示样本量，符号 表示观测样本的均值。

在此基础上，协方差的计算公式被定义为

2. 从方差/协方差到协方差矩阵

对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，协方差矩阵为

其中 为对称矩阵。

3. 多元正态分布于线性变换

假设一个向量 服从均值向量为 、协方差矩阵为 的多元正态分布(multi-variate Gaussian distribution)，则

进一步简化为

再令 ，包含两个随机变量 和 ，则协方差矩阵可写成如下形式：

用单位矩阵(identity matrix) 作为协方差矩阵，随机变量 和 的方差均为1，则生成若干个随机数如图1所示。

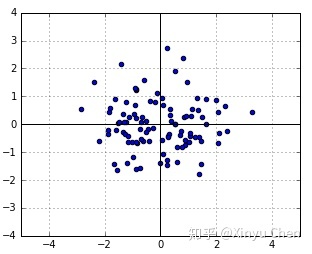
图1 标准的二元正态分布
在生成的若干个随机数中，每个点的似然为

对图1中的所有点考虑一个线性变换(linear transformation)： ，我们能够得到图2。

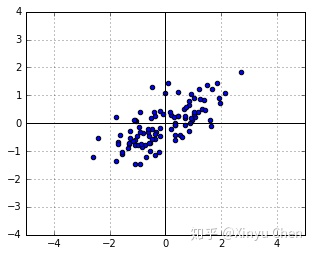
图2 经过线性变换的二元正态分布，先将图1的纵坐标压缩0.5倍，再将所有点逆时针旋转30°得到

在线性变换中，矩阵 被称为变换矩阵(transformation matrix)，为了将图1中的点经过线性变换得到我们想要的图2，其实我们需要构造两个矩阵：

1. 尺度矩阵(scaling matrix)：

1. 旋转矩阵(rotation matrix)

其中， 为顺时针旋转的度数。
变换矩阵、尺度矩阵和旋转矩阵三者的关系式：

另外，需要考虑的是，经过了线性变换， 的分布是什么样子呢？
将 带入前面给出的似然 ，有

由此可以得到，多元正态分布的协方差矩阵为

4. 协方差矩阵的特征值分解

对于任意对称矩阵 ，存在一个特征值分解(eigenvalue decomposition, EVD)：

其中， 的每一列都是相互正交的特征向量，且是单位向量，满足 ， 对角线上的元素是从大到小排列的特征值，非对角线上的元素均为 0。

其中，，因此，通俗地说，任意一个协方差矩阵都可以视为线性变换的结果。
在上面的例子中，特征向量构成的矩阵为

特征值构成的矩阵为

到这里，我们发现：多元正态分布的概率密度是由协方差矩阵的特征向量控制旋转(rotation)，特征值控制尺度(scale)，除了协方差矩阵，均值向量会控制概率密度的位置，在图1和图2中，均值向量为了零向量 ，因此，概率密度的中心位于坐标原点。