可以用动态规划的问题都能用递归。

  • 自顶向下的方法对应递归，借助函数调用自己，是程序解决问题的方式，它不会记忆解
  • 自底向上的方法对应动态规划，利用迭代将子问题的解存在数组（哈希表）里，从数组0位开始顺序往后计算
  • 递归的缺点在于包含重复的子问题（没有加记忆化的情况下），动态规划的效率更高

    思考方法

    1、找到一种可视化问题的方式

    通常使用有向无环图（DAG）。优点是将一个递增的子序列抽象为图中的一条路径。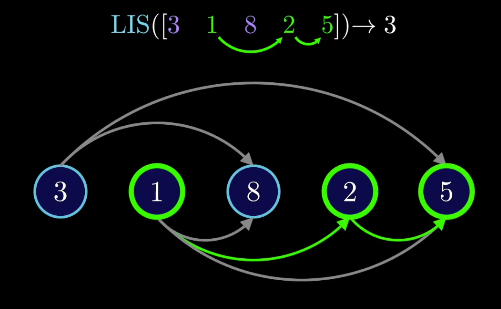
    动态规划 - 图1
    以LIS（最长递增子序列）问题为例，LIS的长度 = DAG中最长路径的长度+1（所加的1为结点）。

    2、找到一个合适的子问题

    通过起点或终点来刻画子集。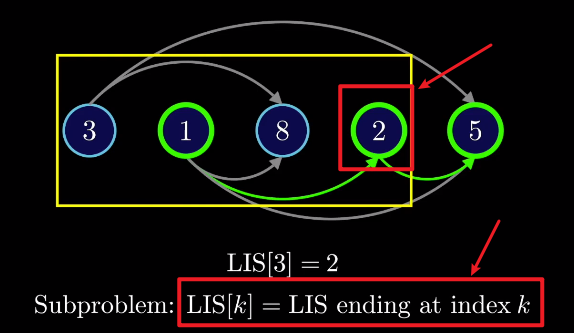
    动态规划 - 图2
    LIS[3]表示以序号3的结点作为终点的LIS的长度是多少。（LIS是1->2，所以LIS[3]=2）

    3、发现子问题间的内在联系

    例如，我想找到LIS[4]的答案，该怎样组合子问题呢？
    只需要找到指向序号为4的结点中LIS的最大值，然后加1就可以了。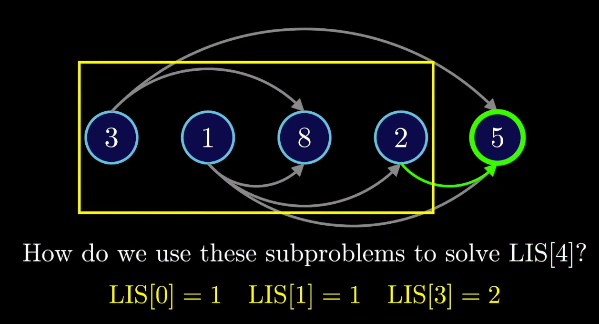
    动态规划 - 图3
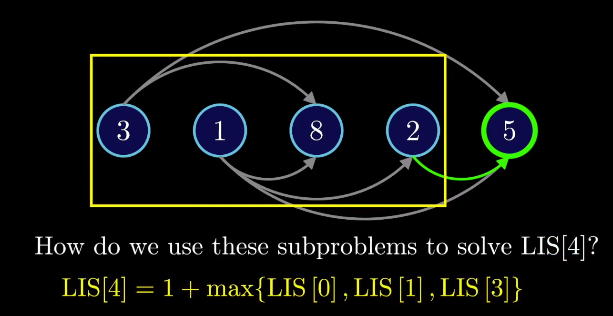
    动态规划 - 图4

    4、推而广之

    推广到任意的n。
    动态规划 - 图5

    5、以合适的方式解决子问题。

    确定并按正确方式解决子问题。
    例如从做向右。
    动态规划 - 图6

    6、汇总与变通

    如何从子序列的长度转变为子序列本身？使用前向索引。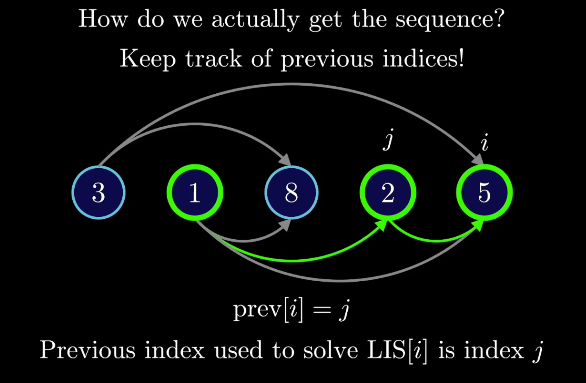
    动态规划 - 图7
    动态规划 - 图8

    例题：爬楼梯

    假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
    每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
    设 f(n) 表示爬 n 阶楼梯需要的跳法。那么，f(n) = f(n-1) + f(n-2)。