1.存储原理
sorted set,有序的 set,每个元素有个 score。score 相同时,按照 key 的 ASCII 码排序。
| 数据结构 | 是否允许重复元素 | 是否有序 | 有序实现方式 |
|---|---|---|---|
| 列表list | 是 | 是 | 索引下标 |
| 集合set | 否 | 否 | 无 |
| 有序集合zset | 否 | 是 | 分值score |
同时满足以下条件时使用 ziplist 编码:
元素数量小于128个
所有成员的长度都小于64字节
在 ziplist 的内部,按照 score 排序递增来存储。插入的时候要移动之后的数据。(时间换空间的思想)
# 与哈希和列表类似,排序后的集合也经过特殊编码,以节省大量空间。此编码仅在排序集的长度和元素低于以下限制时使用:zset-max-ziplist-entries 128zset-max-ziplist-value 64
超过阈值之后,使用 skiplist+dict 存储。
当 ziplist 作为 zset 的底层存储结构时,每个集合元素使用两个紧挨在一起的压缩列表节点来保存,第一个节点保存元素值,第二个元素保存元素的分值,而且分值小的靠近表头,大的靠近表尾。
zskiplist底层实现是跳跃表+字典。每个跳跃表节点都保存一个集合元素,并按分值从小到大排列,每个节点的 ele 属性保存了元素的值,score属性保存分值;字典的每个键值对保存一个集合元素,元素值包装为字典的键,元素分值保存为字典的值。注意集合的元素成员和分值是共享的,跳跃表和字典通过指针指向同一地址,不会浪费内存。
2.数据结构
2.1 跳表结构定义
zset的数据结构定义在server.h文件中。
typedef struct zset {//字典,键为成员,值为分值,可用于支持 O(1) 复杂度的按元素取分值操作dict *dict;//zsl: 跳跃表,按分值排序元素,用于支持平均复杂度为 O(log N) 的按分值定位元素的操作以及范围操作zskiplist *zsl;} zset;
字典前面我们已经说过了,再来看下zskiplist结构。
typedef struct zskiplist {struct zskiplistNode *header, *tail; /* 指向跳跃表的头结点和尾节点 *//* 链表包含的节点总数。新创建的 skiplist 包含一个空的头指针,这个头指针不包含在 length 计数中 */unsigned long length;int level; /* 最大的层数 */} zskiplist;
接着我们再来看一下组成了zskiplist的节点定义。
typedef struct zskiplistNode {sds ele; /* zset 的元素 */double score; /* 分值 */struct zskiplistNode *backward; /* 后退指针 */struct zskiplistLevel {struct zskiplistNode *forward; /* 前进指针,对应 level 的下一个节点 */unsigned long span; /* 从当前节点到下一个节点的跨度(跨越的节点数) */} level[]; /* 层 */} zskiplistNode;
2.2跳表的构建
t_zset.c文件中的zslInsert() 是跳跃表中非常关键的函数,这里体现了跳跃表的构建过程及其查找策略。可以看到 skiplist 为每个节点随机出一个层数(level),比如一个节点随机出的层数是3,那么就把它链入到从第1层到第3层这三层链表中。
- 首先通过分数 score 在跳跃表中查找到新增的节点应该插入的位置上的节点
- 调用 zslRandomLevel() 函数随机生成节点层数,使用该层数新建一个跳跃表节点
- 更新新增的节点应插入位置上的节点前后指针,将新增节点插入到跳跃表中
/* 在skiplist中插入一个新节点。假设元素不存在(由调用者强制执行)。skiplist获取传递的SDS字符串“ele”的所有权。 */zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;unsigned int rank[ZSKIPLIST_MAXLEVEL];int i, level;serverAssert(!isnan(score));//通过分数 score 在跳跃表中查找到新增的节点应该插入的位置上的节点x = zsl->header;for (i = zsl->level-1; i >= 0; i--) {/* store rank that is crossed to reach the insert position */rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];while (x->level[i].forward &&(x->level[i].forward->score < score ||(x->level[i].forward->score == score &&sdscmp(x->level[i].forward->ele,ele) < 0))){rank[i] += x->level[i].span;x = x->level[i].forward;}update[i] = x;}//随机生成节点层数level = zslRandomLevel();if (level > zsl->level) {for (i = zsl->level; i < level; i++) {rank[i] = 0;update[i] = zsl->header;update[i]->level[i].span = zsl->length;}zsl->level = level;}//使用生成的层数新建一个跳跃表节点x = zslCreateNode(level,score,ele);//更新新增的节点应插入位置上的节点前后指针,将新增节点插入到跳跃表中for (i = 0; i < level; i++) {x->level[i].forward = update[i]->level[i].forward;update[i]->level[i].forward = x;/* update span covered by update[i] as x is inserted here */x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);update[i]->level[i].span = (rank[0] - rank[i]) + 1;}/* increment span for untouched levels */for (i = level; i < zsl->level; i++) {update[i]->level[i].span++;}x->backward = (update[0] == zsl->header) ? NULL : update[0];if (x->level[0].forward)x->level[0].forward->backward = x;elsezsl->tail = x;zsl->length++;return x;}
2.3跳表的查找
有序链表
在这样一个链表中,如果我们要查找某个数据,那么需要从头开始逐个进行比较,直到找到包含数据的那个节点,或者找到第一个比给定数据大的节点为止(没找到)。也就是说,时间复杂度为 O(n)。同样,当我们要插入新数据的时候,也要经历同样的查找过程,从而确定插入位置。而二分查找法只适用于有序数组,不适用于链表。假如我们每相邻两个节点增加一个指针(或者理解为有三个元素进入了第二层),让指针指向下下个节点。
这样所有新增加的指针连成了一个新的链表,但它包含的节点个数只有原来的一半(上图中是 7, 19, 26)。在插入一个数据的时候,决定要放到那一层,取决于一个算法(在 redis 中 t_zset.c 有一个 zslRandomLevel 这个方法)。现在当我们想查找数据的时候,可以先沿着这个新链表进行查找。当碰到比待查数据大的节点时,再回到原来的链表中的下一层进行查找。比如,我们想查找 23,查找的路径是沿着下图中标红的指针所指向的方向进行的:

- 23 首先和 7 比较,再和 19 比较,比它们都大,继续向后比较。
- 但 23 和 26 比较的时候,比 26 要小,因此回到下面的链表(原链表),与 22比较。
- 23 比 22 要大,沿下面的指针继续向后和 26 比较。23 比 26 小,说明待查数据 23 在原链表中不存在。在这个查找过程中,由于新增加的指针,我们不再需要与链表中每个节点逐个进行比较了。需要比较的节点数大概只有原来的一半。这就是跳跃表。
为什么不用 AVL 树或者红黑树?因为 skiplist 更加简洁。
3.存储过程
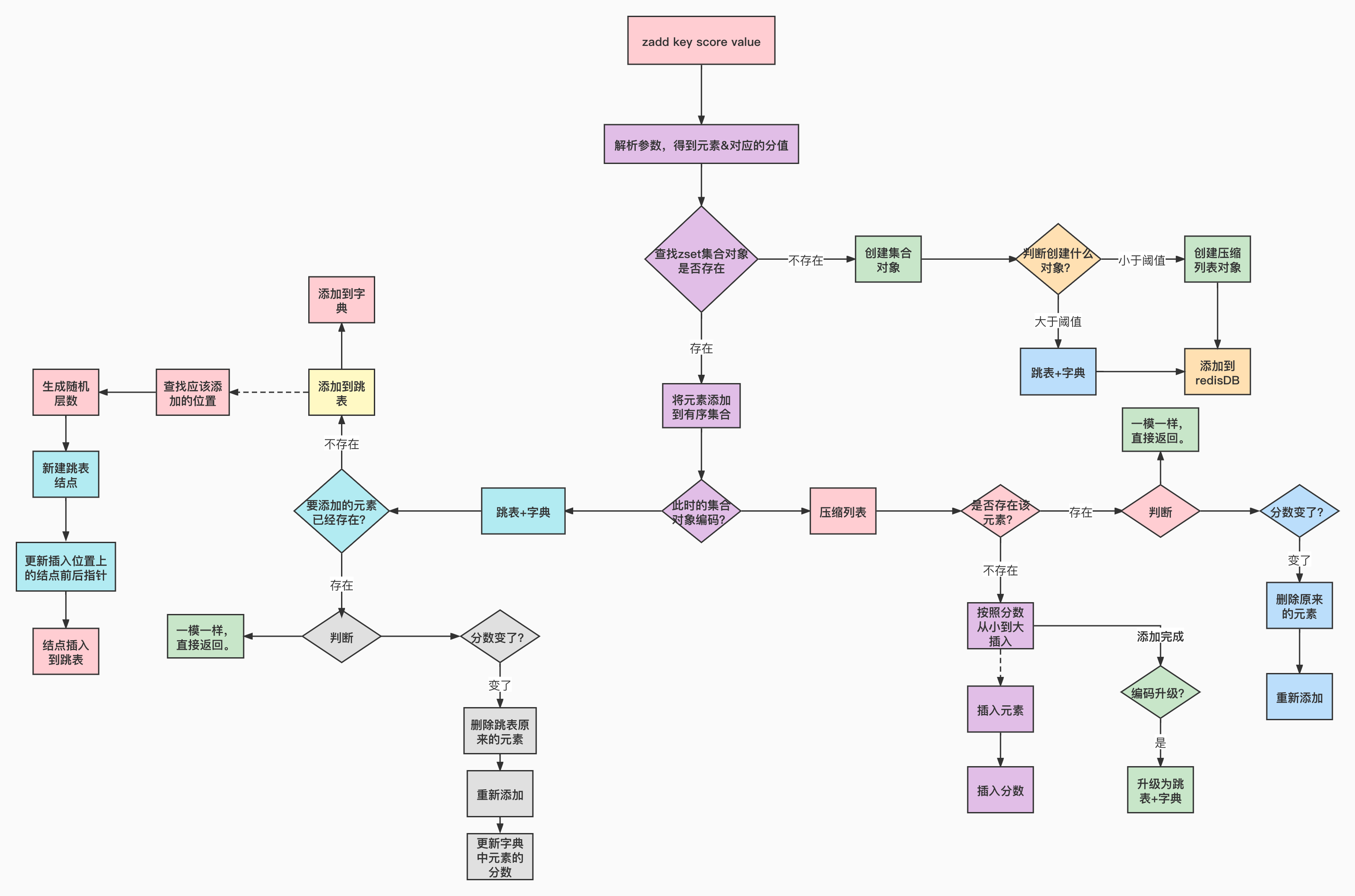
zset的操作命令的处理函数在t_zset.c 文件中,向zset添加元素调用的函数为t_zset.c文件的zaddCommand()。这个函数其实主要调用了t_zset.c文件的zaddGenericCommand()。
void zaddCommand(client *c) {
zaddGenericCommand(c,ZADD_NONE);
}
这个方法很长,但是核心逻辑其实并不复杂,很多都不是我们需要关心的内容,我们来大概梳理一下:
- 解析参数得到每个元素及其对应的分值
- 查找key对应的 ZSet 集合对象是否存在,不存在则创建
- 根据zset_max_ziplist_entries & zset_max_ziplist_value 这两个参数决定是创建压缩列表还是跳表
- 加入到redis数据库
循环调用 zsetAdd()函数将元素添加到有序集合中 ```java void zaddGenericCommand(client *c, int flags) { …
/ 参数校验 / ….
/ After the options, we expect to have an even number of args, since we expect any number of score-element pairs. / elements = c->argc-scoreidx; if (elements % 2 || !elements) {
addReplyErrorObject(c,shared.syntaxerr); return;} elements /= 2; / Now this holds the number of score-element pairs. /
//省略一些校验信息 … / 解析参数得到每个元素及其对应的分值 / scores = zmalloc(sizeof(double)*elements); for (j = 0; j < elements; j++) {
if (getDoubleFromObjectOrReply(c,c->argv[scoreidx+j*2],&scores[j],NULL) != C_OK) goto cleanup;}
/查找key对应的 ZSet 集合对象是否存在,不存在则创建 / zobj = lookupKeyWrite(c->db,key); if (checkType(c,zobj,OBJ_ZSET)) goto cleanup; if (zobj == NULL) {
if (xx) goto reply_to_client; /* No key + XX option: nothing to do. */ /*根据zset_max_ziplist_entries & zset_max_ziplist_value 这两个参数决定是创建压缩列表还是跳表。 */ if (server.zset_max_ziplist_entries == 0 || server.zset_max_ziplist_value < sdslen(c->argv[scoreidx+1]->ptr)) { zobj = createZsetObject(); } else { zobj = createZsetZiplistObject(); } //加入到redis数据库。 dbAdd(c->db,key,zobj);} //循环调用 zsetAdd()函数将元素添加到有序集合中 for (j = 0; j < elements; j++) {
double newscore; score = scores[j]; int retflags = flags; ele = c->argv[scoreidx+1+j*2]->ptr; int retval = zsetAdd(zobj, score, ele, &retflags, &newscore); if (retval == 0) { addReplyError(c,nanerr); goto cleanup; } if (retflags & ZADD_ADDED) added++; if (retflags & ZADD_UPDATED) updated++; if (!(retflags & ZADD_NOP)) processed++; score = newscore;} server.dirty += (added+updated);
reply_to_client: …
cleanup: … }
<a name="LZxUz"></a>
### 3.1 zset对象的创建
我们在看以下两种zset对象的创建:
```c
robj *createZsetObject(void) {
//分配内存
zset *zs = zmalloc(sizeof(*zs));
robj *o;
/*创建一个字典对象*/
zs->dict = dictCreate(&zsetDictType,NULL);
/*创建一个skiplist对象*/
zs->zsl = zslCreate();
/*创建一个redisobject对象*/
o = createObject(OBJ_ZSET,zs);
/*设置redisobject对象的编码为跳表*/
o->encoding = OBJ_ENCODING_SKIPLIST;
return o;
}
robj *createZsetZiplistObject(void) {
/*创建一个空的ziplist对象*/
unsigned char *zl = ziplistNew();
/*创建一个redisobject对象*/
robj *o = createObject(OBJ_ZSET,zl);
/*设置redisobject对象的编码为压缩列表*/
o->encoding = OBJ_ENCODING_ZIPLIST;
return o;
}
3.2 添加元素到集合
方法有一点长,但是逻辑不难理解,我们来梳理一下:先判断是什么编码
- 此时是压缩列表编码
- 如果要添加的元素已经存在?
- 一模一样,直接返回
- 看看是不是要增加分数
- 如果元素 score 改变了,则先删除 ziplist 中的元素然后重新添加
- 此事说明集合中原本不存在要添加的元素
- 这里的添加是根据 score 分数有序插入的,分数小的在 ziplist 头部,分数大的在尾部,元素和分数分两次操作插入到 ziplist 中,并且紧挨在一起
- 添加完成后,判断元素的长度是否超出限制或 ziplist 存储的元素个数是否超过最大限制?
- 超出限制则将底层结构转为 skiplist
- 如果要添加的元素已经存在?
此时是跳表编码,在跳跃表中元素是按照分数有序存储的,这样范围查找的时间复杂度为 O(logN);使用字典则能达到单个元素查找O(1)的时间复杂度,非常高效
- 如果要添加的元素已经存在?
- 一模一样,直接返回
- 看看是不是要增加分数
- 已经存在且分数变了,在跳跃表中查找到目标节点,将其删除并重新插入一个节点,完成后返回新的跳跃表节点用于更新字典中元素的分数
此时说明不存在
- 将节点添加到跳表里面
新增一个节点到字典
int zsetAdd(robj *zobj, double score, sds ele, int *flags, double *newscore) { .... /* 此时是压缩列表编码 */ if (zobj->encoding == OBJ_ENCODING_ZIPLIST) { unsigned char *eptr; // [zzlFind] 判断要添加的元素是否已经存在 if ((eptr = zzlFind(zobj->ptr,ele,&curscore)) != NULL) { /* 完全一样直接返回 */ if (nx) { *flags |= ZADD_NOP; return 1; } /* 看看是不是要增加分数 */ if (incr) { score += curscore; if (isnan(score)) { *flags |= ZADD_NAN; return 0; } if (newscore) *newscore = score; } /* 如果元素 score 改变了,则先删除 ziplist 中的元素然后重新添加 */ if (score != curscore && /* LT? Only update if score is less than current. */ (!lt || score < curscore) && /* GT? Only update if score is greater than current. */ (!gt || score > curscore)) { //删除 zobj->ptr = zzlDelete(zobj->ptr,eptr); //重新添加 zobj->ptr = zzlInsert(zobj->ptr,ele,score); *flags |= ZADD_UPDATED; } return 1; } else if (!xx) { //此事说明集合中原本不存在要添加的元素 //这里的添加是根据 score 分数有序插入的,分数小的在 ziplist 头部,分数大的在尾部, // 元素和分数分两次操作插入到 ziplist 中,并且紧挨在一起 zobj->ptr = zzlInsert(zobj->ptr,ele,score); //元素的长度是否超出限制或 ziplist 存储的元素个数是否超过最大限制? if (zzlLength(zobj->ptr) > server.zset_max_ziplist_entries || sdslen(ele) > server.zset_max_ziplist_value) //超出限制则将底层结构转为 skiplist zsetConvert(zobj,OBJ_ENCODING_SKIPLIST); if (newscore) *newscore = score; *flags |= ZADD_ADDED; return 1; } else { *flags |= ZADD_NOP; return 1; } //此时是跳表编码, // 在跳跃表中元素是按照分数有序存储的,这样范围查找的时间复杂度为 O(logN); // 使用字典则能达到单个元素查找O(1)的时间复杂度,非常高效 } else if (zobj->encoding == OBJ_ENCODING_SKIPLIST) { zset *zs = zobj->ptr; zskiplistNode *znode; dictEntry *de; de = dictFind(zs->dict,ele); if (de != NULL) { /* 存在并一模一样,直接返回 */ if (nx) { *flags |= ZADD_NOP; return 1; } curscore = *(double*)dictGetVal(de); /* 分数是否需要自增 */ if (incr) { score += curscore; if (isnan(score)) { *flags |= ZADD_NAN; return 0; } if (newscore) *newscore = score; } /* 已经存在且分数变了,删掉重新插入 */ if (score != curscore && /* LT? Only update if score is less than current. */ (!lt || score < curscore) && /* GT? Only update if score is greater than current. */ (!gt || score > curscore)) {//在跳跃表中查找到目标节点,将其删除并重新插入一个节点,完成后返回新的跳跃表节点用于更新字典中元素的分数 znode = zslUpdateScore(zs->zsl,curscore,ele,score); /* Note that we did not removed the original element from * the hash table representing the sorted set, so we just * update the score. */ dictGetVal(de) = &znode->score; /* Update score ptr. */ *flags |= ZADD_UPDATED; } return 1; } else if (!xx) {//不存在 ele = sdsdup(ele); //将节点添加到跳表里面 znode = zslInsert(zs->zsl,score,ele); //新增一个节点到字典 serverAssert(dictAdd(zs->dict,ele,&znode->score) == DICT_OK); *flags |= ZADD_ADDED; if (newscore) *newscore = score; return 1; } else { *flags |= ZADD_NOP; return 1; } } else { serverPanic("Unknown sorted set encoding"); } return 0; /* Never reached. */ }4.应用场景
- 如果要添加的元素已经存在?
①排行榜
id 为 6001 的新闻点击数加 1:
zincrby hotNews:20190926 1 n6001
获取今天点击最多的 15 条:
zrevrange hotNews:20190926 0 15 withscores