Lecture 3. Loss Functions and Optimization
Loss Function
在 Linear Classifier 的训练过程中,我们可能会得到一系列的 W 值,而这些 W 的值会有不同的表现。这个时候我们希望能有一个函数来表示我们对这个 W 值的表现的满意程度。这个函数就是 Loss Function。假设现在有数据集 %5C%7D_%7Bi%3D1%7D%5E%7BN%7D#card=math&code=%5C%7B%28x_i%2C%20y_i%29%5C%7D_%7Bi%3D1%7D%5E%7BN%7D&id=ejT6l) ,其中  是图片,  是(整数)标签,那么对这个数据集和当前 W 的 loss function 是:
%2Cyi)%0A#card=math&code=L%3D%5Cfrac1N%20%5CSigma%7Bi%3D1%7D%5EN%20L_i%28f%28x_i%2CW%29%2Cy_i%29%0A&id=qyp8J)
Multiclass SVM loss
一种 loss function 叫做 Multiclass SVM loss ,有如下的  计算方式(#card=math&code=s%20%3D%20f%28x_i%2CW%29&id=jVcYP), 表示  的第  行):
%0A#card=math&code=Li%20%3D%5CSigma%7Bj%5Cneq%20yi%7D%20max%280%2C%20s_j%20-%20s%7By_i%7D%2B1%29%0A&id=buzwM)
即
这里的 1 是设定的安全边际。公式对应的图像为:
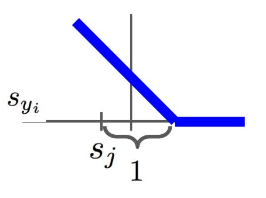
这种 loss function 被称为 Hinge Loss ,在安全边际之前 loss function 线性降低,而之后其值为 0 。
计算这类 loss function 的 python 代码如下:
def L_i_vectorized(x, y, W):
scores = W.dot(x)
margins = np.maximum(0, scores - scores[y] + 1)
margins[y] = 0
loss_i = np.sum(margins)
return loss_i
事实上仅仅通过这样的 loss function 很容易导致的一个问题就是训练得到的模型过于拟合训练数据,但实际上我们并不关心训练数据。我们希望它面对测试数据的时候也能有很好的表现。但是过于拟合训练数据的模型往往在面对新数据的时候表现并不好。如下图,蓝色点表示训练数据,蓝线表示拟合的模型(这不是线性的,是一个更一般的例子),绿色方块表示测试数据。可以看到尽管这条蓝线对蓝色点的拟合非常好,但是当面对绿色方块的时候,它的表现就不是那么优秀了。实际上我们更希望得到的是绿色的这条线。
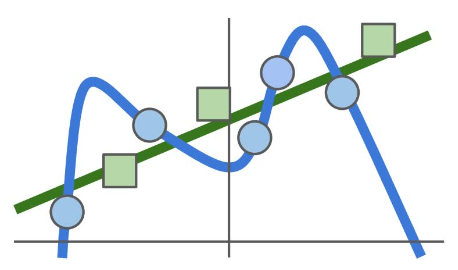
对于这个问题,通常我们选择在 loss function 后再加一项 regularization ,这一项鼓励模型在训练的过程中选择更简单的那一种,以期在测试数据上得到更好的表现(由奥卡姆剃刀原理的思想),如下:
%20%3D%20%5Cfrac1N%20%5CSigma%7Bi%3D1%7D%5EN%20L_i%20%2B%20%5Clambda%20R(W)#card=math&code=L%28W%29%20%3D%20%5Cfrac1N%20%5CSigma%7Bi%3D1%7D%5EN%20L_i%20%2B%20%5Clambda%20R%28W%29&id=K5hoE)
这里的  也是一个超参数,用于调整  和 #card=math&code=R%28W%29&id=KCU7D) 之间的比例。
一些常用的 #card=math&code=R%28W%29&id=lRswD)如下:
| formula | |
|---|---|
| L1 regularization | |
| L2 regularization | |
| Elastic net(L1 + L2) | |
| Dropout | … |
| … | … |
Softmax Loss
另一种计算方式是 Softmax ,这种计算方式如下:
%20%3D%20%5Cfrac%7Be%5E%7Bs_k%7D%7D%7B%5CSigma_j%20e%5E%7Bs_j%7D%7D%20%5C%20%5C%20%5C%20%5C%20%5C%20s%20%3D%20f(x_i%2CW)%0A#card=math&code=P%28Y%3Dk%20%7C%20X%20%3D%20x_i%29%20%3D%20%5Cfrac%7Be%5E%7Bs_k%7D%7D%7B%5CSigma_j%20e%5E%7Bs_j%7D%7D%20%5C%20%5C%20%5C%20%5C%20%5C%20s%20%3D%20f%28x_i%2CW%29%0A&id=TTGDV)
%0A#card=math&code=L_i%20%3D%20-logP%28Y%3Dy_i%7CX%3Dx_i%29%0A&id=alROI)
即:
%0A#card=math&code=L_i%20%3D%20-log%28%5Cfrac%7Be%5Es%7By_i%7D%7D%7B%5CSigma_j%20e%5E%7Bs_j%7D%7D%29%0A&id=DGtAf)
Softmax vs. SVM
两种 loss function 的计算过程示意图如下:
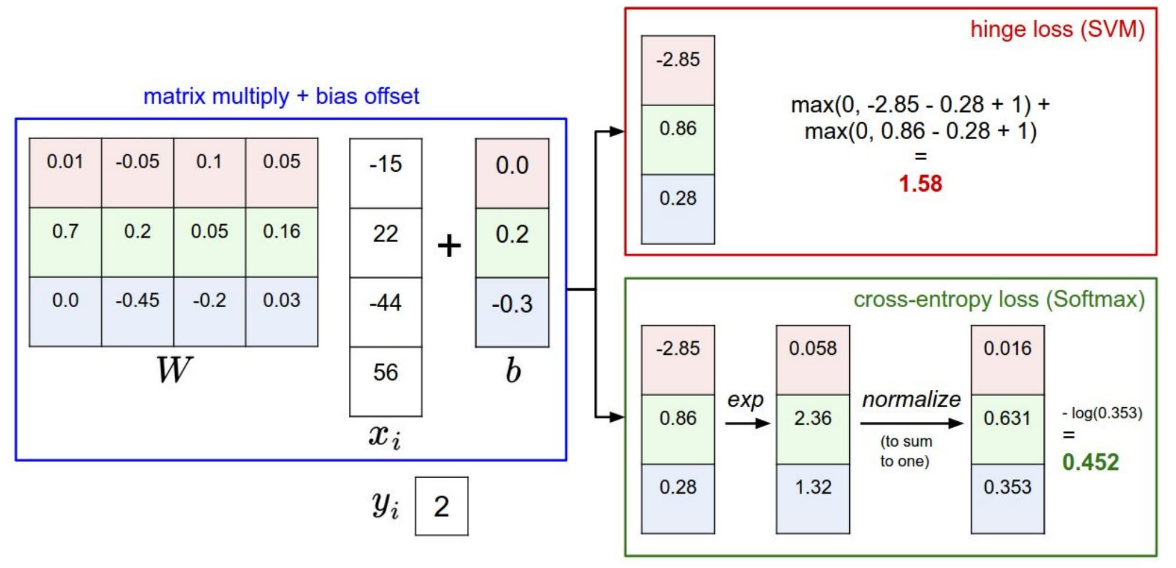
两者之间一个很大的区别在于,对于 SVM ,它关心的是正确分类的得分是否比其他得分高,只要正确得分确实比其他得分 + 安全边际要高,那么得到的  就是 0 ,也就是说它的目标就是正确分类得分大于错误得分 + 安全边际。而对于 Softmax 而言,它总是希望正确分类的概率能够达到 1 ,也就是正确的得分趋向正无穷,而其他得分趋向负无穷(当然计算机对无穷的支持并不是那么优秀)。因此,不管现在训练的模型如何, Softmax 总是希望这个模型能够训练得更好。P. S. 从实际应用上来看两者并没有那么大的区别。
Optimization
那么,有了 loss function 以后,我们已经知道如何评估一个 W 矩阵的表现。那么,我们如何才能找到表现最优的那个 W 矩阵呢?
首先最容易想到的办法就是随机搜索,每次随机一个 W 矩阵,然后看这个矩阵表现如何,如果比当前最优的模型优那么就更新。显然,这种方法非常愚蠢,效率低下且训练结果也很难保证。
另一种想法是对于当前的 W 矩阵,我们试图去寻找其附近的局部最优解,并希望不断重复这个过程能够引领我们找到全局最优解。当然这很可能是找不到的,但即便如此,不断地找寻局部最优解这样的方法在实践中依然表现出了非常优秀的结果。
对 1 维的直线而言,寻找局部最优非常简单,只需要在当前位置的极限即可计算,如下:
%7D%7Bdx%7D%20%3D%20%5Clim%5Climits%7Bh%20%5Crightarrow%200%7D%20%5Cfrac%7Bf(x%20%2B%20h)%20-%20f(x)%7D%7Bh%7D%0A#card=math&code=%5Cfrac%7Bdf%28x%29%7D%7Bdx%7D%20%3D%20%5Clim%5Climits%7Bh%20%5Crightarrow%200%7D%20%5Cfrac%7Bf%28x%20%2B%20h%29%20-%20f%28x%29%7D%7Bh%7D%0A&id=UogHB)
而对多维而言,则需要用到梯度的概念。梯度是一个向量,其每一个维度的值是函数在这个维度的斜率。由数学推导可知,函数在一点沿梯度方向变化最大,也就是说可以利用梯度来求得局部最优的 W 矩阵。
在计算梯度的时候,也有两种不同的做法。一种是通过每次给 W 的一个维度加上一个很小的量,然后计算出两次 f(W)的值的差别,再除上这个很小的量,得到梯度在这个维度的值。这个方法的效率很低且精度有限,并不好。更好的方法是利用微积分的知识来求得梯度。当然数值计算的方法并非完全没有用,恰恰相反,利用数值计算来检验微分计算的正确性是很常见的手法,因为微分分析很容易出错。
有了梯度以后,我们便可以得到一个非常简短却是很多深度学习的核心思路的代码:
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += -step_size * weights_grad
实际操作中还有一个小技巧。由于 loss function 的计算需要把所有数据的 loss 取平均,因此当数据量很大的时候每一次计算梯度都需要耗费非常多的时间。因此在计算梯度的时候,我们会考虑从所有的数据集中随机地取出一部分来代替所有数据,如下:
while True:
data_batch = sample_training_data(data, 256)
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += -step_size * weights_grad
Image Features
事实上,由于多模态等原因,直接将图片像素信息不加任何处理地送进线性分类器,得到的结果往往不慎理想。因此在深度神经网络之前,人们往往采用两步来进行模型的训练。首先是将图片中的一些特征信息提取出来,计算得到数值,然后再把这些数值送进线性分类器。当然这个提取信息的过程需要根据图片信息而定。一个很简单的例子是在二维平面上的一些点。如果用经典的笛卡尔坐标系,则很难用线性分类进行区分;但如果进行特征提取转换为极坐标,那么就比较容易可以用线性分类器分开。

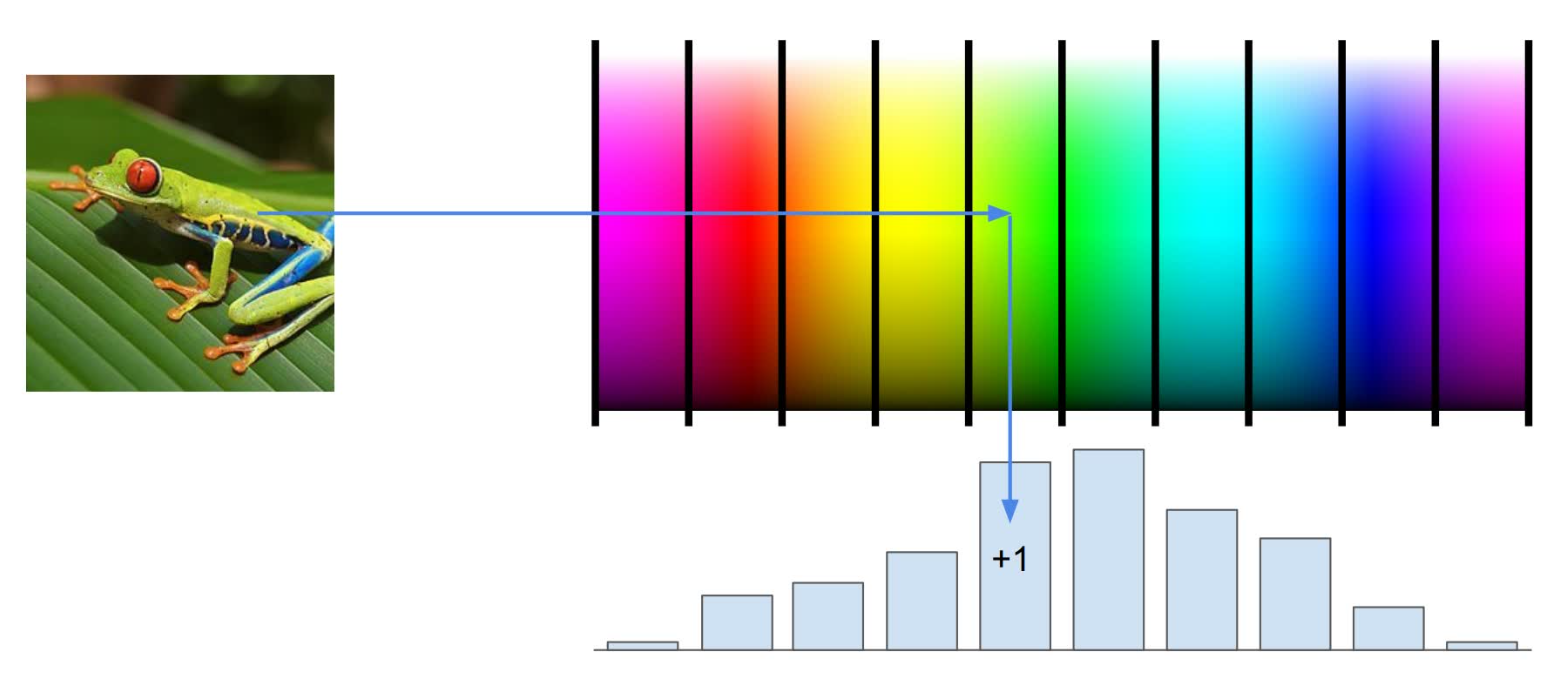
应用到实际中,一种常见的特征值提取叫做 Color Histogram (颜色直方图)。这种方法是将颜色大致分为几种,然后把每一个像素点的颜色按照分类计数。例如下图中的青蛙,得到的特征值中的绿色数量就占大多数。
还有一种很常见的特征值是 Histogram of Oriented Gradients 。上一讲有讲到边缘对视觉识别非常重要,因此提取边缘特征放进训练也是一种很好用的方法。例如把一张图分为 8 × 8 的小区域,每一个区域中有 9 个方向信息,这样一张 320 × 240 的图片就可以用 10800 个数来表示其边缘特征值。


