| 书籍《学习JS数据结构与算法 第三版》[x] 书籍 [ ] 讲座 [ ] 视频 | |||
|---|---|---|---|
| 作者 | [巴西]洛伊安妮·格罗纳 | 出版社 | 人民邮电出版社 |
| ISBN | 9787115510174 | 出版时间 | 2019-5 |
| 豆瓣网址 | 豆瓣 | 是否有电子版 | 图灵 微信读书 |
| 阅读日期 | 2020-12-3 | 更新日期 | |
| 相关链接 | Github仓库 | 备注 |

全书结构大致如下:
- 第一章 js简介 略过
- 第二章 es和ts概要 略过
3 数组
本章比较简单,但选择回顾,这是基础中的基础,尤其是数组的api操作,虽然没几个
var arr = [1,2,3];// 后端插入 pusharr.push(5)arr.push(5,6)// 后端删除 poparr.pop()// 开头插入 插入费劲 unshiftarr.unshift(0)// 开头删除arr.shift()// 任意位置添加或删除元素arr.splice(5,3) // 索引,删除个数,后续添加元素
4 栈 Stack
克隆本文最上方提供的GitHub仓库了。进入 examples ,执行 http-server 可以观看页面和控制台。
4.1 数据结构
像子弹仓,后加入的在栈顶,先加入的再栈底部。
有啥用?比如:浏览器的历史记录。
4.2 技术实现
接下来实现一个 Stack类
实现下面的方法:
push(elements)添加新元素到栈顶。- pop 移除栈顶元素,并返回
- peek 找到栈顶元素,只查找不变动
- isEmpty 是否有有元素
- clear 移除所有元素
- size 栈内的个数
不难想象,我们可以使用js的数组来进行操作,每次操作都是 push和 pop 的操作。
class Stack {constructor() {this.items = []}// 添加push(element) {this.items.push(element)}// 移除最后一个并返回pop() {return this.items.pop()}// 查看最后一个peek() {return this.items[this.items.length-1]}// 是否为空isEmpty() {return this.items.length === 0}// 元素个数size() {return this.items.length}}
看着不难,走出了第一步,循序渐进
4.3 使用栈
const stack = new Stack()stack.push(1)// xx
但这种实现方式,时间复杂度是 O(n) ,如何更快?我们使用js的对象来完成。
4.4 技术实现2
class Stack {constructor() {this.items = {}this.count = 0}push(element) {this.items[this.count] = element;this.count++ // 通过这种方式完成了数组的存放}size(){return this.count}isEmpty(){return this.count===0}pop() {if(this.isEmpty){return undefined}// 找到元素,删掉并返回this.count--const r = this.items[this.count]delete this.items[this.count]return r}peek() {if(this.isEmpty){return undefined}return this.items[this.count-1]}clear(){this.count=0this.items={}}}
通过维护对象和数字的方式,我们成功把时间复杂度讲到了 O(1) ,实现了指哪打哪。
要保护内部变量不被修改
方案一,下划线口头约定
方案二,我们对 item的key定义为 Symbol ,但这样依然可以通过 Object.getOwnProperty-Symbols 来进行修改
方案三, weakMap
const items = new WeakMap()class Stack {constructor() {items.set(this,[]) // 实例自身为key,值是数组}push(element) {const s = items.get(this) // 后续都是获取再使用s.push(element)}pop() {const s = items.get(this)const r = s.pop()return r}}
知晓即可,可读性不强,拓展时候无法继承。
方案四,未来有一个 # private 修饰符。但依然是编译时候有用。
4.5 解决问题
从十进制到二进制。
比如10,对应的二进制如何求?就可以使用这个stack,这里我手写一个试试
const stack=new Stack()const n=10while(n>0){cosnt y = n%2 // 0,1,0,1stack.push(y)const n = Math.floor(n/2) // 5,2,1,0}// 此时 stack=0101 这个时候翻转即可let str=''while(!stack.isEmpty()) {str+= stack.pop().toString() // 1 0 1 0return str}
稍作修改,就可以改为其他进制。因为不同进制的表示不同,所以我们直接定义一个数字表
const num = '0123456789ABCDEFGHIJIK'
需要把余数进行映射,比如八进制中余数7 映射为7,如果是二进制,11映射为B之类的。
此外还有汉诺塔 hanoiStack
这个汉诺塔,我们从一个大的问题,不断(这就意味着递归)拆分成小的问题。
5 队列和双端队列
5.1 队列数据结构
队列就先个排队,先入先出。
从简单的技术实现开始
class Queue {constructor() {this.count = 0;this.lowestCount = 0;this.items = {};}}
我们依然需要通过 count 和 items 来实现内容的存储,因为每次都会操作队首,我们需要一个lowestCount来存储第一个。
我们来补充一些功能:
- enqueue 添加到尾部
- dequeue 移除第一个并返回
- peek 获取第一个
- isEmpty
- size
技术实现
class Queue {// 添加enqueue(element) {this.items[this.count] = element;this.count++}// 移除dequeue(){if(this.isEmpty()) {return undefined;}const r = this.items[this.lowestCount];delete this.items[this.lowestCount]this.lowestCount++return r}// 查看第一个peek() {if(this.isEmpty()) {return undefined;}return this.items[this.lowestCount]}// 获取长度isEmpty() {return this.count - this.lowestCount === 0// or// this.size() === 0}size() {return this.count - this.lowestCount}// 清空clear() {this.imtes={}this.count=0;this.lowestCount = 0;}}
api的操作这里略过。
5.2 双端队列数据结构
应用场景:用户的每个操作都会记录到一个栈里,我们如果撤销会弹出一个操作。
但最大只能记录比如20条,超出的会把栈底也移除,这又是 队列的操作。
因此栈和队列的结合是双端队列。
技术实现
这块是糅合,感觉不复杂。
addFront(element) {// 判断为空,直接 addBack(element)// 如果当前 lowestCount > 0,数值-1直接赋值// 如果是0需要整体移动for(let i = this.count; i>0;i--){this.items[i] = this.items[i-1]}this.count++this.lowestCount=0this.imtes[0]=element}
操作稍多,但是很容易理解。
解决问题
1. 击鼓传花。
循环队列
比如一群人围在一起,花依次传递,每次停止会退出一个,直到结束。
请实现这个函数
const names = [1,2,3,4,5]const r = hotPotato(names,7)// r.elininated [] 淘汰人// r.winner 最后剩下的人
思路,每次迭代names,把第一个移动到最后,如果是7就停止。
2. 回文
比如 madam 上海自来水来自海上
方法很多,但反向排列字符串,然后做对比是最简单的。
如果和反向排列字符串?只能使用 双端队列的话,每次取首尾做对比即可。
3. 事件循环
提到事件循环自然会 想到这篇文章 https://jakearchibald.com/2015/tasks-microtasks-queues-and-schedules/
6 链表 LinkList
6.1 数据结构
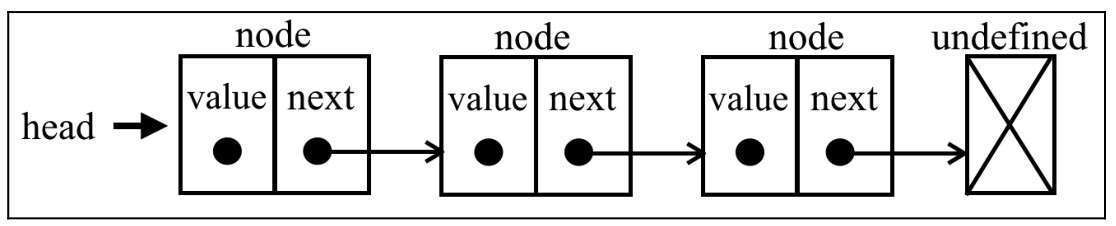
观察上图,链表的特点是,拥有一个 value 和 next 指针,指针指向下一个。
好处是移动或者增删元素,不需要移动其他元素,但是只能从头开始查找。
和数组显然是对立的。比如火车,一列一列连起来的。
6.2 技术实现
class LinkList {constructor(equalsFn = defalutEquals){this.count = 0; // 存储数量this.head = undefined; // 第一个元素引用this.equalsFn = equalsFn; // 对比是否相等 a===b}}// 结构class Node {constructor(element){this.element = element;this.next = undefined;}}
我们要准备下面的方法:
push(ele)尾部添加一个新元素insert(ele, position)特定位置插入元素getElementAt(index)获取特定位置的元素remove(ele)移除元素indexOf(ele)返回索引removeAt(position)移除特定位置的一个元素isEmpty()如果链表不包含任何元素,返回truesize()toString()值输出value
实现 push
class LinkList {// xx// 插入元素push(ele) {const node = new Node(ele)let current;if(this.head == null) { // 如果是空的this.head = node // 设置第一个} else {current = this.head // 如果不是空的,先填充current指针while(current.next != null) {current = current.next // 一直找到最后一个}current.next = node // 给最后一个的next指向当前元素}this.count++ // 数值++}}
思路比较明确。
实现 removeAt
class LinkList {removeAt(index) {// 判断index合法if(index >=0 && index < this.count) {let current = this.head;if(index === 0){ // 如果移除第一个,直接修改指针this.head = current.next} else {let prev;// index之前的都捋一遍for(let i=0;i<index;i++) {prev = current;current = current.next;}// 停止时候 能拿到 prev 和 nextprev.next = current.next}this.count--;return current.element}return undefined}}
总之就是找到关键节点,保留上一个节点,直接跳过current
实现 getElementAt
通过索引找到元素
class LinkList {getElementAt(index) {if(边界){let node = this.headfor(let i=0;i<index&&node!=null;i++) {node = node.next}return node}return undefined}}
我们封装这个方法,可以在上一个 removeAt 中使用。因此我们可以重构
class LinkList {removeAt(index) {// 判断index合法if(index >=0 && index < this.count) {let current = this.head;if(index === 0){ // 如果移除第一个,直接修改指针this.head = current.next} else {const prev = this.getElementAt(index-1);current = prev.next;prev.next = current.next}this.count--;return current.element}return undefined}}
少了一些代码,看起来更容易阅读。
实现 insert
insert(element,index){if(边界) {const node = new Node(element)if(index === 0){ // 在最前面添加,直接挂上去const current = this.head;node.next = current;this.head = node;} else {const prev = this.getElement(index - 1)const current = prev.next;node.next = currentprev.next = node}this.count++return true}return false}
思路也相对清晰。
实现 indexOf 也相对简单
有了indexOf ,删除某个元素也简单
isEmpty size getHead 都比较简单。
6.3 双向链表
下面是双向链表:
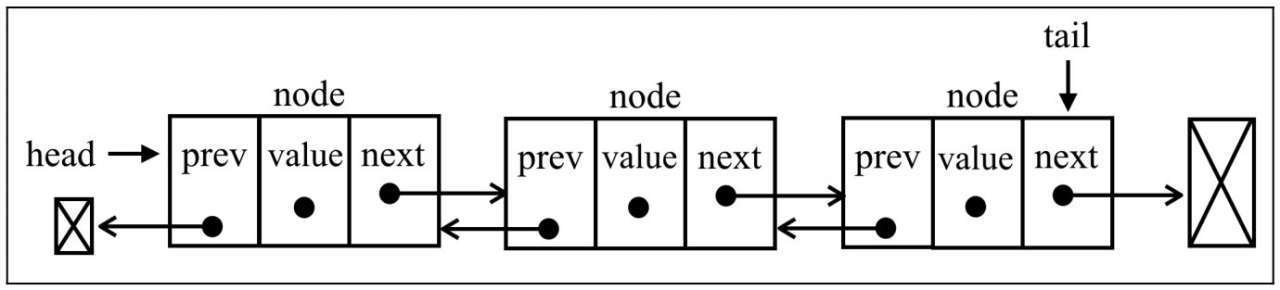
和单项链表相比,多了 prev 是一个完整体。
class DoublyNode extends Node {constructor(element, next, prev){super(element,next)this.prev = prev}}class DoublyLinkedList extends LinkedList {constructor(equalsFn){super(equalsFn)this.tail = undefined; // 最后一个引用}}
实现insert
insert(element, index) {if(边界){const node = new DoublyNode(element);let currrent = this.head}}
6.2.1
6.4 循环链表
在单向链表的基础上,最后一个指向第一个,形成循环单向链表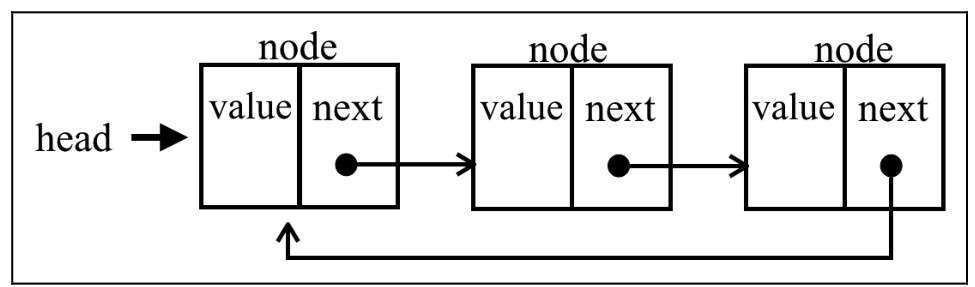
此外也有双向循环链表。
6.5 有序链表
SortedLinkedList 元素有序,可以使用排序算法,还可以插入元素
6.6 链表实现栈
实现 StackLinkedList
7 集合
7.1 数据结构
集合是不允许值重复的顺序数据结构,并且存在 交、差、并集
7.2 技术实现
这里我们使用对象来表示集合,也因为js对象的key是唯一的,保证集合的元素唯一。
class Set {constructor() {this.items = {}}}
依然要实现:
- add(ele) 添加元素
- delete(ele) 移除元素
- has(ele) 元素是否在集合中
- clear 移除集合的所有元素
- size 返回数量
- values 返回所有值的数组
我看了内容相对简单,后续的 js原生Set类也完美解决此类问题。
特点是
var set = {}
为啥原生Set有这些原生方法,是带着使命来的。
7.3 集合运算:交并差
8 字典和散列表
内容:
- 字典数据结构
- 散列表数据结构
- Map WeakMap WeakSet
在集合Set中,我们key和value相同。在字典Dict 中使用 key-value 存储结构
在 散列表中也是 key-value,实现略有不同。
8.1 字典
Dictionary
字典也叫 映射、符号表、关联数组。
我们可以使用 Map 来实现字典。
要实现下面的方法:
- set(key,value) 添加或者覆盖
- remove(key) 删除
- hasKey(key) 查看是否存在某个key
- get(key) 查找key
- clear() 删除所有值
- size() 字典个数
- isEmpty() 是否为空
- key() 获取所有的key,返回数组
- values() 获取所有的数值,返回数组
- keyValues() 返回所有的 key-value
- forEarch(fn) 迭代所有,回调返回false时候终止
8.2 散列表
HashTable 也叫 HashMap 类。这是 Dict的一种是散列表实现方式。
散列算法的作用是尽可能快找到一个值,在字典中如果要找一个值,得迭代器去查找。
如果使用 散列函数,就能知道值的具体位置,通过值找到地址。
在脚手架中的应用,对数据库进行索引。
在js内部就是使用散列表来表示每个对象。
lose lose 散列函数
要实现的话:
- put(key, value) 散列表增加一个项
- remove(key) 移除
- get(key) 搜索特定的值
这里跳的太快,如果数据冲突会丢失数据。要解决冲突有几种方法:
- 分离链接
- 线性探查
- 双散列发
djb2 散列函数。比较推崇
8.3 Map 类
9 递归
理解递归、基本应用、js调用栈
这部分抽离到 JS函数的递归部分
10 树
散列表之后的另一个非顺序数据结构,树。
概念、二叉搜索树、遍历、AVL树
10.2