背景
随着前端领域的快速发展,前端技术越来越多的被应用在更多领域。除了常规的Web、Hybrid,还有IoT等较为新潮的领域。在高速的发展下,前端的限制也逐步被体现出来:
- 有一些UI是高度重复的,例如一些落地页、营销页面。大部分公司的解决办法是搭建low code甚至no code平台,通过配置自动生成这些页面,或者通过聘请外包员工降低成本。lowcode和nocode方案的缺点是灵活程度不够。外包人员的流动性大、代码质量不稳定、容易造成项目难以维护。
- 前端需求多而杂。面对类似的功能,或许绑定不同的数据就是一个新的需求。常规的模块化代码在面对变动的数据和需求时,还是需要前端介入。
如果说现在最火的方案是serverless和自动化测试。那么今年开设的D2技术论坛,给前端行业未来五到十年确定了一个新的命题:前端智能化。
什么是前端智能化呢?简单地说就是利用AI技术,提升前端生产力,把部分可以重复的工作交给一套AI系统。这套系统的使用者是PD、PM等,前端的工作是根据PD的数据,重复训练这套AI,维护更高的可用性。目前业界可以达到的水平是PD稿经过标注后,直出项目,准确率已经可以达到80%左右。
AI智能化和模块代码不同。模块代码是生成固定的模块,节省了编写重复代码的时间;而AI智能化是可以根据业务的长期习惯,直接构建我们需要的项目。
除了在nocode方便的贡献,前端智能化也带来了很多新的用户交互场景。例如,在直播中,主播可以通过一些手势,触发直播间的节日特效,营造更好的直播氛围。而这些“黑科技”技术实现,就是来自于AI技术。
作为火了好几年的AI技术,目前已经有较为成熟的库和model可以直接使用,例如tensorflow.js。而我们大部分前端开发者,注重的是业务和UI操作逻辑,对数据和算法的理解不是很好,所以这里我们通过一个简单的样例的实现,让大家可以开始接触这个充满“魔法”的世界。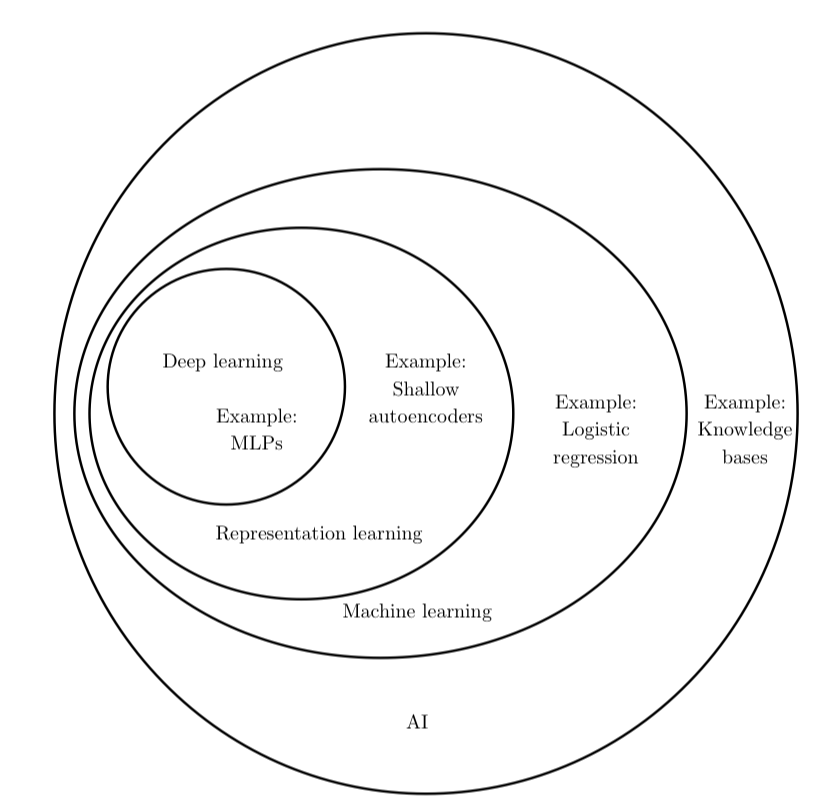
(深度学习和AI的关系,图片来源自花书)
深度学习模型分析和模型建立
这里我展示的是一个基于机器学习的模型:手写数字识别。我们可以在画板上手写0-9这十个数字,然后机器会将识别的结果反馈给你。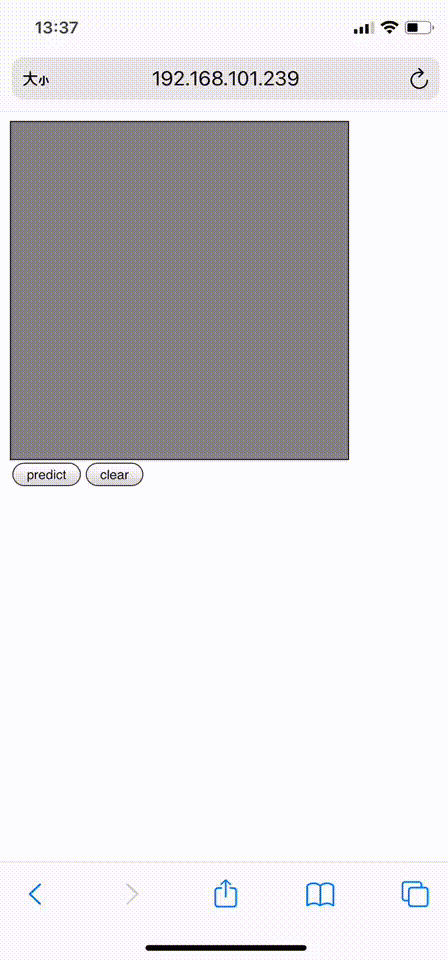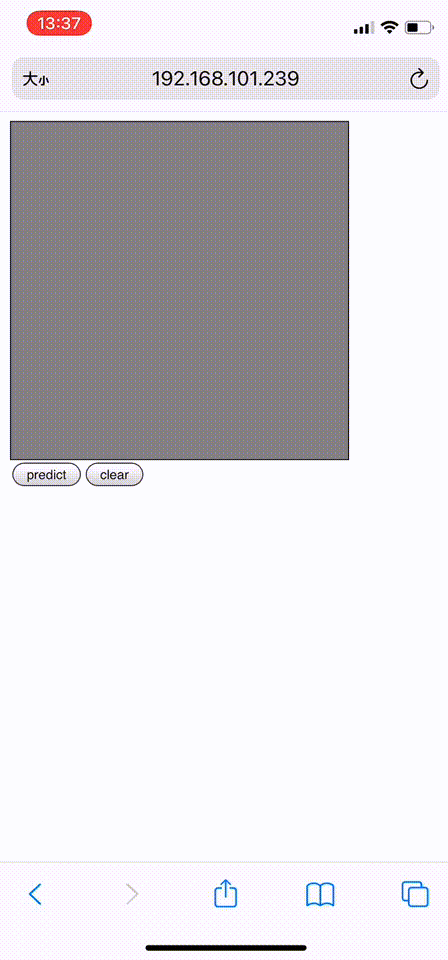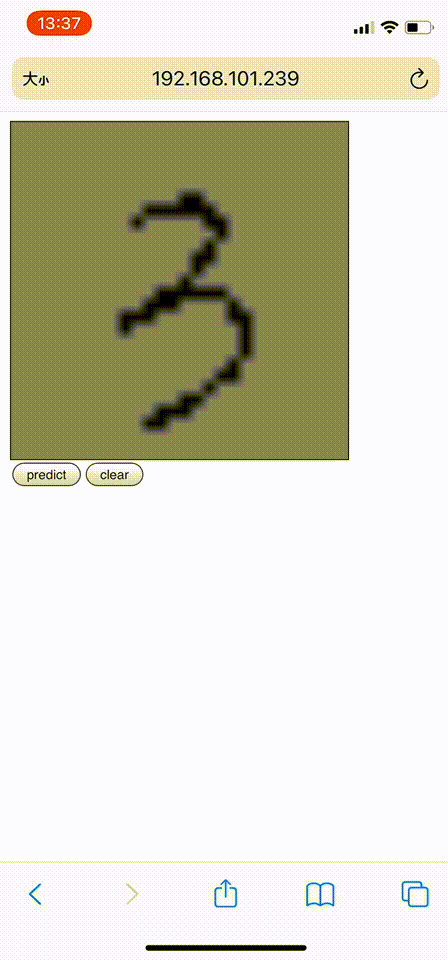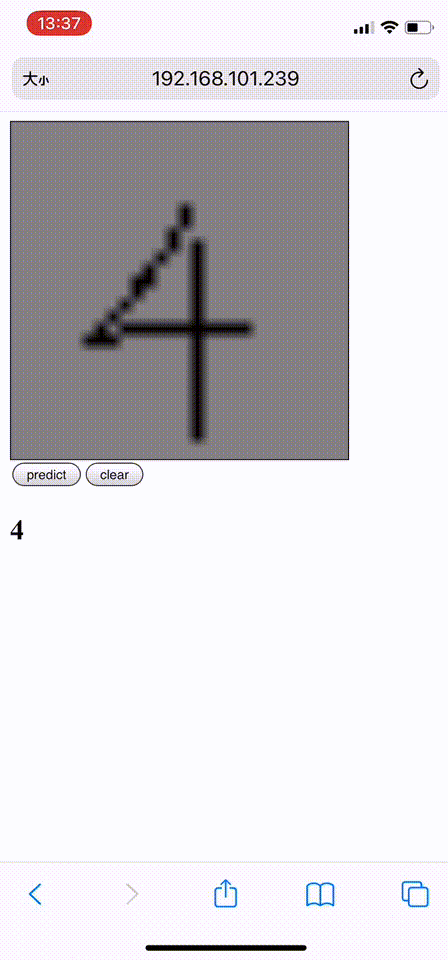
(为了更接近手写效果,用手机进行手写测试)
我们常规的编程技术肯定是无法解决这个问题的,因为我们是面对既定的输入,实现固定的输出(硬编码)。为了实现这个效果,这里展示一个经典的深度学习模型: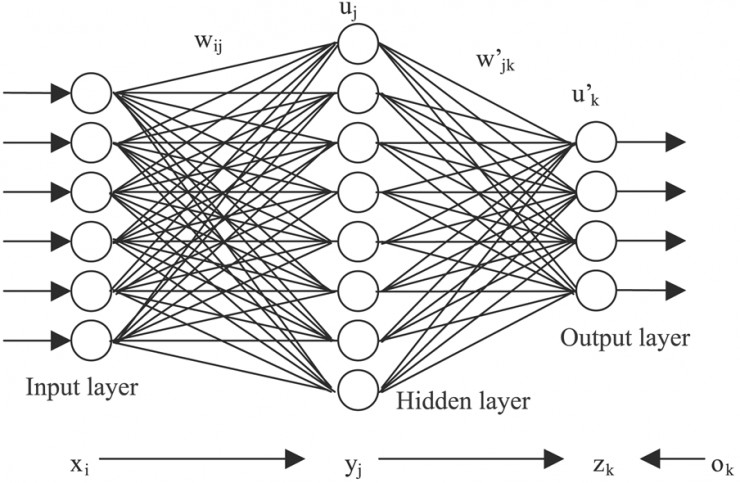
这种图形是很经典的深度学习模型,基本任何讲解这类知识的文章和视频都会展示这种图片。这张图片隐藏着以下的关键信息:
- 输入层(Input layer):数据输入,具有6个输入。
- 输出层(Output layer):结果输出,具有4个输出。
- 隐藏层(Hidden layer):隐藏层,主要的运算过程都会在隐藏层实现。之所以叫隐藏层是因为在这部分可以隐藏着很多的中间计算过程,为了简化模型,一般叫隐藏层。隐藏层在整个深度学习神经网络中可以看作一个黑盒,我们的重点在于关注一个输入会得到什么样的输出结果。这里的隐藏层具有8个节点。
- 正向传播:为什么叫神经网络,是因为每一层的结果都会被传递到下一个层处理,然后下一层继续向后传播。
在这个简单的手写数字模型中,我们用实际情况来实现一个神经网络模型:
- 输入层:采用一个28*28的矩阵表达一个图片,将图片拼接为一行,则输入层具有784个节点。
- 输出层:这个神经网络的目的是获得该模型对手写的0-9的数字的预测结果,所以具有10个节点,分别为0、1、2、3…、9。
- 隐藏层:为了简化模型,不使用任何隐藏层。
以上是这个深度学习的简化模型,接下来我们要去理解其数学表达、训练过程和一些术语。
模型的数学表达
为了表达我们的模型,只需要了解以下简单的概念:
输入:该模型的输入为7841的矩阵,也就是[1,2,3,4,5…(共784个)]。
输出:该模型的输出为101的矩阵,也就是[1,2,3…(共10个)]。
数学表达如下:
输入层:l=A(data+b)
| 变量 | l | A | data | b |
|---|---|---|---|---|
| 涵义 | 输入层的输出 | 激活函数 | 输入的数据 | 输入数据加权 |
| 矩阵结构/函数 | 1*784 | tanh | 1*784 | 1*784 |
输出层:output=A’(l·w+b)
| 变量 | output | A’ | l | w | b |
|---|---|---|---|---|---|
| 涵义 | 输出层的输出 | 激活函数 | 输入层输入的数据 | 输入数据加权 | |
| 矩阵结构/函数 | 1*10 | softmax | 1*784 | 784*10 | 1*10 |
在数学层面,所谓的正向传播,就是将某一层的输出作为下一层的输入。
在这个模型中,有三个变量,分别用红色标注起来。这三个变量决定了输入对应的输出结果。也就是说,我们所谓的「模型」是由bwb确定的。训练过程就是寻找解决该问题的最优bwb。这个寻找最优的过程称之为学习。而这个学习过程是机器自动完成的,所以也称为机器学习。
训练过程和数学关联
简单地来讲,一个训练过程是这样的:
图上包含了以下的信息:
- 模型是由各层定义的
- 一次训练过程是对一个模型输入数据,然后计算误差函数,再将误差作用到模型本身。
- 训练的目的就是为了减少误差,最终达到一个很好的预测结果。
用通俗的话讲,假设我们要开一家炸鸡店,要做最好的炸鸡。决定炸鸡口味的因素(也就是炸鸡的模型)有“材质”、“面粉厚度”、“油炸时间”。我们不断得制作炸鸡,客人品尝后进行“打分”,我们根据客人的“面粉太厚了”、“炸得太老了”等等评价来优化我们的炸鸡“模型”。从而逼近“最好的炸鸡”这个结果。
误差函数:
误差函数的意义为当前训练的预测结果和最优结果之间的差(方差或者平均差)。
在本例中,我们的输出为10*1的矩阵,表示对输入的值进行预测,其在0-9之间的分布结果。最优结果我们当然希望机器可以100%确定是0-9之间的某个值,例如:
[0,0,0,1,0,0,0,0,0,0]则表示机器可以确定值为3的概率为100%,其他为值的概率为0。
而我们实际某一步得到的预测值可能是这样的:
[0.23,0.11,0.40,0.001,0.22,0.22,0.12,0.11,0.3,0.2](随机写的,总和不一定为1);
这表示输入的值是0-9的可能性都存在,而为2的概率最大,为0.40,所以预测为2。
因此,我们就可以得到最优结果和预测结果直接的差值,假设使用y表示最优结果,y表示当前训练的结果,那么误差函数可以表示为:
L = (y - y)
(由于y包含0-9的预测结果,所以实际上L为:L = L+L+… = (y-y)+(y-y)+….)
而对于整体训练过程如果用P来表示一步时的模型参数(Model Parameters),则我们的目标为不断根据误差优化模型参数:
P -> P - k▽L
其中k表示学习率,可以理解为逼近的大小,如果学习率过大,是无法得到最优解的。
▽表示梯度,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大。
以上是对机器学习的过程的总结和数学关联,而其中主要难度在于求导数阶段,其他都是比较好理解的。
总结
深度学习的过程就是一个建立模型、初始化参数、正向传播和反向传播的过程,使机器根据数据集逐步优化自身,达到具有识别能力的过程。
Github: 手写数字识别学习模型的JS实现
(原up是用python实现的,这里我用了ml-matrix库重新实现,方便熟悉js的coder学习)
Bilibili: 弱鸡才用tensorflow,强者一个numpy就够:从零开始神经网络第一期

