二叉树的顺序存储结构（无师自通）

顺序存储只适用于完全二叉树，因此，如果我们想顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树

有读者会说，满二叉树也可以使用顺序存储。要知道，满二叉树也是完全二叉树，因为它满足完全二叉树的所有特征

普通二叉树转完全二叉树的方法很简单，只需给二叉树额外添加一些节点，将其”拼凑”成完全二叉树即可，如下图：

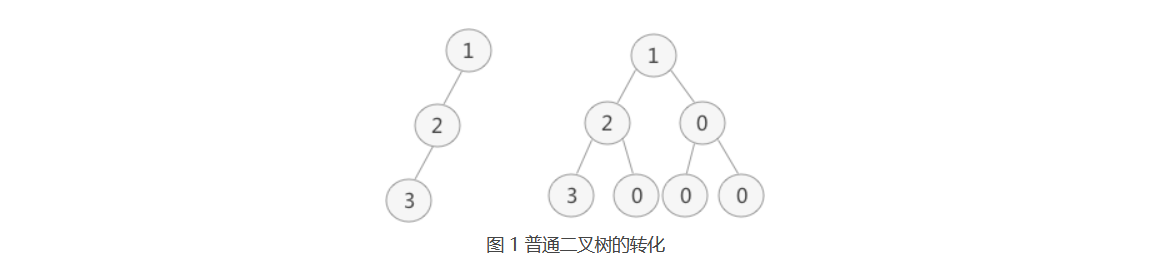
左侧是普通二叉树，右侧是转化后的完全（满）二叉树

完全二叉树的顺序存储，仅需从根节点开始，按照层次依次将树中节点存储到数组即可。

![%%ZH10%54%E38RAEU4OVYX.gif
图 2 完全二叉树示意图

例如，存储图 2 所示的完全二叉树，其存储状态如图 3 所示：

图 3 完全二叉树存储状态示意图

同样，存储由普通二叉树转化来的完全二叉树也是如此。例如，图 1 中普通二叉树的数组存储状态如图 4 所示：

图 4 普通二叉树的存储状态

由此，我们就实现了完全二叉树的顺序存储。

不仅如此，从顺序表中还原完全二叉树也很简单。我们知道，完全二叉树具有这样的性质，将树中节点按照层次并从左到右依次标号（1,2,3,…），若节点 i 有左右孩子，则其左孩子节点为 2i，右孩子节点为 2i+1。此性质可用于还原数组中存储的完全二叉树，也就是实现由图 3 到图 2、由图 4 到图 1 的转变。

二叉树的链式存储结构及（C语言）实现

因为并不是每个二叉树都是完全二叉树，普通二叉树使用顺序表存储或多或多会存在空间浪费的现象

所以本节我们来学习链式存储结构

本节我们学习二叉树的链式存储结构。

O]TCV79LT2NNKJNV@WU@NLT.gif
图 1 普通二叉树示意图

如图 1 所示，此为一棵普通的二叉树，若将其采用链式存储，则只需从树的根节点开始，将各个节点及其左右孩子使用链表存储即可。因此，图 1 对应的链式存储结构如图 2 所示：

8W(A{L5@5YKDSP417J$F]`E.gif
图 2 二叉树链式存储结构示意图

由图 2 可知，采用链式存储二叉树时，其节点结构由 3 部分构成（如图 3 所示）：

指向左孩子节点的指针（Lchild）；
节点存储的数据（data）；
指向右孩子节点的指针（Rchild）；

$~T9{N_H8[64XD~S}]HGWKZO.gif$
图 3 二叉树节点结构

表示该节点结构的 C 语言代码为：

    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
        struct BiTNode *parent;
    }BiTNode,*BiTree;

图 2 中的链式存储结构对应的 C 语言代码为：

    #include <stdio.h>
    #include <stdlib.h>
    #define TElemType int
    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
    }BiTNode,*BiTree;
    void CreateBiTree(BiTree *T){
        *T=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data=1;
        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->data=2;
        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->data=3;
        (*T)->rchild->lchild=NULL;
        (*T)->rchild->rchild=NULL;
        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->lchild->data=4;
        (*T)->lchild->rchild=NULL;
        (*T)->lchild->lchild->lchild=NULL;
        (*T)->lchild->lchild->rchild=NULL;
    }
    int main() {
        BiTree Tree;
        CreateBiTree(&Tree);
        printf("%d",Tree->lchild->lchild->data);
        return 0;
    }

其实，二叉树的链式存储结构远不止图 2 所示的这一种。例如，在某些实际场景中，可能会做 “查找某节点的父节点” 的操作，这时可以在节点结构中再添加一个指针域，用于各个节点指向其父亲节点，如图 4 所示：
YXTEC@]MFLJ]{WB5RJL87W0.gif

图 4 自定义二叉树的链式存储结构
这样的链表结构，通常称为三叉链表。
利用图 4 所示的三叉链表，我们可以很轻松地找到各节点的父节点。因此，在解决实际问题时，用合适的链表结构存储二叉树，可以起到事半功倍的效果

浅谈二叉树的（4 种）遍历算法

二叉树先序遍历（递归与非递归）及C语言实现

先序遍历思想过程

访问根节点；
访问当前节点的左子树；
若当前节点无左子树，则访问当前节点的右子树；

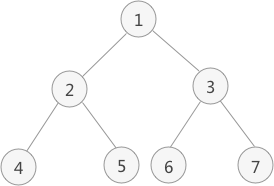
图 1 二叉树

以图 1 为例，采用先序遍历的思想遍历该二叉树的过程为：

访问该二叉树的根节点，找到 1；
访问节点 1 的左子树，找到节点 2；
访问节点 2 的左子树，找到节点 4；
由于访问节点 4 左子树失败，且也没有右子树，因此以节点 4 为根节点的子树遍历完成。但节点 2 还没有遍历其右子树，因此现在开始遍历，即访问节点 5；
由于节点 5 无左右子树，因此节点 5 遍历完成，并且由此以节点 2 为根节点的子树也遍历完成。现在回到节点 1 ，并开始遍历该节点的右子树，即访问节点 3；
访问节点 3 左子树，找到节点 6；
由于节点 6 无左右子树，因此节点 6 遍历完成，回到节点 3 并遍历其右子树，找到节点 7；
节点 7 无左右子树，因此以节点 3 为根节点的子树遍历完成，同时回归节点 1。由于节点 1 的左右子树全部遍历完成，因此整个二叉树遍历完成；

因此，图 1 中二叉树采用先序遍历得到的序列为：

1 2 4 5 3 6 7

递归实现

二叉树的先序遍历采用的是递归的思想，因此可以递归实现，其 C 语言实现代码为：

    #include <stdio.h>
    #include <string.h>
    #define TElemType int
    //构造结点的结构体
    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
    }BiTNode,*BiTree;
    //初始化树的函数
    void CreateBiTree(BiTree *T){
        *T=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data=1;
        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->data=2;
        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild->data=5;
        (*T)->lchild->rchild->lchild=NULL;
        (*T)->lchild->rchild->rchild=NULL;
        (*T)->rchild->data=3;
        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->lchild->data=6;
        (*T)->rchild->lchild->lchild=NULL;
        (*T)->rchild->lchild->rchild=NULL;
        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->rchild->data=7;
        (*T)->rchild->rchild->lchild=NULL;
        (*T)->rchild->rchild->rchild=NULL;
        (*T)->lchild->lchild->data=4;
        (*T)->lchild->lchild->lchild=NULL;
        (*T)->lchild->lchild->rchild=NULL;
    }
    //模拟操作结点元素的函数，输出结点本身的数值
    void displayElem(BiTNode* elem){
        printf("%d ",elem->data);
    }
    //先序遍历
    void PreOrderTraverse(BiTree T){
        if (T) {
            displayElem(T);//调用操作结点数据的函数方法
            PreOrderTraverse(T->lchild);//访问该结点的左孩子
            PreOrderTraverse(T->rchild);//访问该结点的右孩子
        }
        //如果结点为空，返回上一层
        return;
    }
    int main() {
        BiTree Tree;
        CreateBiTree(&Tree);
        printf("先序遍历: \n");
    }

非递归实现

而递归的底层实现依靠的是栈存储结构，因此，二叉树的先序遍历既可以直接采用递归思想实现，也可以使用栈的存储结构模拟递归的思想实现，其 C 语言实现代码为

    #include <stdio.h>
    #include <string.h>
    #define TElemType int
    int top=-1;//top变量时刻表示栈顶元素所在位置
    //构造结点的结构体
    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
    }BiTNode,*BiTree;
    //初始化树的函数
    void CreateBiTree(BiTree *T){
        *T=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data=1;
        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->data=2;
        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild->data=5;
        (*T)->lchild->rchild->lchild=NULL;
        (*T)->lchild->rchild->rchild=NULL;
        (*T)->rchild->data=3;
        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->lchild->data=6;
        (*T)->rchild->lchild->lchild=NULL;
        (*T)->rchild->lchild->rchild=NULL;
        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->rchild->data=7;
        (*T)->rchild->rchild->lchild=NULL;
        (*T)->rchild->rchild->rchild=NULL;
        (*T)->lchild->lchild->data=4;
        (*T)->lchild->lchild->lchild=NULL;
        (*T)->lchild->lchild->rchild=NULL;
    }
    //前序遍历使用的进栈函数
    void push(BiTNode** a,BiTNode* elem){
        a[++top]=elem;
    }
    //弹栈函数
    void pop( ){
        if (top==-1) {
            return ;
        }
        top--;
    }
    //模拟操作结点元素的函数，输出结点本身的数值
    void displayElem(BiTNode* elem){
        printf("%d ",elem->data);
    }
    //拿到栈顶元素
    BiTNode* getTop(BiTNode**a){
        return a[top];
    }
    //先序遍历非递归算法
    void PreOrderTraverse(BiTree Tree){
        BiTNode* a[20];//定义一个顺序栈
        BiTNode * p;//临时指针
        push(a, Tree);//根结点进栈
        while (top!=-1) {
            p=getTop(a);//取栈顶元素
            pop();//弹栈
            while (p) {
                displayElem(p);//调用结点的操作函数
                //如果该结点有右孩子，右孩子进栈
                if (p->rchild) {
                    push(a,p->rchild);
                }
                p=p->lchild;//一直指向根结点最后一个左孩子
            }
        }
    }
    int main(){
        BiTree Tree;
        CreateBiTree(&Tree);
        printf("先序遍历: \n");
        PreOrderTraverse(Tree);
    }

二叉树中序遍历（递归和非递归）算法及C语言实现

中序遍历思想过程

访问当前节点的左子树；
访问根节点；
访问当前节点的右子树；

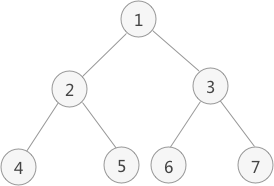
图 1 二叉树

以图 1 为例，采用中序遍历的思想遍历该二叉树的过程为：

访问该二叉树的根节点，找到 1；
遍历节点 1 的左子树，找到节点 2；
遍历节点 2 的左子树，找到节点 4；
由于节点 4 无左孩子，因此找到节点 4，并遍历节点 4 的右子树；
由于节点 4 无右子树，因此节点 2 的左子树遍历完成，访问节点 2；
遍历节点 2 的右子树，找到节点 5；
由于节点 5 无左子树，因此访问节点 5 ，又因为节点 5 没有右子树，因此节点 1 的左子树遍历完成，访问节点 1 ，并遍历节点 1 的右子树，找到节点 3；
遍历节点 3 的左子树，找到节点 6；
由于节点 6 无左子树，因此访问节点 6，又因为该节点无右子树，因此节点 3 的左子树遍历完成，开始访问节点 3 ，并遍历节点 3 的右子树，找到节点 7；
由于节点 7 无左子树，因此访问节点 7，又因为该节点无右子树，因此节点 1 的右子树遍历完成，即整棵树遍历完成；

因此，图 1 中二叉树采用中序遍历得到的序列为：

4 2 5 1 6 3 7

递归实现

二叉树的中序遍历采用的是递归的思想，因此可以递归实现，其 C 语言实现代码为：

    #include <stdio.h>
    #include <string.h>
    #define TElemType int
    //构造结点的结构体
    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
    }BiTNode,*BiTree;
    //初始化树的函数
    void CreateBiTree(BiTree *T){
        *T=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data=1;
        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->data=2;
        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild->data=5;
        (*T)->lchild->rchild->lchild=NULL;
        (*T)->lchild->rchild->rchild=NULL;
        (*T)->rchild->data=3;
        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->lchild->data=6;
        (*T)->rchild->lchild->lchild=NULL;
        (*T)->rchild->lchild->rchild=NULL;
        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->rchild->data=7;
        (*T)->rchild->rchild->lchild=NULL;
        (*T)->rchild->rchild->rchild=NULL;
        (*T)->lchild->lchild->data=4;
        (*T)->lchild->lchild->lchild=NULL;
        (*T)->lchild->lchild->rchild=NULL;
    }
    //模拟操作结点元素的函数，输出结点本身的数值
    void displayElem(BiTNode* elem){
        printf("%d ",elem->data);
    }
    //中序遍历
    void INOrderTraverse(BiTree T){
        if (T) {
            INOrderTraverse(T->lchild);//遍历左孩子
            displayElem(T);//调用操作结点数据的函数方法
            INOrderTraverse(T->rchild);//遍历右孩子
        }
        //如果结点为空，返回上一层
        return;
    }
    int main() {
        BiTree Tree;
        CreateBiTree(&Tree);
        printf("中序遍历算法: \n");
        INOrderTraverse(Tree);
    }

非递归实现

而递归的底层实现依靠的是栈存储结构，因此，二叉树的先序遍历既可以直接采用递归思想实现，也可以使用栈的存储结构模拟递归的思想实现。

中序遍历的非递归方式实现思想是：从根结点开始，遍历左孩子同时压栈，当遍历结束，说明当前遍历的结点没有左孩子，从栈中取出来调用操作函数，然后访问该结点的右孩子，继续以上重复性的操作。

除此之外，还有另一种实现思想：中序遍历过程中，只需将每个结点的左子树压栈即可，右子树不需要压栈。当结点的左子树遍历完成后，只需要以栈顶结点的右孩子为根结点，继续循环遍历即可。

两种非递归方法实现二叉树中序遍历的代码实现为：

    #include <stdio.h>
    #include <string.h>
    #define TElemType int
    int top=-1;//top变量时刻表示栈顶元素所在位置
    //构造结点的结构体
    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
    }BiTNode,*BiTree;
    //初始化树的函数
    void CreateBiTree(BiTree *T){
        *T=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data=1;
        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->data=2;
        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild->data=5;
        (*T)->lchild->rchild->lchild=NULL;
        (*T)->lchild->rchild->rchild=NULL;
        (*T)->rchild->data=3;
        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->lchild->data=6;
        (*T)->rchild->lchild->lchild=NULL;
        (*T)->rchild->lchild->rchild=NULL;
        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->rchild->data=7;
        (*T)->rchild->rchild->lchild=NULL;
        (*T)->rchild->rchild->rchild=NULL;
        (*T)->lchild->lchild->data=4;
        (*T)->lchild->lchild->lchild=NULL;
        (*T)->lchild->lchild->rchild=NULL;
    }
    //前序和中序遍历使用的进栈函数
    void push(BiTNode** a,BiTNode* elem){
        a[++top]=elem;
    }
    //弹栈函数
    void pop( ){
        if (top==-1) {
            return ;
        }
        top--;
    }
    //模拟操作结点元素的函数，输出结点本身的数值
    void displayElem(BiTNode* elem){
        printf("%d ",elem->data);
    }
    //拿到栈顶元素
    BiTNode* getTop(BiTNode**a){
        return a[top];
    }
    //中序遍历非递归算法
    void InOrderTraverse1(BiTree Tree){
        BiTNode* a[20];//定义一个顺序栈
        BiTNode * p;//临时指针
        push(a, Tree);//根结点进栈
        while (top!=-1) {//top!=-1说明栈内不为空，程序继续运行
            while ((p=getTop(a)) &&p){//取栈顶元素，且不能为NULL
                push(a, p->lchild);//将该结点的左孩子进栈，如果没有左孩子，NULL进栈
            }
            pop();//跳出循环，栈顶元素肯定为NULL，将NULL弹栈
            if (top!=-1) {
                p=getTop(a);//取栈顶元素
                pop();//栈顶元素弹栈
                displayElem(p);
                push(a, p->rchild);//将p指向的结点的右孩子进栈
            }
        }
    }
    //中序遍历实现的另一种方法
    void InOrderTraverse2(BiTree Tree){
        BiTNode* a[20];//定义一个顺序栈
        BiTNode * p;//临时指针
        p=Tree;
        //当p为NULL或者栈为空时，表明树遍历完成
        while (p || top!=-1) {
            //如果p不为NULL，将其压栈并遍历其左子树
            if (p) {
                push(a, p);
                p=p->lchild;
            }
            //如果p==NULL，表明左子树遍历完成，需要遍历上一层结点的右子树
            else{
                p=getTop(a);
                pop();
                displayElem(p);
                p=p->rchild;
            }
        }
    }
    int main(){
        BiTree Tree;
        CreateBiTree(&Tree);
        printf("\n中序遍历算法1: \n");
        InOrderTraverse1(Tree);
        printf("\n中序遍历算法2: \n");
        InOrderTraverse2(Tree);
    }

二叉树后序遍历（递归与非递归）算法及C语言实现

后序遍历的实现思想

从根节点出发，依次遍历各节点的左右子树，直到当前节点左右子树遍历完成后，才访问该节点元素。

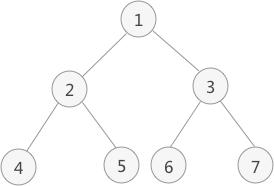
图 1 二叉树

如图 1 中，对此二叉树进行后序遍历的操作过程为：

从根节点 1 开始，遍历该节点的左子树（以节点 2 为根节点）；
遍历节点 2 的左子树（以节点 4 为根节点）；
由于节点 4 既没有左子树，也没有右子树，此时访问该节点中的元素 4，并回退到节点 2 ，遍历节点 2 的右子树（以 5 为根节点）；
由于节点 5 无左右子树，因此可以访问节点 5 ，并且此时节点 2 的左右子树也遍历完成，因此也可以访问节点 2；
此时回退到节点 1 ，开始遍历节点 1 的右子树（以节点 3 为根节点）；
遍历节点 3 的左子树（以节点 6 为根节点）；
由于节点 6 无左右子树，因此访问节点 6，并回退到节点 3，开始遍历节点 3 的右子树（以节点 7 为根节点）；
由于节点 7 无左右子树，因此访问节点 7，并且节点 3 的左右子树也遍历完成，可以访问节点 3；节点 1 的左右子树也遍历完成，可以访问节点 1；
到此，整棵树的遍历结束。

由此，对图 1 中二叉树进行后序遍历的结果为：

4 5 2 6 7 3 1

递归实现
后序遍历的递归实现代码为：

    #include <stdio.h>
    #include <string.h>
    #define TElemType int
    //构造结点的结构体
    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
    }BiTNode,*BiTree;
    //初始化树的函数
    void CreateBiTree(BiTree *T){
        *T=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data=1;
        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));

        (*T)->lchild->data=2;
        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild->data=5;
        (*T)->lchild->rchild->lchild=NULL;
        (*T)->lchild->rchild->rchild=NULL;
        (*T)->rchild->data=3;
        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->lchild->data=6;
        (*T)->rchild->lchild->lchild=NULL;
        (*T)->rchild->lchild->rchild=NULL;
        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->rchild->data=7;
        (*T)->rchild->rchild->lchild=NULL;
        (*T)->rchild->rchild->rchild=NULL;
        (*T)->lchild->lchild->data=4;
        (*T)->lchild->lchild->lchild=NULL;
        (*T)->lchild->lchild->rchild=NULL;
    }
    //模拟操作结点元素的函数，输出结点本身的数值
    void displayElem(BiTNode* elem){
        printf("%d ",elem->data);
    }
    //后序遍历
    void PostOrderTraverse(BiTree T){
        if (T) {
            PostOrderTraverse(T->lchild);//遍历左孩子
            PostOrderTraverse(T->rchild);//遍历右孩子
            displayElem(T);//调用操作结点数据的函数方法
        }
        //如果结点为空，返回上一层
        return;
    }
    int main() {
        BiTree Tree;
        CreateBiTree(&Tree);
        printf("后序遍历: \n");
        PostOrderTraverse(Tree);
    }

非递归实现

递归算法底层的实现使用的是栈存储结构，所以可以直接使用栈写出相应的非递归算法。

后序遍历是在遍历完当前结点的左右孩子之后，才调用操作函数，所以需要在操作结点进栈时，为每个结点配备一个标志位。当遍历该结点的左孩子时，设置当前结点的标志位为 0，进栈；当要遍历该结点的右孩子时，设置当前结点的标志位为 1，进栈。

这样，当遍历完成，该结点弹栈时，查看该结点的标志位的值：如果是 0，表示该结点的右孩子还没有遍历；反之如果是 1，说明该结点的左右孩子都遍历完成，可以调用操作函数。

完整实现代码为：

    #include <stdio.h>
    #include <string.h>
    #define TElemType int
    int top=-1;//top变量时刻表示栈顶元素所在位置
    //构造结点的结构体
    typedef struct BiTNode{
        TElemType data;//数据域
        struct BiTNode *lchild,*rchild;//左右孩子指针
    }BiTNode,*BiTree;
    //初始化树的函数
    void CreateBiTree(BiTree *T){
        *T=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->data=1;
        (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->data=2;
        (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->lchild->rchild->data=5;
        (*T)->lchild->rchild->lchild=NULL;
        (*T)->lchild->rchild->rchild=NULL;
        (*T)->rchild->data=3;
        (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->lchild->data=6;
        (*T)->rchild->lchild->lchild=NULL;
        (*T)->rchild->lchild->rchild=NULL;
        (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
        (*T)->rchild->rchild->data=7;
        (*T)->rchild->rchild->lchild=NULL;
        (*T)->rchild->rchild->rchild=NULL;
        (*T)->lchild->lchild->data=4;
        (*T)->lchild->lchild->lchild=NULL;
        (*T)->lchild->lchild->rchild=NULL;
    }
    //弹栈函数
    void pop( ){
        if (top==-1) {
            return ;
        }
        top--;
    }
    //模拟操作结点元素的函数，输出结点本身的数值
    void displayElem(BiTNode* elem){
        printf("%d ",elem->data);
    }
    //后序遍历非递归算法
    typedef struct SNode{
        BiTree p;
        int tag;
    }SNode;
    //后序遍历使用的进栈函数
    void postpush(SNode *a,SNode sdata){
        a[++top]=sdata;
    }
    //后序遍历函数
    void PostOrderTraverse(BiTree Tree){
        SNode a[20];//定义一个顺序栈
        BiTNode * p;//临时指针
        int tag;
        SNode sdata;
        p=Tree;
        while (p||top!=-1) {
            while (p) {
                //为该结点入栈做准备
                sdata.p=p;
                sdata.tag=0;//由于遍历是左孩子，设置标志位为0
                postpush(a, sdata);//压栈
                p=p->lchild;//以该结点为根结点，遍历左孩子
            }
            sdata=a[top];//取栈顶元素
            pop();//栈顶元素弹栈
            p=sdata.p;
            tag=sdata.tag;
            //如果tag==0，说明该结点还没有遍历它的右孩子
            if (tag==0) {
                sdata.p=p;
                sdata.tag=1;
                postpush(a, sdata);//更改该结点的标志位，重新压栈
                p=p->rchild;//以该结点的右孩子为根结点，重复循环
            }
            //如果取出来的栈顶元素的tag==1，说明此结点左右子树都遍历完了，可以调用操作函数了
            else{
                displayElem(p);
                p=NULL;
            }
        }
    }
    int main(){
        BiTree Tree;
        CreateBiTree(&Tree);
        printf("后序遍历: \n");
        PostOrderTraverse(Tree);
    }

二叉树层次遍历及其C语言实现

PTA例题

求二叉树高度



int GetHeight( BinTree BT ){
    if(BT==NULL)return 0;    //先判断树是否有根节点，即是否为空
    int x,y;
    x=GetHeight(BT->Left)+1;    
    y=GetHeight(BT->Right)+1;
    return x>y?x:y;
}

二叉树的遍历

#define MAXSIZE 50
void InorderTraversal( BinTree BT )//中序遍历 左根右 
{
 if(BT)
 {
  InorderTraversal(BT->Left);
  printf(" %c",BT->Data);
  InorderTraversal(BT->Right); 
 }
 } 
 void PreorderTraversal( BinTree BT )//先序遍历(根左右)
 {
  if(BT){
       printf(" %c",BT->Data);
       PreorderTraversal(BT->Left);
       PreorderTraversal(BT->Right);
    }
  } 
void PostorderTraversal( BinTree BT )//后序  左右根 
{
 if(BT)
 {
      PostorderTraversal(BT->Left);
      PostorderTraversal(BT->Right);
      printf(" %c",BT->Data);
   }
}  
void LevelorderTraversal( BinTree BT )//第一种方法，若实现需要加上一些函数
{
 Queue Q;
 BinTree T;

 if(!BT) return ;

 Q = CreatQueue();
 AddQ(Q, BT);

 while(!IsEmpty(Q))
       {
      T = DeleteQ(Q);
      printf(" %c",T->Data);
      if(T->Left)  AddQ(Q,T->Left);
      if(T->Right) AddQ(Q,T->Right);
    }
} 
/*void LevelorderTraversal( BinTree BT )//remember!!!我自己比较喜欢的方法
{    
    if(BT == NULL) return;        
    BinTree s[MAXSIZE];        
    int front,rear;    
    front = rear = -1;        
    s[++rear] = BT;//根指针入队         
    while(front!=rear){        
        front = (front+1)%MAXSIZE;        
        BinTree q = s[front];//队列的头元素出队         
        printf(" %c", q->Data);                
        if(q->Left){            
        rear = (rear+1)%MAXSIZE;            
        s[rear]=q->Left;//若q有左孩子，则左孩子指针入队         
        }        
        if(q->Right){            
        rear =(rear+1)%MAXSIZE;            
        s[rear]=q->Right;//若右有左孩子，则右孩子指针入队         
        }    
    } 
}  
*/

先序输出叶结点

void PreorderPrintLeaves( BinTree BT )
{
    if(BT == NULL){    //判断数是否为空
        return;
    }
    if(BT->Left == NULL && BT->Right == NULL){    //判断是否为叶节点的条件，即所在节点的左右节点是否为空，
        printf(" %c",BT->Data);
    }
    PreorderPrintLeaves(BT->Left);    //遍历左子树
    PreorderPrintLeaves(BT->Right); //遍历右子树
}

根据后序和中序遍历输出先序遍历


#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
typedef struct BiNode
{
    int data;
    struct BiNode *lchild;
    struct BiNode *rchild;
}BiNode, *BiTree;
BiTree BuildPreTree(int *End, int *Mid, int n)//根据后序和中序构造二叉树
{
    if(n <= 0)
        return NULL;
    int *p = Mid;
    while(*p != *(End+n-1))//后序的最后一个数是根节点，将p移动到中序的根节点位置，p就将中序分成左子树部分和右子树部分
          p++;
    BiTree T;
    T = (BiNode*)malloc(sizeof(BiNode));
    T->data = *p;
    int len_l = p - Mid;
    T->lchild = BuildPreTree(End, Mid, len_l);//找到左子树根节点，递归
    T->rchild = BuildPreTree(End+len_l, Mid+len_l+1, n-len_l-1);
    return T;
}
void CoutPre(BiTree T)//先序输出
{
    if( T != NULL ){
        printf(" %d", T->data);
        CoutPre(T->lchild);
        CoutPre(T->rchild);
    }

}
int main()
{
    int N, *End, *Mid;
    scanf("%d", &N);
    End = (int*)malloc(sizeof(int)*N);
    Mid = (int*)malloc(sizeof(int)*N);
    for(int i=0; i<N; i++)
        scanf("%d", &End[i]);
    for(int i=0; i<N; i++)
        scanf("%d", &Mid[i]);
    BiTree T = BuildPreTree(End, Mid, N);
    printf("Preorder:");
    CoutPre(T);
}


/*先根据后序和中序得出那个二叉树，然后再输出
使用递归来对树进行赋值。后序序列中最后一个元素为根,
中序序列中该结点前的元素为左子树,后的元素为右子树。
对于左/右子树,最后一个在后序序列中出现的元素为子树的根结点,
再看中序序列,依此类推
主要的是怎么后序序列中找子树的根节点,递归中也要求子树的长度来求最后位置的那个根结点
*/

数据结构（C语言版）

08--树

二叉树的顺序存储结构（无师自通）

二叉树的链式存储结构及（C语言）实现

浅谈二叉树的（4 种）遍历算法

二叉树先序遍历（递归与非递归）及C语言实现

递归实现

非递归实现

二叉树中序遍历（递归和非递归）算法及C语言实现

递归实现

非递归实现

二叉树后序遍历（递归与非递归）算法及C语言实现

递归实现

非递归实现

二叉树层次遍历及其C语言实现

PTA例题

求二叉树高度

二叉树的遍历

先序输出叶结点

根据后序和中序遍历输出先序遍历