种质资源研究文献

由来： 王海岗, 贾冠清, 智慧, 温琪汾, 董俊丽, 陈凌, 王君杰, 曹晓宁, 刘思辰, 王纶, 乔治军, 刁现民. . 谷子核心种质表型遗传多样性分析及综合评价. 作物学报, 2015, 42(1): 19-30
1.3 数据分析（感觉文中没有应用这个模糊隶属函数，有可能就是多讲了一句话，实际是在说计算Shannon-Wiener diversity index，不过文章的分析思路值得学习）
采用Microsoft Excel 2003和Statistic 6.0整理和分析数据。采用DPS7.05进行聚类分析、相关分析和主成分分析, 并计算各主成分得分及综合得分, 再结合逐步回归分析筛选谷子资源综合性状评价指标。采用模糊隶属函数计算出各性状的隶属函数值, μ (xi)=(xi-xi_min)/(_xi_max-_xi_min) (_i=1, 2, 3, …, 878), 即将各性状定义到[0, 1]闭区间。式中, μ (xi)为某种质材料第i个性状的隶属函数值, xi为某种质材料的第i个性状值, xi_max、_xi_min分别为所有种质资源中第_i个性状的最大值和最小值。采用Shannon-Wiener’ s多样性指数(Shannon-Wiener diversity index, H‘)进行遗传多样性评价。

部分概念的解读

Definition：
若对论域（研究的范围）U中的任一元素x，都有一个数A(x)∈[0，1]与之对应，则称A为U上的模糊集，A(x )称为x对A的隶属度。当x在U中变动时，A( x)就是一个函数，称为A的隶属函数。隶属度A(x)越接近于1，表示x属于A的程度越高，A(x)越接近于0表示x属于A的程度越低。用取值于区间(0，1)的隶属函数A(x)表征x 属于A的程度高低。隶属度属于模糊评价函数里的概念：模糊综合评价是对受多种因素影响的事物做出全面评价的一种十分有效的多因素决策方法，其特点是评价结果不是绝对地肯定或否定，而是以一个模糊集合来表示。
Example：
A(x )=表示模糊集“年老”的隶属函数，A表示模糊集“年老”，当年龄x≤50时A（x）=0表明x不属于模糊集A（即“年老”），当x ≥100时，A（x）=1表明x 完全属于A，当50以下是更为专业的参考资料：
第4 章隶属函数的确定方法.pdf

模糊关系及其计算

一般情况是先将数据按行为样品列为参数整理成2维表，然后运用百分均值思想将值全部转化为0-1之间的数据。
模糊矩阵的合成类似于普通矩阵的乘积运算，将乘积运算换成“取小”，将加法运算换成“取大”即可。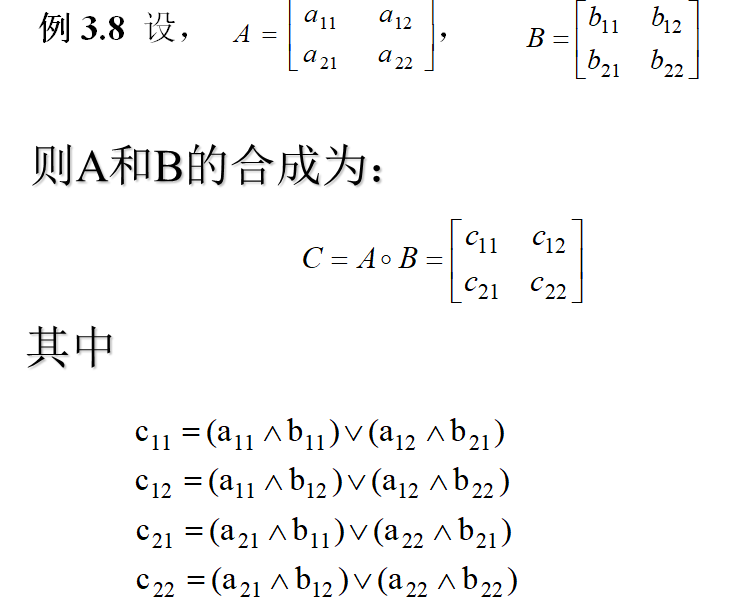



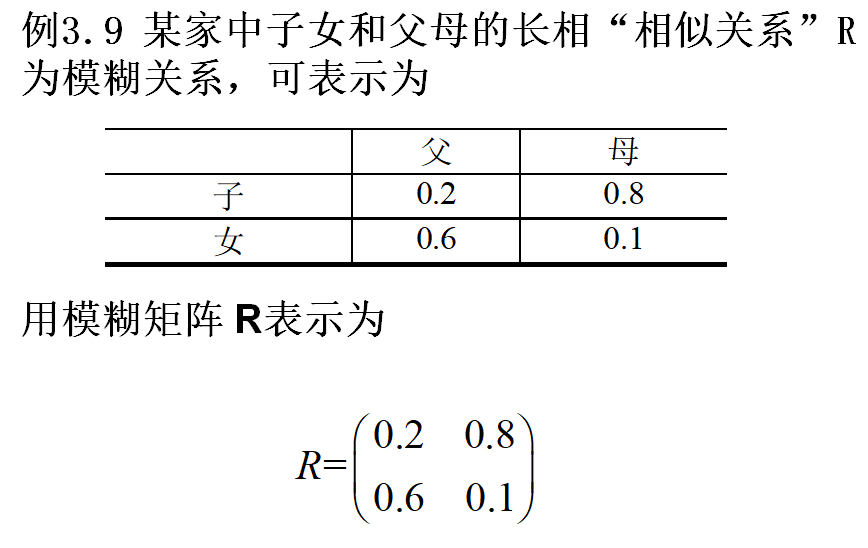
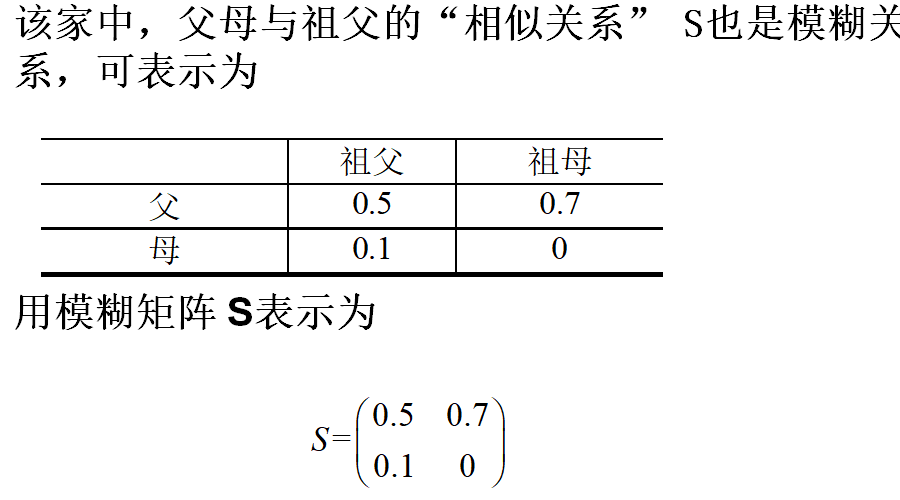
实际运算过程中就是针对每个值取小、取小，再取大的结果。例如0.2的由来就是先0.2与0.5取小为0.2，再0.8与0.1取小为0.1，然后0.2与0.1取大为0.2.