一、运算符优先级&转义字符

括号强转 > 自增自减 > 地址 > 逻辑非(感叹号) > 乘除取余 > 加减 > 移位 > 比较 > 等于(==、!=)
> 位运算(& ^ |) > 逻辑运算(&& || ) > 条件(?:) > 赋值

优先级 运算符 名称或含义 使用形式 结合方向 说明
1 [] 数组下标 数组名[常量表达式] 左到右

| | | () | 圆括号 | （表达式）/函数名(形参表) | |

| | | . | 成员选择（对象） | 对象.成员名 | |

| | | -> | 成员选择（指针） | 对象指针->成员名 | |

| | 2 | - | 负号运算符 | -表达式 | 右到左 | 单目运算符 | | | (类型) | 强制类型转换 | (数据类型)表达式 | |

| | | ++ | 前置自增运算符 | ++变量名 | | 单目运算符 | | | ++ | 后置自增运算符 | 变量名++ | | 单目运算符 | | | — | 前置自减运算符 | —变量名 | | 单目运算符 | | | — | 后置自减运算符 | 变量名— | | 单目运算符 | | | | 取值运算符 | 指针变量 | | 单目运算符 | | | & | 取地址运算符 | &变量名 | | 单目运算符 | | | ! | 逻辑非运算符 | !表达式 | | 单目运算符 | | | ~ | 按位取反运算符 | ~表达式 | | 单目运算符 | | | sizeof | 长度运算符 | sizeof(表达式) | |

| | 3 | / | 除 | 表达式/表达式 | 左到右 | 双目运算符 | | | | 乘 | 表达式表达式 | | 双目运算符 | | | % | 余数（取模） | 整型表达式/整型表达式 | | 双目运算符 | | 4 | + | 加 | 表达式+表达式 | 左到右 | 双目运算符 | | | - | 减 | 表达式-表达式 | | 双目运算符 | | 5 | << | 左移 | 变量 | 左到右 | 双目运算符 | | | >> | 右移 | 变量>>表达式 | | 双目运算符 | | 6 | > | 大于 | 表达式>表达式 | 左到右 | 双目运算符 | | | >= | 大于等于 | 表达式>=表达式 | | 双目运算符 | | | < | 小于 | 表达式 | | 双目运算符 | | | <= | 小于等于 | 表达式 | | 双目运算符 | | 7 | == | 等于 | 表达式==表达式 | 左到右 | 双目运算符 | | | != | 不等于 | 表达式!= 表达式 | | 双目运算符 | | 8 | & | 按位与 | 表达式&表达式 | 左到右 | 双目运算符 | | 9 | ^ | 按位异或 | 表达式^表达式 | 左到右 | 双目运算符 | | 10 | | | 按位或 | 表达式|表达式 | 左到右 | 双目运算符 | | 11 | && | 逻辑与 | 表达式&&表达式 | 左到右 | 双目运算符 | | 12 | || | 逻辑或 | 表达式||表达式 | 左到右 | 双目运算符 | | 13 | ?: | 条件运算符 | 表达式1? 表达式2: 表达式3 | 右到左 | 三目运算符 | | 14 | = | 赋值运算符 | 变量=表达式 | 右到左 |

| | | /= | 除后赋值 | 变量/=表达式 | |

| | | = | 乘后赋值 | 变量=表达式 | |

| | | %= | 取模后赋值 | 变量%=表达式 | |

| | | += | 加后赋值 | 变量+=表达式 | |

| | | -= | 减后赋值 | 变量-=表达式 | |

| | | <<= | 左移后赋值 | 变量<<=表达式 | |

| | | >>= | 右移后赋值 | 变量>>=表达式 | |

| | | &= | 按位与后赋值 | 变量&=表达式 | |

| | | ^= | 按位异或后赋值 | 变量^=表达式 | |

| | | |= | 按位或后赋值 | 变量|=表达式 | |

| | 15 | , | 逗号运算符 | 表达式,表达式,… | 左到右 | 从左向右顺序运算 |

转义字符 含义 ASCII码值
\n 回车换行符（下一行行首） 10
\r 回车符（本行行首） 13
\t 制表符 9
\v 竖向跳格 11
\b 退格（删除） 8
\f 走纸换页 12
\a 鸣铃 7
\\ 反斜杠符’\‘ 92
\‘ 单引号符 39
\“ 双引号符 34
\ddd 1~3位八进制数所代表的字符，d∈[0, 7] 注：1~3位和1~2位意思是不必非得满3位或2位，如\xah也是符合规则的，\xa是一个字符，h是另一个字符。
\xhh
（这里的x指以x开头）		 1~2位十六进制数所代表的字符，h∈[0, f]

二、Tips

  1. 给定一个数，对其某几位求反==^1（与1异或），某几位不变==^0（与0异或）。

    short a，a高8位求反，低8位不变，语句为 a^0xFF00

  2. 计算字符串长度，记得统计最后的\0。

  3. (int)(x+y)，将x+y的值转成int。(int)x+y，将x转成int再加y。

  4. 结构体本质上就是一种人为定义的变量类型，其声明与使用与其他变量别无二致。

    1. typedef struct ss {
    2.  char name[10]
    3. }stu;
    4. stu s[10];  //结构体数组
    5. stu *ps;  //这是一个指向结构体变量的指针

  5. sizeof(参数)不会计算它的参数

  6. 声明数组的时候，有的编译器不会给数组的元素赋初值0，因此如果要用到0判断，请手动赋值！
  7. sizeof会计算字符串声明时的长度，即char a[10]字符串中间有\0，sizeof(a)=10

但strlen会计算字符串的实际长度，也就是到\0为止（\0不算进长度）。

  1. 中的开方函数，直接sqrt()调用即可，前面不需要加math.。
  2. aeb表示ax10b。使用该类型数字不需要引入math.h头文件
  3. prim算法找边，是找已经收纳的点集所引出的所有边里最短的。
  4. .c文件编译后产生.obj，链接后产生.exe。
  5. ""空字符串，问字符串的长度是0，问字符串的大小是1B。

三、指针相关

  1. 将指针作为函数形参，在函数中对其进行重新指向（如开辟一段新的地址让形参指针指向它或是将其指向另一个地址）是无效的。因为此时传入函数的是目标指针的形参，即副本，因此函数结束后形参消失，实参地址依旧没有改变。如果想要改变实参的地址，那么我们就需要把实参的地址传入进去，也就是传入一个二级指针，即地址的地址。


    1. int a[10] = {19, 23, 44, 17, 37, 28, 49, 36}, *p=a;
    2. (p+=3)[3]的值为49

    p+=3后p指向了17，则后接[ ]运算符可以看做，从17开始有一个新的数组b且b[0] = 17，则b[3] = 49

  3. int a, *p=&a;，则*p, p[0], *&a均可以正确取得a的值，但*&p不可以。

四、队列

4.1 队列的链式存储

  1. 链队为空条件：Q.front == NULL且Q.rear == NULL。
  2. 链队中，队首和队尾指针的值相同，表示该队列为一个元素。

  3. 链队中只有一个结点的条件为(front == rear) && (front != NULL)。

    4.2 循环队列

  4. 当利用大小为n的数组存储循环队列时，队列最大长度为n-1 (牺牲一个位置)。


  5. 五、树&二叉树

  6. 树——>二叉树：左孩子右兄弟法

  7. 二叉树——>森林：
    1. 首先，二叉树根结点的右边得有兄弟，否则你怎么开枝散叶变成森林？
    2. 按照左孩子右兄弟，逆向将每个兄弟的子孙后代变成树
  8. 一次/依次？推入结点生成二叉排序树：每个结点都从根结点开始比较，小于往左走，大于往右走，直到找到空节点为止。
  9. n个结点完全二叉树，深度为log2n向下取整+1或log2(n+1)向上取整。
  10. 二叉树是非线性数据结构，可表达为顺序存储结构和链式存储结构都能存储。
  11. 从具有N个结点的二叉搜索树中查找一个元素时，在最坏情况下的时间复杂度为O(n)。
  12. 向二叉搜索树中插入一个元素时，其时间复杂度大概为O(log2n)。
  13. n0 = n2 + 1（度为2的结点比度为0的结点多1个）。

六、哈夫曼编码

  1. 构造哈夫曼树：

    1. 首先，将给出的序列递增排序！！

    2. 每次找权值最小的两个点拼成一个树，使用过的结点做个标记；

      若给一个字符串，每个字母出现的次数就是其权值

    3. 将合并后的根结点按照排序插入序列中，继续从序列中选择最小的两个合并，以此类推；

  2. 哈夫曼编码：

    1. 从哈夫曼树的根结点，往左是1/0，往右是0/1

      每走一步就是一个二进制编码。因此算出每个字母所需的编码*出现的次数，加起来就是解码的二进制位数

  3. 编码的总长度=字符对应哈夫曼编码的长度*出现的概率，再相加

  4. 带权路径长度WPL = 结点的权 x 从跟到结点的路径长度，再相加

    七、关键路径

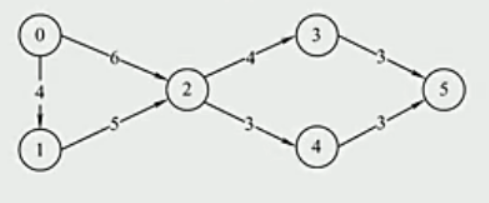
    image.png
    （1）
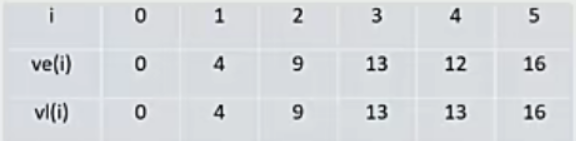
    image.png
    （2）
    image.png
    （3）
    image.png

  5. 找点 i 的最早 ve(i)、最晚时间 vl(i)

最早：把走到这个点的所有路径的权值相加，取最大的值 来的时候取最大值
最晚：最早填完了以后，把最后一个点的最早时间抄下来作为它的最晚时间，然后倒过去依次减边的权值，取最小的值 回的时候取最小

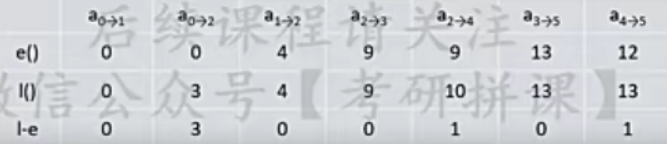
image.png

  1. 找边的最早 e(i)、最晚 l(i)

最早：边的最早就是起点的最早时间
最晚：边的最晚就是终点的最晚时间 减 边的权

  1. 将表2的 l(i) - e(i) 得到 d，d=0的边就是关键路径，这些边的长就是关键路径的长度

八、广义表

  1. 广义表的长度：广义表中数据元素的数量。一个原子算做是一个元素，一个子表也只算做一个元素。

  2. 广义表的深度，指的是广义表中括号的重数。

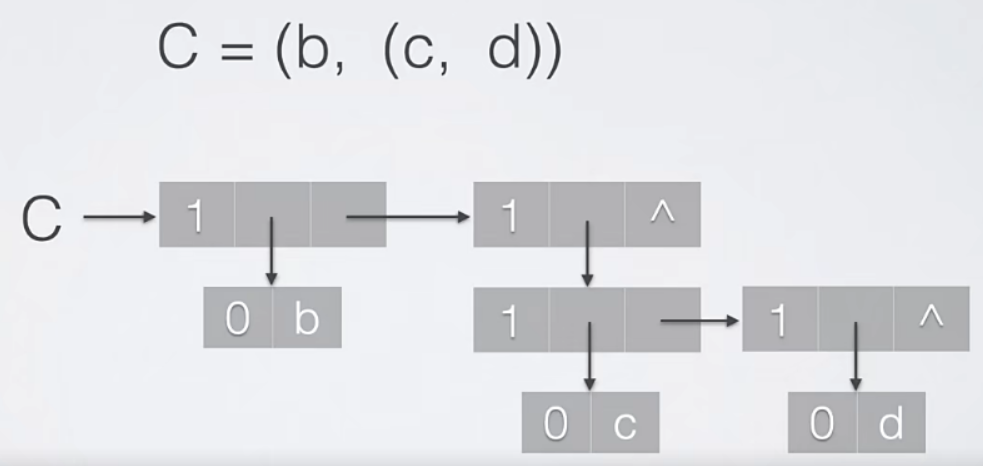
    1. C = ((a,b))  //长度为1,深度为2

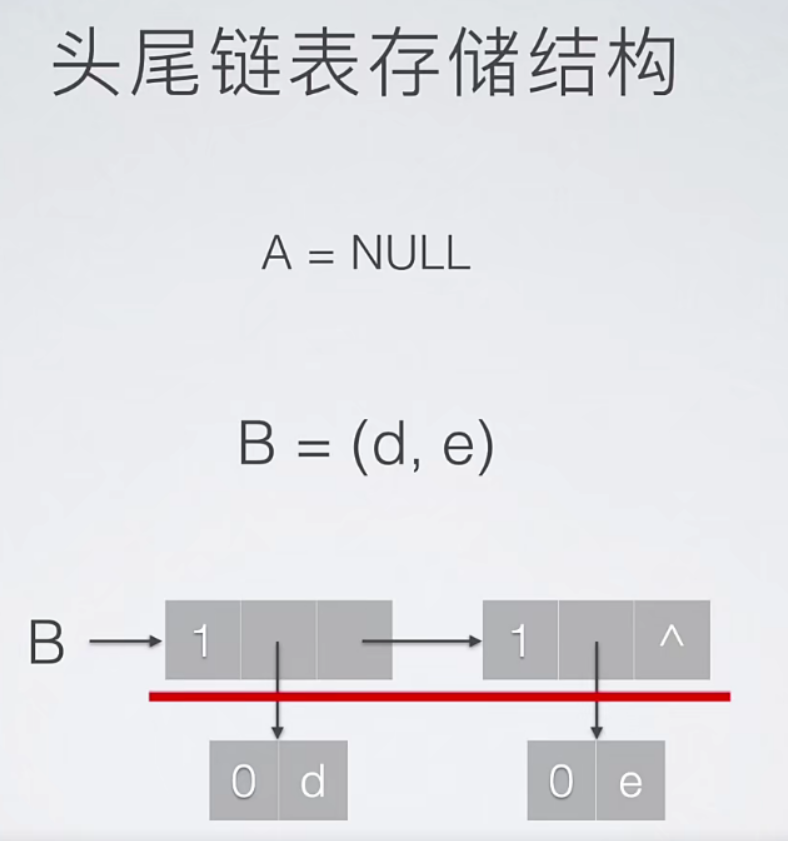
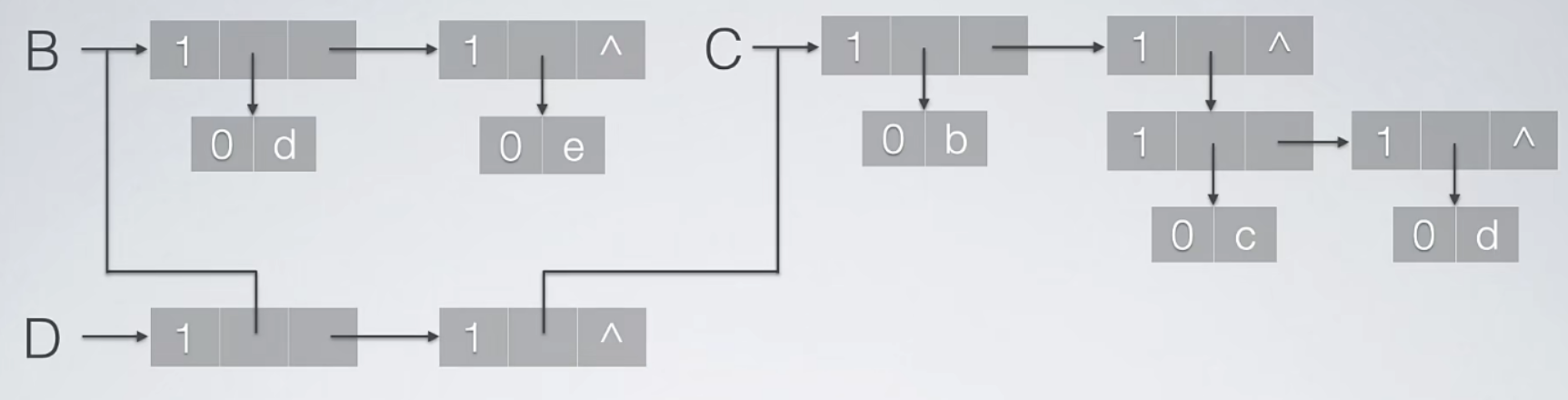
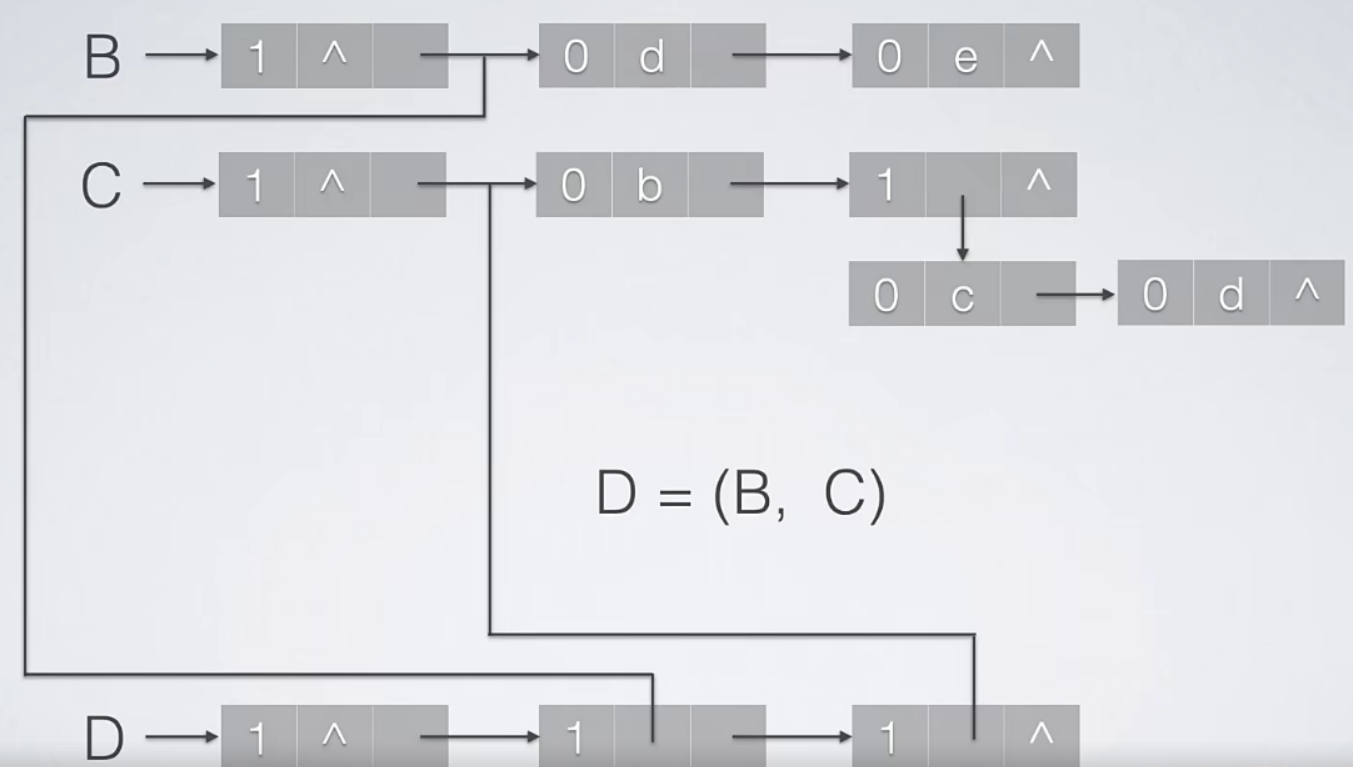
    8.1 头尾链表存储结构

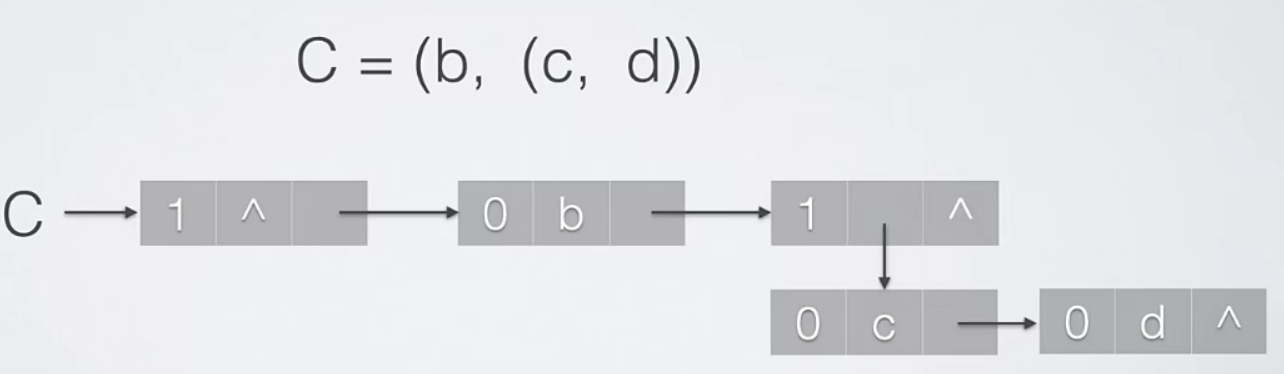
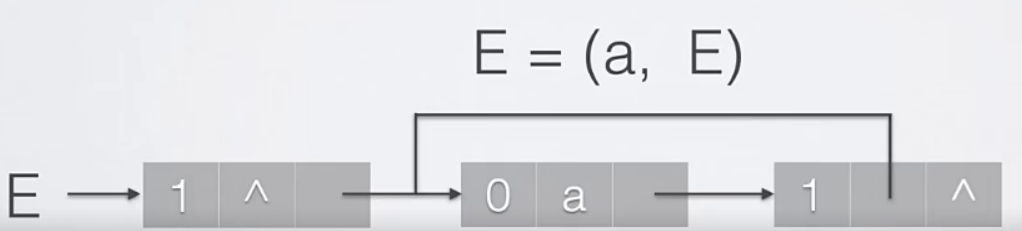
    image.png
    image.png
    D=(B,C)
    image.png

    8.2 扩展线性表存储结构

    image.png
    image.png
    image.png
    image.png
    image.png

    九、查找

    9.1 散列函数

  3. 直接定址法：题目直接给出散列函数H(key)

  4. 除留余数法：设表长为m，H(key)=key%p，p为不大于m但最接近m的质数

    9.2 处理冲突

  5. 采用什么方法处理冲突的，计算查找次数时就按照这个方法来

  6. 拉链法计算查找失败时，一般情况下与空指针的比较不算作1次

    9.3 二叉查找

  7. 向二叉查找中插入一个元素，其时间复杂度大概为O(log2n)

    9.4 折半查找

  8. ASL成功=层数 乘 该层节点数，然后 相加，再 除 总节点数

ASL失败=所有缺了左/右孩子(也就是查找失败的地方)的结点数，然后 乘 层数，再相加，最后 除 总的失败地方的个数。注意，失败地方的层数，是按照它的父节点的层数算的，不要算到下一层去了。

  1. 二分查找一个元素，查找长度就是从根结点开始的比较次数，不要去数树的深度！


  2. 十、图

    10.1 图的存储

    邻接矩阵法

  3. 有向、无向图，有边为1，没有边为0

  4. 如果边有权，则有边就填权值，没有就填无穷（表示到不了）
  5. 邻接矩阵为A，则A**n**[i][j] 表示从i到j长度为n的边有几条
  6. 邻接矩阵找深度优先：

与邻接表法类似，从第一行开始走，到1的时候说明有边，然后跳到对应的结点的行；
从新的行按照上面的方法继续走，每当走到一个没出现过的新结点记录，以此类推走到底；
如果发现某个结点后面的都出现过了，当做全部走完了，然后往上回退到最近的没有走完的一层继续走；

  1. 邻接矩阵找深度优先：

从第一行开始，把所有1都走一遍，记录下来；
把这个记录当做一个新的表，从第一个点开始，按照之前的方法，走完了就找后面一个点走；
直到所有的点都被遍历到。

邻接表法

  1. n个结点竖着写n行两列，左边填结点，右边空着表示指针域；

每个结点连着谁就顺次往后面挂，写完了就在最后一个点的指针域填^表示结束；
无向图1 to 2和2 to 1都要写，每个点后面挂着的点无所谓前后顺序；
有向图按照箭头顺序写就行了。

  1. 邻接表找深度优先：

从头开始往后走，每走一个做个标记；
每出现一个前面没有的新结点，就进到新节点里走，以此类推；
如果发现某个结点后面的都被走过了，全部标记，然后往上回退到最近的没有走完的一层继续走；
以此类推直到所有的结点都被标记。

  1. 用邻接表表示图进行深度优先遍历（DFS）时，通常实现其算法采用的结构是栈。

广度（BFS）采用的是队列。

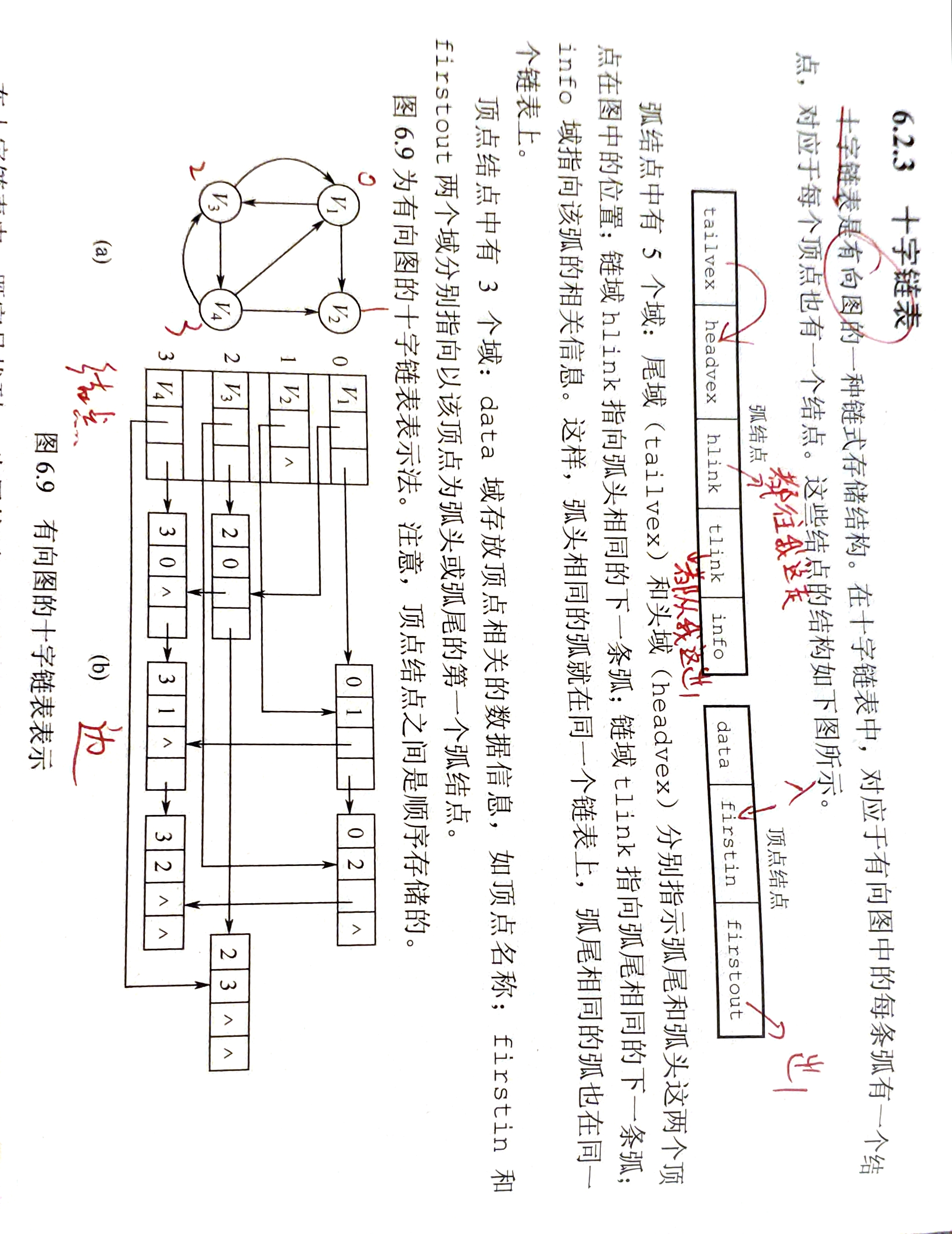
十字链表法（有向图）

image.png

邻接多重表（无向图）

10.2 无向图

  1. 为了保证一个有n个顶点的无向图是连通的，这个图至少要有 (n-1)*(n-2)/2+1 条边。
  2. 有n(n-1)/2条边的无向图称为完全图（也就是边数最多）。
  3. 所有顶点度数和 = 2 x 边数 【一条边连接两个点，就是2个度】。
  4. n个顶点的无向图的邻接表中，结点总数最多有n(n-1)个。

10.3 有向图

  1. 有n(n-1)条边的无向图称为有向完全图。

10.4 连通图

  1. 含有n个顶点的连通图中的任意一条简单路径，其长度不可能超过n-1。
  2. 一个具有n个顶点的连通图生成的最小生成树中，具有n-1条边。

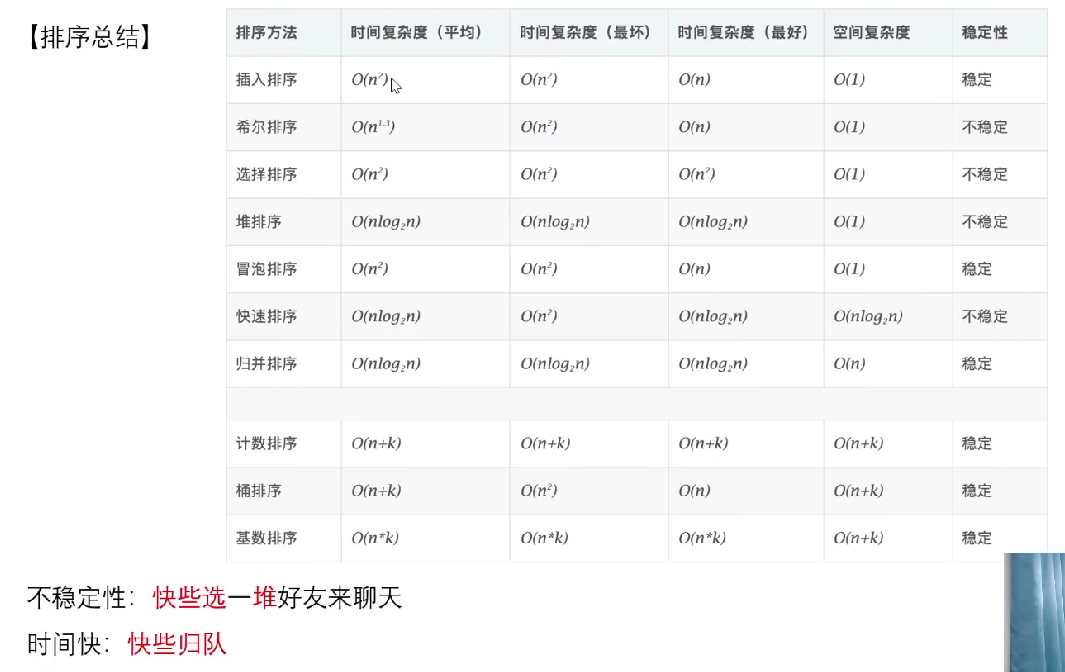
十一、排序

image.png

快速

  1. 两个指针，low指头，high指尾。

以第一个元素为轴（将它暂存到别处，视作删除），high--从右边找比它小的，找到了就放到low;
接着low++从左边找比它大的，找到了就放到high;
当low和high相等时，将刚刚暂存的轴心元素放到low，中间没有改变的元素照抄下来。
至此，一趟排序完毕。

  1. n个元素快速排序，最差的时间复杂度为O(n2)。

拓扑

  1. 每次找入度为0的结点，然后将它和从它射出的所有边删除，以此类推

    堆

  2. 向堆中插入一个元素，其时间复杂度为O(log2n)

  3. 向堆插入：

插入元素先放到堆底（数组最后），然后按照大/小根堆调整
从堆删除：
将要删除的元素和堆底元素交换，然后把要删的删除，接着按照大/小根堆调整

  1. 堆的形状是一颗完全二叉树。
  2. 堆排序：

将初始堆（给出的一组数据）按照满二叉树逐行放进去；
按要求调整为大/小根堆（升序/降序排列）；
将堆顶和堆底元素互换，也就是此时数据中最大的和最后一个交换（从这一步开始才算做一次排序）；
堆顶元素换下去后用虚线连接，此后不对它进行处理；
堆底元素换上去后，重新按照大/小根堆调整；
以此类推，直到排序完成。

归并

  1. n个元素归并排序，每一趟归并的时间复杂度为O(n)。