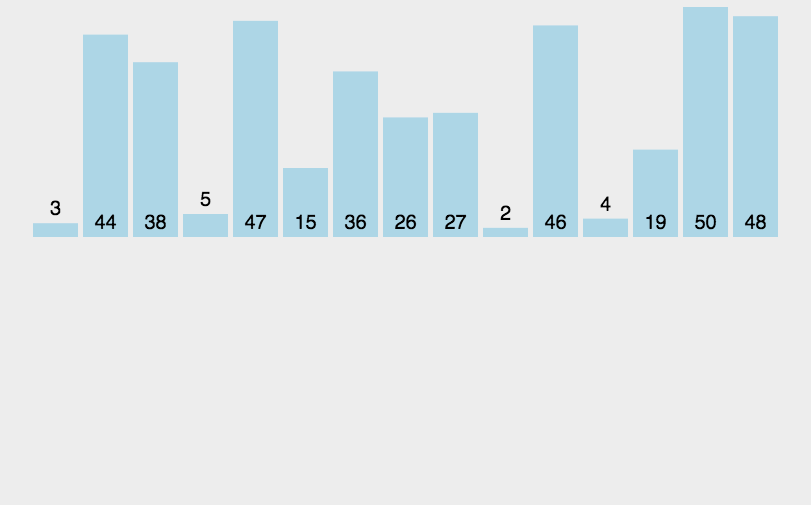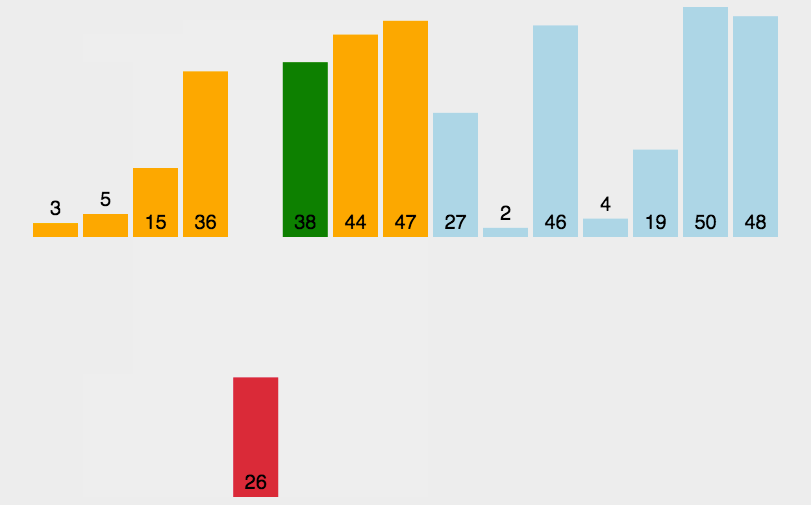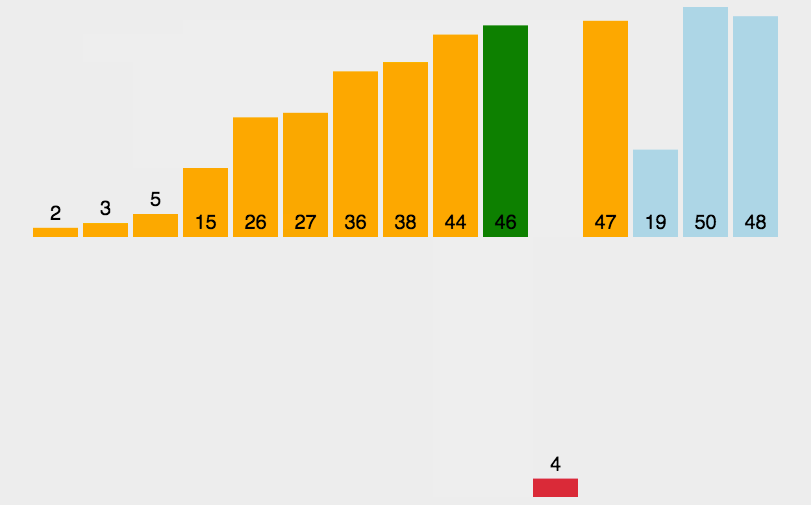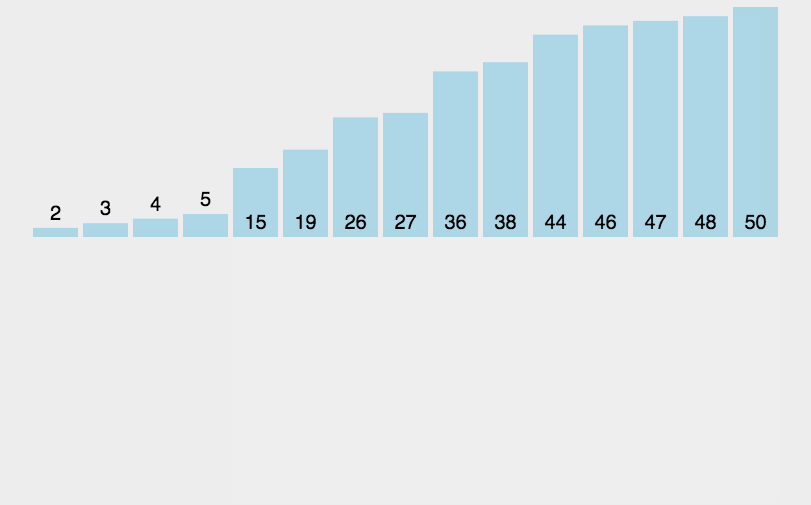
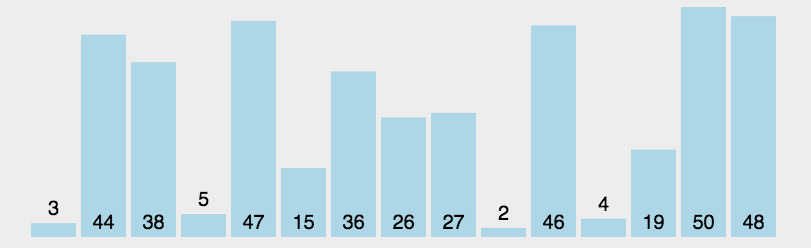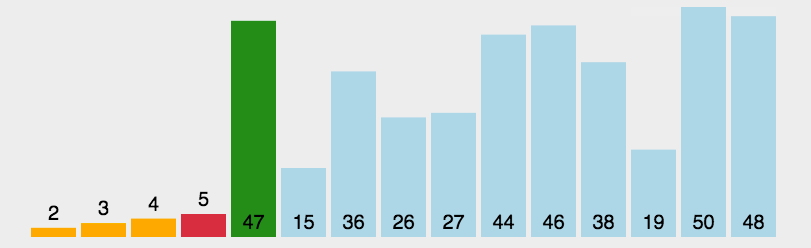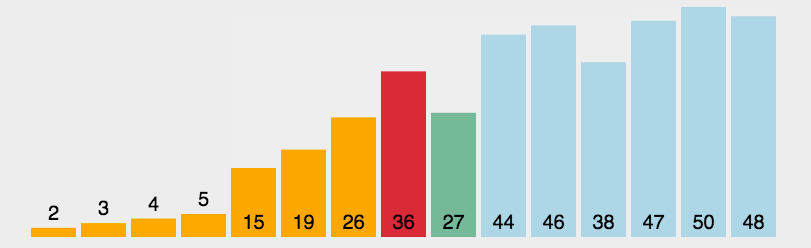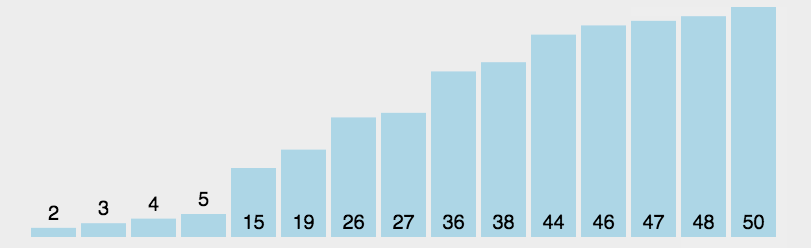
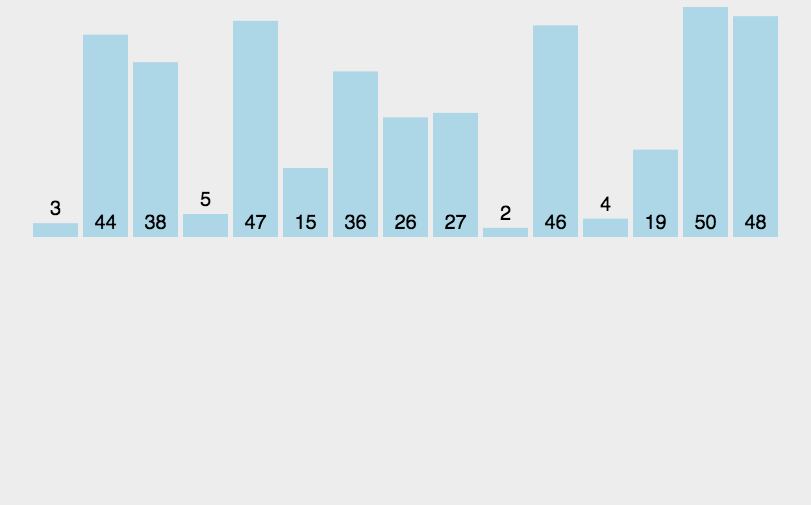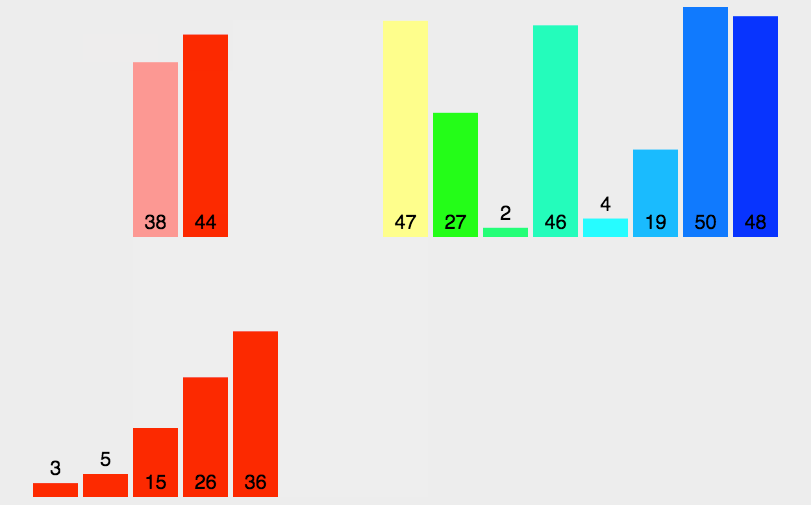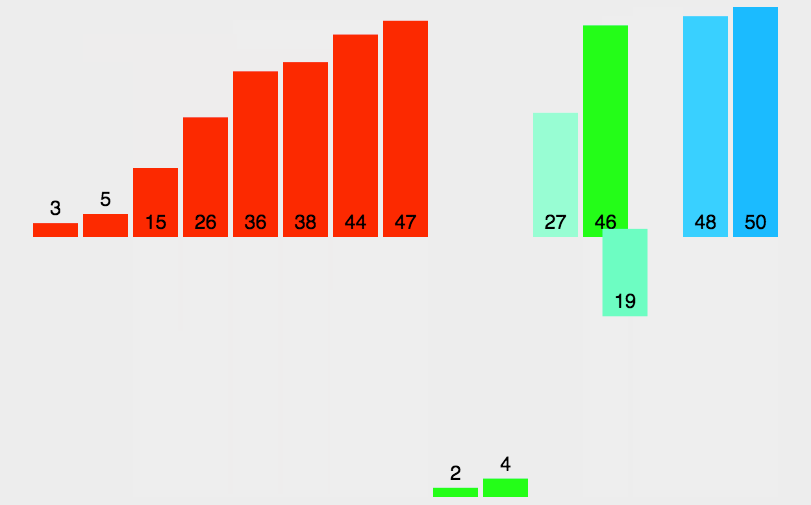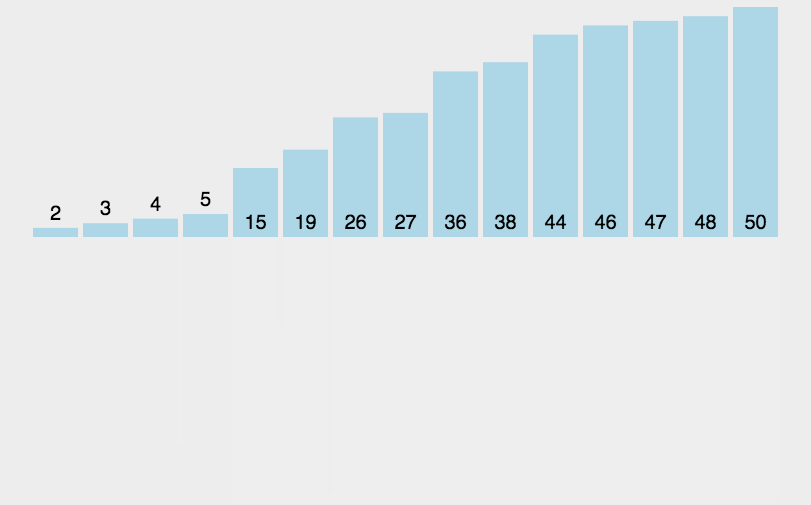
排序效率：
我认为单次遍历结果越有序，效率越高
Arrays.sort()——>底层默认是快速排序——>但是极容易造成栈溢出
排序舞蹈（别点） 排序算法 - 图1

1 插入排序

插入排序.gif

原理

打扑克，抓牌，每次遇到更小的就插到前边

性能

时间复杂度
最好情况——>本身有序——>O(n)——>越有序越快
最坏情况——>本身逆序——>O(n^2)
空间复杂度
O(1)
稳定性
——>if (arr[j] > tmp) {稳定
——>if (arr[j] >= tmp) {不稳定

  1.     public static void insertionSort(int[] arr) {
  2.         for (int i = 0; i < arr.length; i++) {
  3.             int tmp = arr[i];
  4.             int j = i - 1;
  5.             for (; j >= 0; j--) {
  6.                 if (arr[j] > tmp) {
  7.                     arr[j + 1] = arr[j];
  8.                 } else {
  9.                     //可以省略arr[j+1] = tmp;
  10.                     break;
  11.                 }
  12.             }
  13.             arr[j + 1] = tmp;
  14.         }
  15.     }

2 希尔排序

原理

优化的插入排序，主体部分分组，gap/3+1个组，i从gap开始，外层i++，内层j从i-gap开始（第一次i=gap也就是第一次j=0），每次减gap，直到最后gap = 1也就是一次正式的插入排序

性能

时间复杂度：
O(n1.5)——>最坏情况O(n^2)
空间复杂度：
O(1)
稳定性：
因其跳着分组不能保证相同数据的原有顺序，所以不稳定

  1. public static void shellSort(int[] array) {
  2.         int gap = array.length;
  3.         while (gap > 1) {
  4.             shell(array, gap);
  5.             gap = (gap / 3) + 1;//或者 gap/2
  6.         }
  7.         shell(array, 1);
  8. /*
  10.         //分组次数（length）以及个数（元素）
  12.         int[] drr = {5, 3, 1};
  13.         //依次分组——>遍历drr
  14.         for (int value : drr) {
  15.             shell(array, value);
  16.         }
  17. */
  18.     }
  20.     private static void shell(int[] array, int gap) {
  21.         int i = gap;
  22.         //i++每组都进行插入排序，i+=gap则是按组进行，可能不能完全遍历
  23.         for (; i < array.length; i++) {
  24.             int tmp = array[i];
  25.             int j = i - gap;
  26.             for (; j >= 0; j = j - gap) {
  27.                 if (array[j] > tmp) {
  28.                     array[j + gap] = array[j];
  29.                 } else {
  30.                     //可以省略arr[j+1] = tmp;
  31.                     break;
  32.                 }
  33.             }
  34.             array[j + gap] = tmp;
  35.         }
  36.     }

3 选择排序

选择排序.jpg

原理

外层i内层j，每次遇见前大于后的也就是arr[i]>arr[j]的就互换

性能

时间复杂度：
O(n^2)（好坏都是）
空间复杂度：
O(1)
稳定性：
稳定

  1. static void selectSort(int[] array) {
  2.         for (int i = 0; i < array.length-1 ; i++) {
  3.             for (int j = i + 1; j < array.length; j++) {
  4.                 if (array[j] < array[i]) {
  5.                     int tmp = array[i];
  6.                     array[i] = array[j];
  7.                     array[j] = tmp;
  8.                 }
  9.             }
  10.         }

4 堆排序

堆排序.gif
从小到大排序——大堆
从大到小排序——小堆
每一次排序，确定一个当前最大的数，useSize--;

_

原理

使用end = array.length-1最后的结点与0下标交换
调用adjust方法调整使其再次成为大根堆
轮转至end = 0意味着每个位置都放到堆顶调整过，保证其数组整体顺序

adjust调整

传入树，parent结点，以及长度len
利用双亲结点得到其子节点下标
在确认其子节点存在后，进行调整
子节点val大于双亲结点val，则交换，同时交换下标
否则，跳出循环
_

createHeap创建大根堆

将二叉树的每个双亲结点放入调整函数
创建出来的尽管是大根堆，但是并不能够保证其左右同高度结点之间的顺序是否正确

heapSort堆排序主体

创建大根堆
end遍历调整堆
得到顺序数组

性能

时间复杂度 O(n*logn)
空间复杂度O(1)
稳定性

方法：_

  • adjust——>调整
  • createHeap——>创建堆

  • heapSort——>堆排序主体 ```java public static void adjust(int[] array, int parent, int len) {

    1.   int child = parent*2+1;
    2.   while (child < len) {
    3.       if(child+1 < len ) {
    4.           child++;
    5.       }
    6.       if(array[child] > array[parent]) {
    7.           int tmp = array[child];
    8.           array[child] = array[parent];
    9.           array[parent] = tmp;
    11.           parent = child;
    12.           child = 2*parent+1;
    13.       }else{
    14.           break;
    15.       }
    16.   }

    }

    public static void createHeap(int[] array){

    1.   for (int i = (array.length-1-1)/2; i >= 0; i--) {
    2.       //i为每棵树的parent结点
    3.       adjust(array,i,array.length);
    4.   }

    }

    public static void heapSort(int[] array) {

    1.   //大堆——>O(n)
    2.   createHeap(array);
    3.   //排序——>O(n*logn)
    4.   int end = array.length-1;//最后一位，用于交换
    5.   while(end > 0) {
    6.       //当前节点与0位置交换位置
    7.       int tmp = array[0];
    8.       array[0] = array[end];
    9.       array[end] = tmp;
    10.       //换完调整
    11.       adjust(array,0,end);
    12.       end--;
    13.   }

    }

  2. <a name="8pC3k"></a>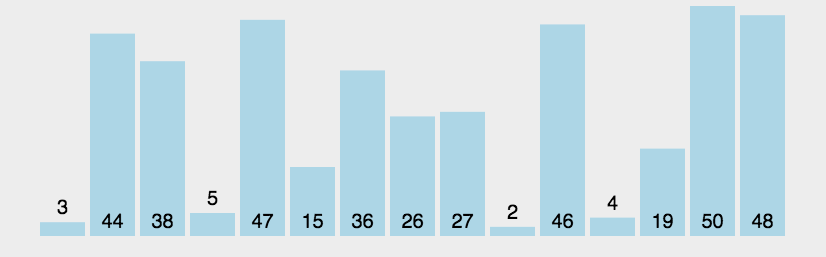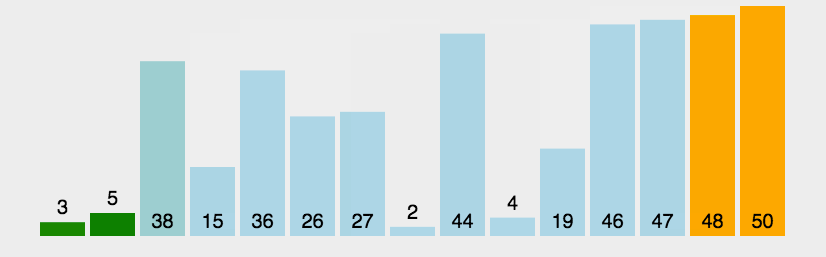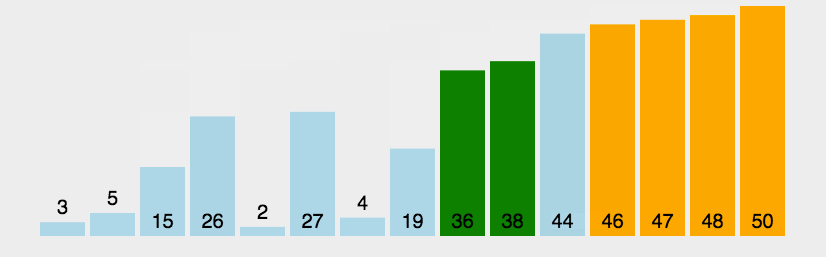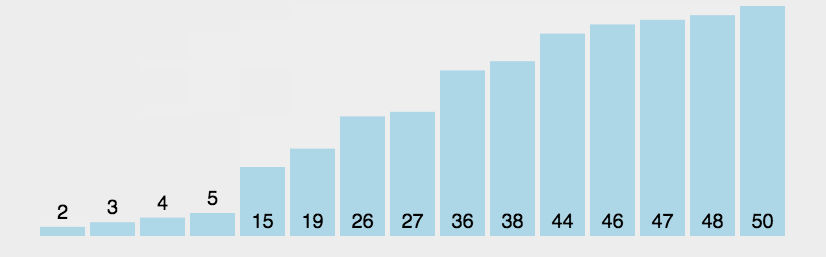
  3. ## 5 冒泡排序
  4. ![冒泡排序.jpg](https://cdn.nlark.com/yuque/0/2021/jpeg/700185/1620897789520-db810693-d95b-4662-8b2e-bc376bf407fb.jpeg#align=left&display=inline&height=257&margin=%5Bobject%20Object%5D&name=%E5%86%92%E6%B3%A1%E6%8E%92%E5%BA%8F.jpg&originHeight=257&originWidth=826&size=466890&status=done&style=none&width=826)
  5. <a name="HfjRj"></a>
  6. #### 原理
  7. 外层i内层j，i是趟数，j是具体每趟操作，内层循环中，每挨着的两个前大于后，对调
  8. <a name="FuYAw"></a>
  9. #### 优化
  10. 外层加一个flg默认false，如果进了内部的if则置true，外层循环最后加一个if判断，为假，则意味着没进入已经正序了，直接跳出
  12. 时间复杂度：<br />O(n^2)（未优化则好坏都是）<br />               优化后，最好情况O(n)，最坏情况O(n^2)<br />空间复杂度：<br />O(1)<br />稳定性：<br />if (array[j] > array[j + 1]) {稳定<br />              if (array[j] >= array[j + 1]) {不稳定
  14. ```java
  15. public static void bubbleSort(int[] array) {
  16.         //趟数
  17.         for (int i = 0; i < array.length; i++) {
  18.             //每趟,-1意味着最后一位没必要和自己比，-i意味着后i个数据已经是有序的了
  19.             boolean flg = false;
  20.             for (int j = 0; j < array.length - 1 - i; j++) {
  21.                 if (array[j] > array[j + 1]) {
  22.                     //交换
  23.                     int tmp = array[j];
  24.                     array[j] = array[j + 1];
  25.                     array[j + 1] = tmp;
  26.                     flg = true;
  27.                 }
  28.             }
  29.             //优化，如果某一次没有发生交换，则flg没有置true
  30.             if(!flg)    break;
  31.         }
  33.     }

6 快速排序

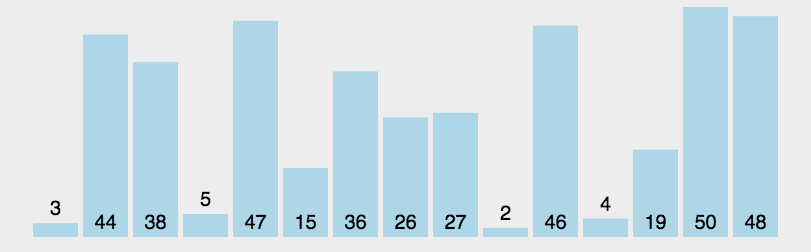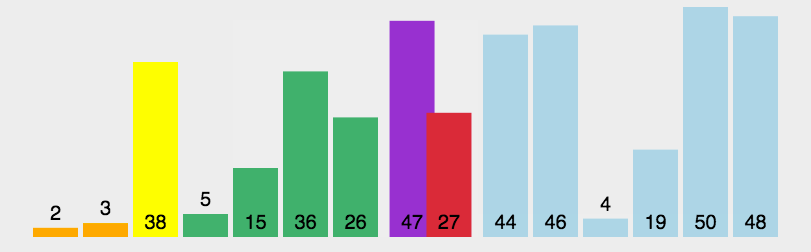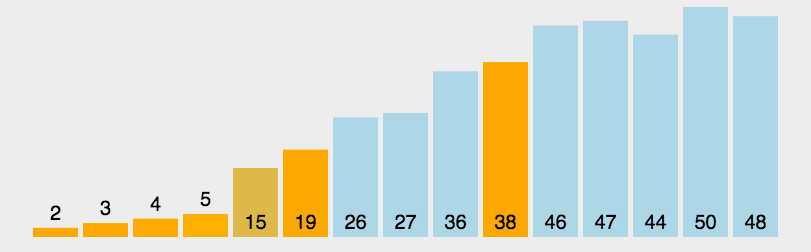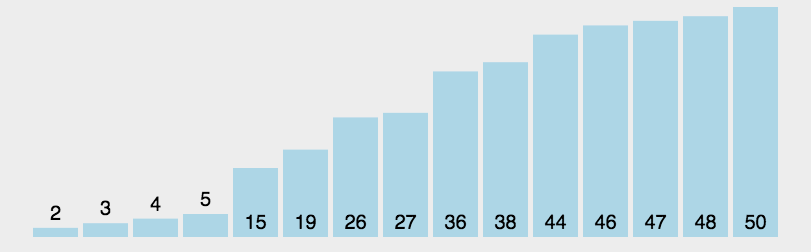
快速排序.gif

  1. public static int partation(int[] array, int start, int end) {
  2.         int tmp = array[start];
  3.         while (start < end) {
  4.             while(start < end && tmp <= array[end]){
  6.                 end--;
  8.             }
  9.             if(start >= end){
  10.                 array[start] = tmp;
  11.                 break;
  12.             }else{
  13.                 array[start] = array[end];
  14.             }
  16.             while(start < end && array[start] <= tmp){
  17.                 start++;
  18.             }
  19.             if(start >= end){
  20.                 array[start] = tmp;
  21.                 break;
  22.             }else{
  23.                 array[start] = array[end];
  24.             }
  26.         }
  27.         return start;
  28.     }
  30.     public static void quick(int[] array, int low, int high) {
  31.         //终止条件
  32.         if (low >= high) return;
  33.         int par = partation(array, low, high);
  34.         //par左
  35.         quick(array, low, par - 1);
  36.         //par右
  37.         quick(array, par + 1, high);
  39.     }
  41.     public static void quickSort(int[] array) {
  42.         quick(array,0,array.length-1);
  43.     }

原理

  1. 在待排序区间选择一个基准值
    1. 选择左边或者右边
    2. 随机选取
    3. 几数取中法
    2. 做 partition，使得小的数在左，大的数在右
    1. hoare
    2. 挖坑
    3. 前后遍历
    4. 将基准值相等的也选择出来（了解）
    3. 分治处理左右两个小区间，直到小区间数目小于一个阈值，使用插入排序

优化

1）选择边上（左或者右）
2）random随机一个基准
3）三数取中，头、中、尾，找中间的数字作为基准
4）相差不到100时，直接插入排序

  1.     //优化3的方法
  2.     public static void medianOfThree(int[] array, int start,int mid, int end){
  3.         if(array[start] < array[mid]){
  4.             int tmp = array[start];
  5.             array[start] = array[mid];
  6.             array[mid] = tmp;
  7.         }//array[mid] <= array[start]
  8.         if(array[start] > array[end]){
  9.             int tmp = array[start];
  10.             array[start] = array[end];
  11.             array[end] = tmp;
  12.         }//array[start] <= array[end]
  13.         if(array[mid] > array[end]){
  14.             int tmp = array[mid];
  15.             array[mid] = array[end];
  16.             array[end] = tmp;
  17.         }
  18.     }    
  19.     //优化4的insert插入排序
  20.     public static void insertSort(int[] array,int start,int end){
  21.         for (int i = 0; i < array.length; i++) {
  22.             int tmp = array[i];
  23.             int j = i-1;
  24.             for (; j >= start ; j--) {
  25.                 if(array[j] > tmp){
  26.                     array[j+1] = array[j];
  27.                 }else{
  28.                     break;
  29.                 }
  30.             array[j+1] = tmp;
  31.             }
  32.         }
  33.     }        
  34.         //优化4，中间差了不到100个了就用插入排序
  35.         if(high-low+1 < 100){
  36.             insertSort(array,low,high);
  37.             return;
  38.         }
  40.         //优化3，三数取中
  41.         int mid = (low+high)>>>1;//中间相加除以2
  42.         medianOfThree(array,low,mid,high);

优化总结

  1. 选择基准值很重要，通常使用几数取中法
    2. partition 过程中把和基准值相等的数也选择出来
    3. 待排序区间小于一个阈值时（例如 48），使用直接插入排序快排总结

可能出的题目

下列选项可能是快速排序第一趟排序结果的是：

7 归并排序

归并排序.gif

原理

大问题化小，分而治之——>是不是就是递归的思想原则
1.分解2.重排序3.合并
分组原则
每次长度除以二，直到只剩下自己一组

性能

时间复杂度
O(nlogn)
空间复杂度
O(n) 每次递归都申请了数组
稳定性
if (array[s1] <= array[s2]) {// 有=稳定，没=不稳定

  1. public class MergeSort {
  2.     //递归体，用于前半程的拆分
  3.     public static void mergeSortRec(int[] array, int low, int high) {
  4.         //递归终止条件
  5.         if (low >= high) return;
  6.         int mid = (high + low) >>> 1;
  8.         mergeSortRec(array, low, mid);//左
  9.         mergeSortRec(array, mid + 1, high);//右
  11.         merge(array, low, mid, high);
  12.     }
  14.     //合并函数，用户后半程的合并
  15.     public static void merge(int[] array, int low, int mid, int high) {
  17.         //临时数组用于存放合并的数组
  18.         int[] tmp = new int[high - low + 1];
  19.         int k = 0;//数组下标
  20.         //合并两个有序数组
  21.         int s1 = low;
  22.         int e1 = mid;
  23.         int s2 = mid + 1;
  24.         int e2 = high;
  25.         while (s1 <= e1 && s2 <= e2) {
  26.             if (array[s1] <= array[s2]) {//可不可以取等于  有=稳定，没=不稳定
  27.                 tmp[k++] = array[s1++];
  28.             } else {
  29.                 tmp[k++] = array[s2++];
  30.             }
  31.         }
  32.         //谁剩下了谁继续
  33.         while (s1 <= e1) {
  34.             tmp[k++] = array[s1++];
  35.         }
  36.         while (s2 <= e2) {
  37.             tmp[k++] = array[s2++];
  38.         }
  39.         //合并完成
  41.         for (int i = 0; i < tmp.length; i++) {
  42.             array[i + low] = tmp[i];//+low原因：按位拷贝
  43.         }
  44.     }
  46.     public static void mergeSort(int[] array) {
  47.         mergeSortRec(array, 0, array.length - 1);
  48.     }
  49. }

8 排序总结

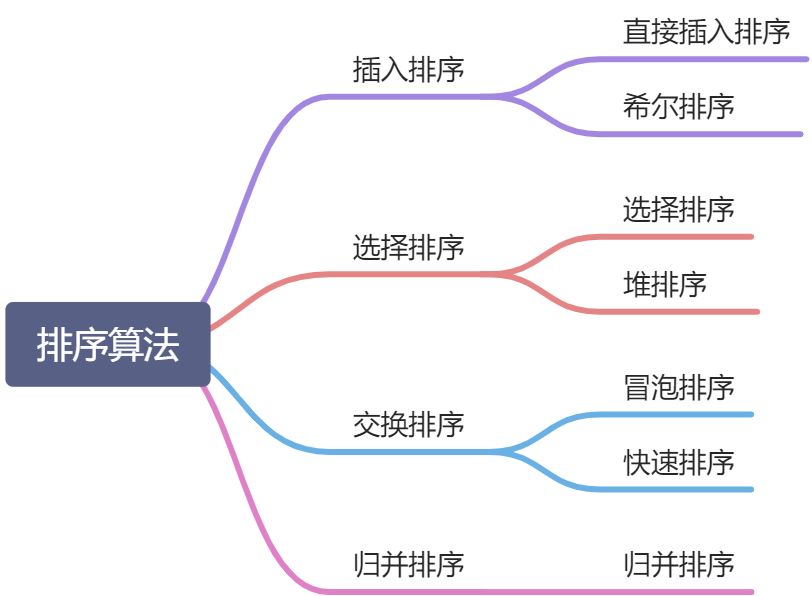
排序分类

海量数据排序

内部排序：将数据全部都存储在了内存上 内存条8G

外部排序：将数据全部在外存上排序的 磁盘
如若现有40G文件，将其切割成我内存放得下大小的若干块，挨个读取排序，再按层归并
（或是说无论给定多大的一个数据，一语归并解决问题）
1.切割文件，使得每个文件当中的数据很小
2.读取文件里面的数据
3.排序
4.合并

按方式分类

比较排序
非比较排序

排序方法 最好 平均 最坏 空间复杂度 稳定性
冒泡排序 O(n) O(n) O(n) O(1) 稳定
插入排序 O(n) O(n) O(n) O(1) 稳定
选择排序 O(n) O(n) O(n) O(1) 不稳定
希尔排序 O(n) O(n) O(n) O(1) 不稳定
堆排序 O(n*log2n) O(n*log2n) O(n*log2n) O(1) 不稳定
快速排序 O(n*log2n) O(n*log2n) O(n) O(log2n) - O(n) 不稳定
归并排序 O(n*log2n) O(n*log2n) O(n*log2n) O(n) 稳定

9 其他非基于比较的排序

计数排序

计数排序.webp

基数排序

List<Queue<Integer>> a = new ArrayList<>();数组每个元素是一个队列
或者链表
十个桶，0.1.2.3.4…8.9
按位比较，个十百千，按当前位上数字大小顺序入桶
基数排序.webp

桶排序