试卷、实验题目 - 算法分析与设计 - 《CS 资料》

题型分配
第一章算法引论
第二章递归算法与分治算法
第三章贪心算法
- 背包问题
- 单源点最短路径
第四章动态规划算法
- 资源分配
实验
参考书籍

题型分配

共六大题
一、填空十小题 10分（第一章）
二、单选五小题 10分
三、判断五小题 10分
四、公式推导一题 10分（生成函数）
五、解答题四小题 45分（背包，单源点，排序，资源分配）
六、算法填空一题 15分（排序）

第一章算法引论

算法的重要特性：确定性，能行性，输入，输出，有限性
算法的基本内容：设计算法，表示算法，确认算法，分析算法，测试程序

1. 什么是算法、频率计数、多项式时间算法、指数时间算法？
算法：能够对一定规范的输入，在有限时间内获得所要求的输出。

若存在一个常数C，使得对于所有n>=0，都有|f(n)| <= C*|g(n)|，则称函数f(n)是O(g(n))。时间复杂度是O(p(n))的算法称为多项式时间算法，这里p(n)是关于n的多项式。不能够这样限制时间复杂度的算法被称为指数时间算法。

2. 什么是算法分析的目的？
分析算法的效益，以求改进。

3. 什么是事前分析和事后分析？
事前分析：求出该算法的一个时间限界函数
事后测试：收集该算法的执行时间和占用空间的统计资料

4. 评价一个算法应从那几个方面考虑？
正确性、易读性、健壮性、时空效率（运行）。

时间复杂度排行：O(1)<O(logn)<O(n)<O(nlogn)<O(n)<O(n)

第二章递归算法与分治算法

生成函数

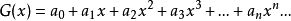
算法分析与设计 - 图1

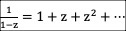
算法分析与设计 - 图2

算法分析与设计 - 图3

生成函数求解递归

课后习题 P59 第 5 题

算法分析与设计 - 图4

递归算法

课后习题 P59 第 6 题：有 n 级台阶，一个人每次上一级或者两级，问有多少种走完 n 级台阶的方法？分析该递归算法的时间复杂度。

int calcStep(int n)
{
    if (n == 1)
    {
        return 1;
    }
    else if (n == 2)
    {
        return 2;
    }
    int count[n + 1];
    count[1] = 1;
    count[2] = 2;
    for (int i = 3; i < n + 1; i++)
    {
        count[i] = count[i - 1] + count[i - 2];
    }
    return count[n];
}
void main()
{
    int n = 20; //总共还要上20层
    int allCount = calcStep(n);
    print("要上20层，总共有：%d" + allCount);
}

分治算法

课后习题 P59 第 11 题：试用分治算法求在含有 n 个元素的数组中的最大最小元素？

#include "stdio.h"
#include "stdlib.h"
#include "time.h"
#define ARRAY_SIZE 50
void FindMinMax(int *Array, int left, int right, int *min, int *max)
{
    if ((right - left) == 1)

    {
        *max = Array[left];

        *min = Array[right];
        if (Array[left] < Array[right])

        {
            *max = Array[right];
            *min = Array[left];
        }
    }
    else if ((right - left) == 0)

    {
        *max = *min = Array[left];
    }
    else
    {
        int min1, min2, max1, max2;
        FindMinMax(Array, left, (right - left) / 2 + left, &min1, &max1);
        FindMinMax(Array, (right - left) / 2 + 1 + left, right, &min2, &max2);
        (min1 > min2) ? *min = min2 : *min = min1;
        (max1 > max2) ? *max = max1 : *max = max2;
    }
}

int main(void)
{
    int Array[ARRAY_SIZE];

    int min, max, i;
    srand(time(0));
    for (i = 0; i < ARRAY_SIZE; i++)
    {
        Array[i] = rand() % 100;
        if (i % 5 == 0)
            printf("\n");
        printf("%6d", Array[i]);
    }
    FindMinMax(Array, 0, i - 1, &min, &max);
    printf("\nmin = %d \nmax = %d\n", min, max);
    return 0;
}