5.Longest Palindromic Substring-最长回文子串

题目描述：

输入输出Demo：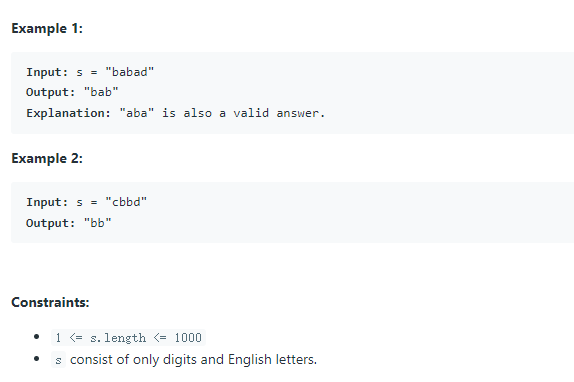

解析：在LeetCode上本题属于Medium难度。用Manacher算法求解。
需要先明白几个概念：1.回文半径数组 2.最右回文右边界 3.取得最右边界时，中心在哪里
回文直径：以一个中心点 i ，往左右扩，其长度为回文直径，例 __i_，那么，扩一半的长度，就为回文半径，例 i_，存入辅助数组(即回文半径数组)
最右回文右边界：例012131210
初始R当前停在-1索引的位置：

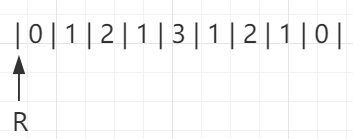
当要扩0的时候，发现没扩的，R停在索引为0的位置：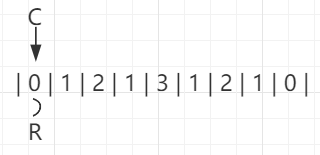

继续扩1，发现没扩的，R停留在索引为1的位置：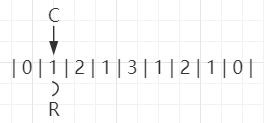

继续扩2，此时R到了索引为3的位置：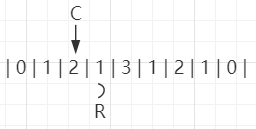

继续扩1，发现没扩的，R保持原来的索引位置：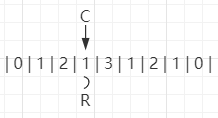

继续扩3，此时R到了末尾：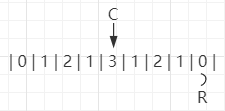

……C继续往右扩，R就是最右回文右边界，C为其中心点

class Solution {
        public String longestPalindrome(String s) {
            //首先预处理，将原字符串转变为例如“#a#b#c#”的形式
            StringBuilder stringBuilder = new StringBuilder("#");
            for (int i = 0; i < s.length(); i++) {
                stringBuilder.append(s.charAt(i)).append("#");
            }
            s = stringBuilder.toString();
            int[] RL = new int[s.length()]; //回文半径数组(保存的是当前字符的回文半径)
            int c = -1, maxRight = -1;  //c为中心点，maxRight为最大回文右边界，初始化为-1
            for (int i = 0; i < s.length(); i++) {  //遍历所有的s，求当前i所指向字符的回文半径
                /**
                 * 有两种可能性
                 *    1.若当前字符在最大回文右边界外面（直接暴力往外扩）
                 *    2.若当前字符在最大回文右边界里面：（此时有3种可能）
                 *       2.1 i'回文在L,R内
                 *       2.2 i'回文在L,R外
                 *      -----> RL[i]=min(RL[i'],R-i)
                 *      2.3 i'回文的左边界与L压线
                 */
                if (i >= maxRight) { //说明i在回文右边界外面(直接暴力往外扩)
                    RL[i] = 1; //i自己算做一个长度，由此向外扩
                } else {  //说明i在回文右边界里面 (2.1和2.2情况)
                    RL[i] = Math.min(RL[2 * c - i], maxRight - i);
                }
                //尝试以i位置往外扩，注意处理边界(全部都往外扩，避免分情况讨论)
                while (i - RL[i] >= 0 && i + RL[i] < s.length()) { // 0<=回文左边界左边一位<=回文右边界右边一位<=s.length()
                    if (s.charAt(i - RL[i]) == s.charAt(i + RL[i])) {  //左边界和右边界的下一个点
                        RL[i] += 1;
                    } else {
                        break;  //没匹配上的直接跳出
                    }
                }
                if (i + RL[i] > maxRight) {
                    maxRight = i + RL[i];  //更新最右边界和中心点
                    c = i;
                }
            }
            int maxLen = 0;
            int centerIndex = 0;
            for (int idx = 0; idx < RL.length; idx++) {
                if (RL[idx] > maxLen) {
                    maxLen = RL[idx];
                    centerIndex = idx;
                }
            }
            return s.substring(centerIndex-maxLen+1,centerIndex+maxLen).replace("#","");
        }
    }