4. Median of Two Sorted Arrays-两个正序数组的中位数

题目描述：

输入输出Demo：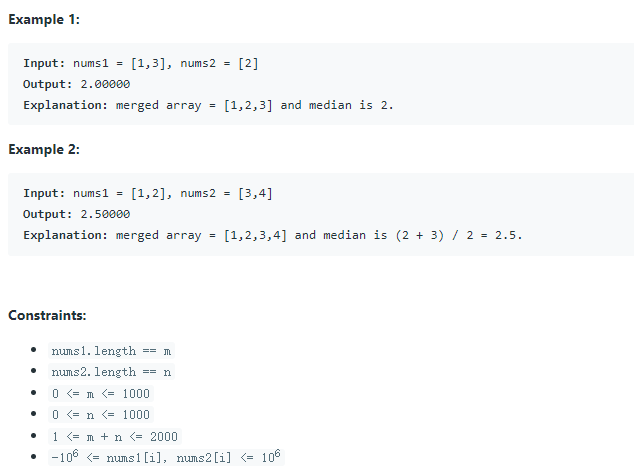

解析：本题在LeetCode上属于Hard难度，面试出现的频率非常高，整体思路是采用划分数组来做。
我们首先理一下中位数的定义是什么，中位数（Median）又称中值，统计学中的专有名词，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合划分为相等的上下两部分。
所以我们只需要将数组进行切分。一个长度为 m 的数组，有 0 到 m 总共 m + 1 个位置可以切。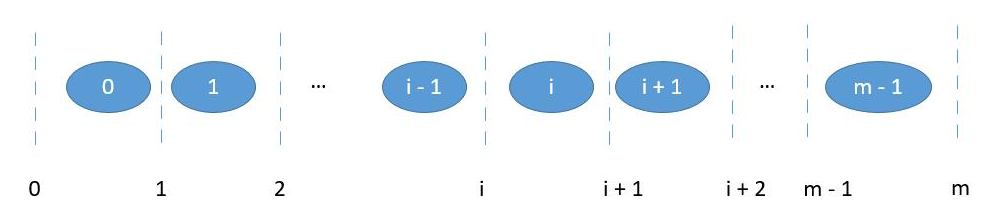

我们把数组 A 和数组 B 分别在 i 和 j 进行切割。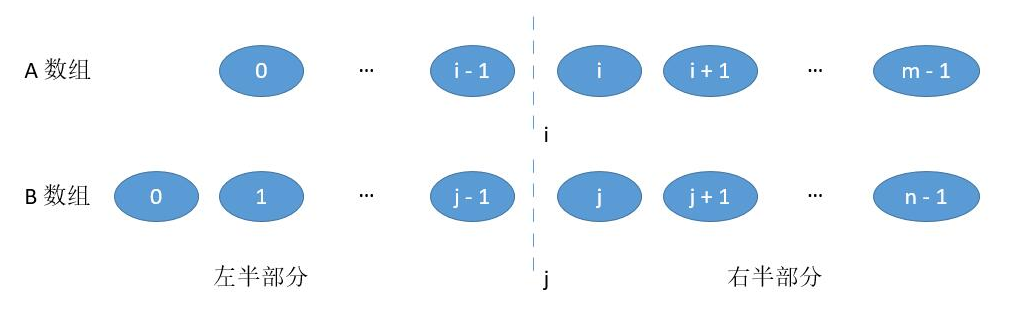

将 i 的左边和 j 的左边组合成「左半部分」，将 i 的右边和 j 的右边组合成「右半部分」。

• 当 A 数组和 B 数组的总长度是偶数时，如果我们能够保证

左半部分的长度等于右半部分
i + j = m - i + n - j , 也就是 j = ( m + n ) / 2 - i
左半部分最大的值小于等于右半部分最小的值
max ( A [ i - 1] , B [ j - 1]）） <= min ( A [ i] , B [ j]））
那么，中位数就可以表示如下 (左半部分最大值 + 右半部分最小值)/ 2。（max ( A [ i - 1 ] , B [ j - 1 ]）+ min ( A [ i ] , B [ j ]）） / 2

• 当 A 数组和 B 数组的总长度是奇数时，如果我们能够保证

左半部分的长度比右半部分大1
i + j = m - i + n - j + 1也就是 j = ( m + n + 1) / 2 - i
左半部分最大的值小于等于右半部分最小的值
max ( A [ i - 1] , B [ j - 1]）） <= min ( A [ i] , B [ j]））
那么，中位数就是 左半部分最大值，也就是左半部比右半部分多出的那一个数。 max ( A [ i - 1 ] , B [ j - 1 ]）
上边的第一个条件我们其实可以合并为 j=(m+n+1)/2−i，因为如果 m+n 是偶数，由于我们取的是 int 值，所以加 1 也不会影响结果。

而对于第二个条件，奇数和偶数的情况是一样的，我们进一步分析。为了保证 max ( A [ i - 1] , B [ j - 1]）） <= min ( A [ i] , B [ j]）），因为 A 数组和 B 数组是有序的，所以 A [ i - 1] <= A [ i]，B [ i - 1] <= B [ i] 这是天然的，所以我们只需要保证 B [ j - 1] < = A [ i] 和 A [ i - 1] <= B [ j] 所以我们分两种情况讨论：
1.B [ j - 1] > A [ i]，并且为了不越界，要保证 j != 0，i != m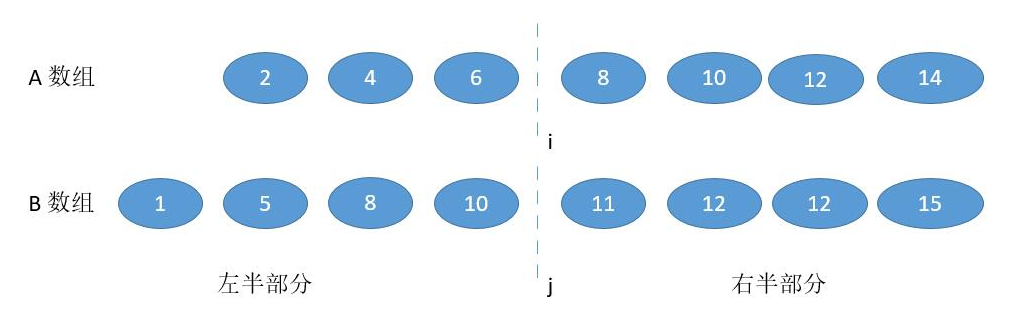

此时很明显，我们需要增加 i ，为了数量的平衡还要减少 j ，幸运的是 j = ( m + n + 1) / 2 - i，i 增大，j 自然会减少。
2.A [ i - 1] > B [ j] ，并且为了不越界，要保证 i != 0，j != n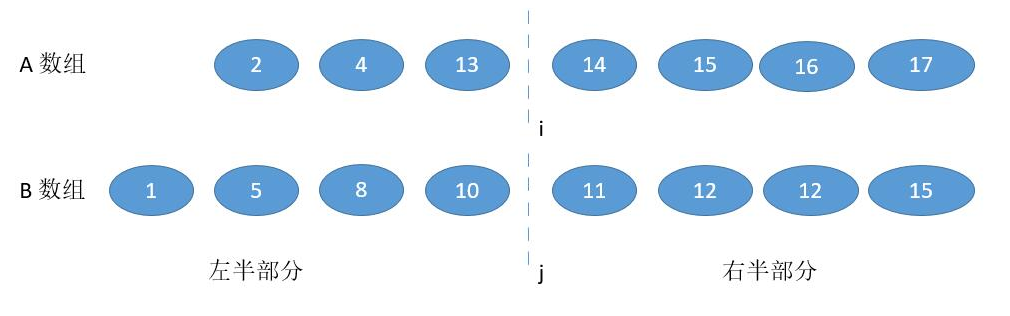

此时和上边的情况相反，我们要减少 i ，增大 j 。
上边两种情况，我们把边界都排除了，需要单独讨论。

3.当 i = 0, 或者 j = 0，也就是切在了最前边。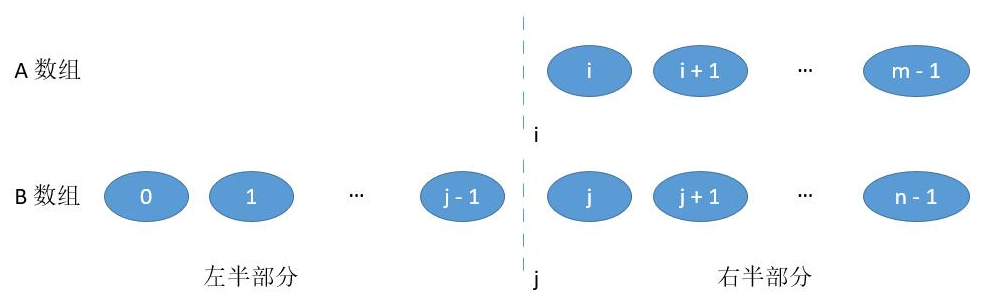

此时左半部分当 j = 0 时，最大的值就是 A [ i - 1] ；当 i = 0 时 最大的值就是 B [ j - 1] 。右半部分最小值和之前一样。
4.当 i = m 或者 j = n，也就是切在了最后边。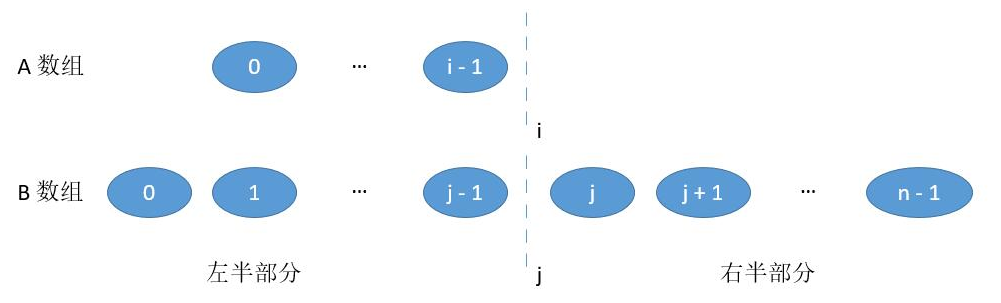

此时左半部分最大值和之前一样。右半部分当 j = n 时，最小值就是 A [ i] ；当 i = m 时，最小值就是B [ j] 。
所有的思路都理清了，最后一个问题，增加 i 的方式。当然用二分了。初始化 i 为中间的值，然后减半找中间的，减半找中间的，减半找中间的直到答案。

class Solution {
        public double findMedianSortedArrays(int[] nums1, int[] nums2) {
            //归并后的大数组一定来自于数组A和数组B的左右两部分
            //把中位数划分到左半部分，满足这样的i,j需2个条件
            //1.i+j=(a_length+b_length+1)/2
            //2.max(A[i-1],B[j-1])<min(A[i],B[i])
            int a_length = nums1.length;
            int b_length = nums2.length;
            //每次都是以长度最小的数组开始
            if (a_length > b_length) {
                return findMedianSortedArrays(nums2, nums1);
            }
//            if (a_length > b_length) {
//                int[] tmp1 = nums1;
//                nums1 = nums2;
//                nums2 = tmp1;
//                int tmp2 = a_length;
//                a_length = b_length;
//                b_length = tmp2;
//            }
            int iMin = 0, iMax = a_length;
            while (iMin <= iMax) {   //保证i的范围
                int i = (iMin + iMax) >> 1;
                int j = ((a_length + b_length + 1) >> 1) - i;  //满足条件1
                if (j != 0 && i != a_length && nums1[i] < nums2[j - 1]) {
                    //说明右半边的数字小了，i的最小范围需要右移
                    iMin = i + 1;
                } else if (i != 0 && j != b_length && nums1[i - 1] > nums2[j]) {
                    //说明左半部分的数大了，i的最大范围需要左移
                    iMax = i - 1;
                } else { //达到要求，并且将边界条件列出来单独考虑
                    int maxLeft = 0;
                    if (i == 0) {
                        maxLeft = nums2[j - 1];
                    } else if (j == 0) {
                        maxLeft = nums1[i - 1];
                    } else { //表明各数组不是左边界
                        maxLeft = Math.max(nums1[i - 1], nums2[j - 1]);
                    }
                    if ((a_length + b_length) % 2 == 1) {  //大数组为基数的话，直接返回中位数
                        return maxLeft;
                    }
                    int minRight = 0;
                    if (i == a_length) {
                        minRight = nums2[j];
                    } else if (j == b_length) {
                        minRight = nums1[i];
                    } else { //表明各数组不是右边界
                        minRight = Math.min(nums1[i], nums2[j]);
                    }
                    return (double) (maxLeft + minRight) / 2;
                }
            }
            return 0.0;
        }
    }