2.8.5 Growth Categories

Orders of growth are designed to simplify the analysis and comparison of computational processes. Many different processes can all have equivalent orders of growth, which indicates that they scale in similar ways. It is an essential skill of a computer scientist to know and recognize common orders of growth and identify processes of the same order.
Constants. Constant terms do not affect the order of growth of a process. So, for instance, and are the same order of growth. This property follows from the definition of theta notation, which allows us to choose arbitrary constants and (such as ) for the upper and lower bounds. For simplicity, constants are always omitted from orders of growth.
Logarithms. The base of a logarithm does not affect the order of growth of a process. For instance, and are the same order of growth. Changing the base of a logarithm is equivalent to multiplying by a constant factor.
Nesting. When an inner computational process is repeated for each step in an outer process, then the order of growth of the entire process is a product of the number of steps in the outer and inner processes.
For example, the function overlap below computes the number of elements in list a that also appear in list b.

>>> def overlap(a, b):
        count = 0
        for item in a:
            if item in b:
                count += 1
        return count
>>> overlap([1, 3, 2, 2, 5, 1], [5, 4, 2])
3

The in operator for lists requires time, where nn is the length of the list b. It is applied times, where is the length of the list a. The item in b expression is the inner process, and the for item in a loop is the outer process. The total order of growth for this function is .
Lower-order terms. As the input to a process grows, the fastest growing part of a computation dominates the total resources used. Theta notation captures this intuition. In a sum, all but the fastest growing term can be dropped without changing the order of growth.
For instance, consider the one_more function that returns how many elements of a list a are one more than some other element of a. That is, in the list [3, 14, 15, 9], the element 15 is one more than 14, so one_more will return 1.

>>> def one_more(a):
        return overlap([x-1 for x in a], a)
>>> one_more([3, 14, 15, 9])
1

There are two parts to this computation: the list comprehension and the call to overlap. For a list a of length nn, list comprehension requires steps, while the call to overlap requires steps. The sum of steps is , but this is not the simplest way of expressing the order of growth.
and are equivalent for any constant because the term will eventually dominate the total for any . The fact that bounds must hold only for greater than some minimum establishes this equivalence. For simplicity, lower-order terms are always omitted from orders of growth, and so we will never see a sum within a theta expression.
Common categories. Given these equivalence properties, a small set of common categories emerge to describe most computational processes. The most common are listed below from slowest to fastest growth, along with descriptions of the growth as the input increases. Examples for each category follow.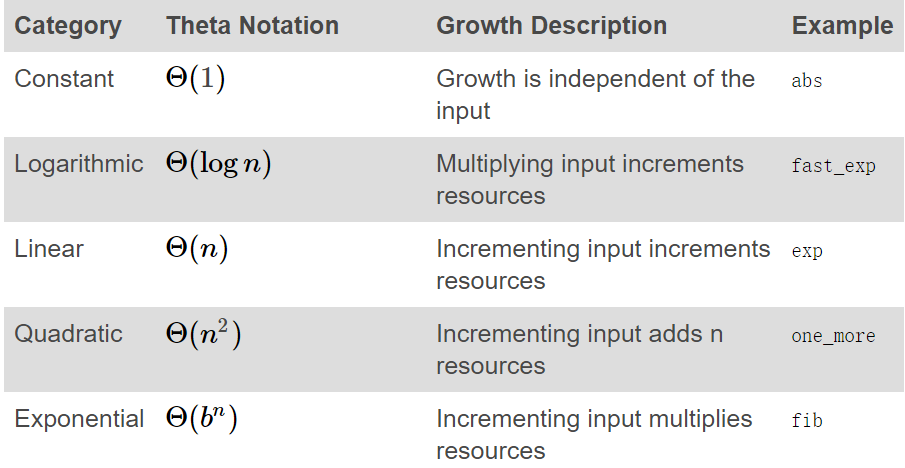

Other categories exist, such as the growth of count_factors. However, these categories are particularly common.
Exponential growth describes many different orders of growth, because changing the base bb does affect the order of growth. For instance, the number of steps in our tree-recursive Fibonacci computation fib grows exponentially in its input nn. In particular, one can show that the nth Fibonacci number is the closest integer to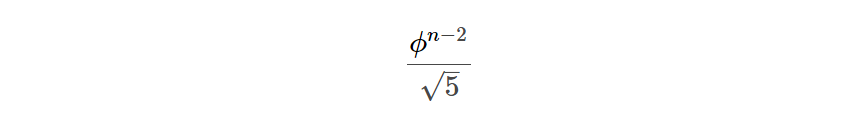

where ϕϕ is the golden ratio: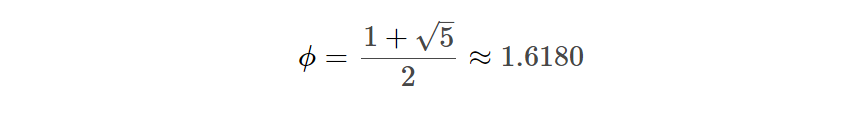

We also stated that the number of steps scales with the resulting value, and so the tree-recursive process requires steps, a function that grows exponentially with .