2.8.2 Memoization

Tree-recursive computational processes can often be made more efficient through memoization, a powerful technique for increasing the efficiency of recursive functions that repeat computation. A memoized function will store the return value for any arguments it has previously received. A second call to fib(25) would not re-compute the return value recursively, but instead return the existing one that has already been constructed.
Memoization can be expressed naturally as a higher-order function, which can also be used as a decorator. The definition below creates a cache of previously computed results, indexed by the arguments from which they were computed. The use of a dictionary requires that the argument to the memoized function be immutable.

>>> def memo(f):
        cache = {}
        def memoized(n):
            if n not in cache:
                cache[n] = f(n)
            return cache[n]
        return memoized

If we apply memo to the recursive computation of Fibonacci numbers, a new pattern of computation evolves, depicted below.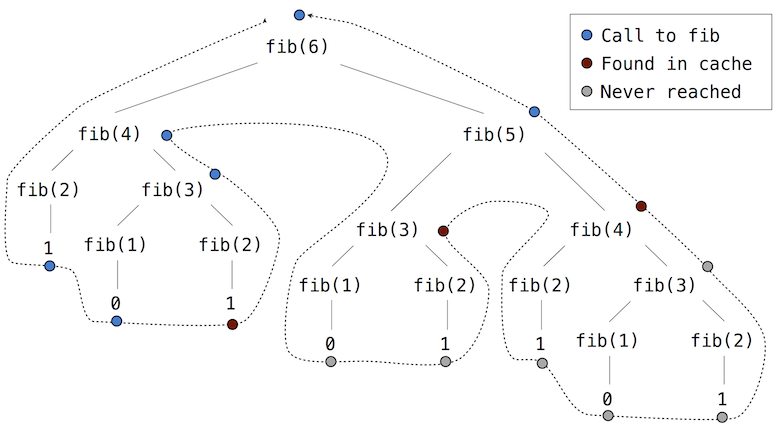

In this computation of fib(5), the results for fib(2) and fib(3) are reused when computing fib(4) on the right branch of the tree. As a result, much of the tree-recursive computation is not required at all.
Using count, we can see that the fib function is actually only called once for each unique input to fib.

>>> counted_fib = count(fib)
>>> fib  = memo(counted_fib)
>>> fib(19)
4181
>>> counted_fib.call_count
20
>>> fib(34)
5702887
>>> counted_fib.call_count
35