备忘录

  1. // 斐波那契数列及其优化
  4. function fibonacci(n) {
  5.     if (n < 1) throw new Error('参数错误');
  7.     if (n === 1 || n === 2) return 1;
  8.     return fibonacci(n - 1) + fibonacci(n - 2);
  9. }
  12. function memo(fn) {
  13.     let obj = {};
  15.     return function(n) {
  16.         if (obj[n] === undefined) obj[n] = fn(n);
  17.         return obj[n];
  18.     }
  19. }

滚动数组方式

  1. const fibo = n => {
  2.     // 判断输入的值是否有效，也可以抛出异常
  3.     if (typeof n !== 'number' || !n) return 0;
  4.     let arr = [1, 1];
  5.     if (n > 2) {
  6.         // 仅当n大于2时需要替换arr中的值
  7.         // 循环的时候将上一次末尾的值替换掉头部的值，而尾部的值则等于上一次数组中两项之和
  8.         for (let i = 3; i <= n; i++) arr = [arr[1], arr[0] + arr[1]];
  9.         return arr[1]; // n项的值
  10.     }
  11.     return 1;
  12. }

3、斐波那契数列通项公式
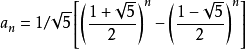
斐波那契数列及其优化 - 图2

  1.      let fib = n => Math.round(
  2.        (Math.pow((1 + Math.sqrt(5)) / 2, n) -
  3.          Math.pow((1 - Math.sqrt(5)) / 2, n)) /
  4.         Math.sqrt(5)
  5.      );

4、矩阵乘法 （高级）

  1. let fib=n=>
  2.   n <= 0
  3.     ? 0
  4.     : martix22_mul(
  5.         [[0, 1], [1, 0]],
  6.         martix22_pow([[0, 1], [1, 1]], n - 1)
  7.       )[0][1];
  9. let martix22_mul = (x, y) => [
  10.   [
  11.     x[0][0] * y[0][0] + x[0][1] * y[1][0],
  12.     x[0][0] * y[0][1] + x[0][1] * y[1][1]
  13.   ],
  14.   [x[1][0] * y[0][0] + x[1][1] * y[1][0], x[1][0] * y[0][1] + x[1][1] * y[1][1]]
  15. ];
  17. let martix22_pow = (x, n) => {
  18.   let r = [[1, 0], [0, 1]];
  19.   let v = x;
  20.   while (n) {
  21.     if (n % 2 == 1) {
  22.       r = martix22_mul(r, v);
  23.       n -= 1;
  24.     }
  25.     v = martix22_mul(v, v);
  26.     n = n / 2;
  27.   }
  28.   return r;
  29. };

推理过程：https://www.jianshu.com/p/adca358b6ec2