• 掌握 HashMap 的基本数据结构
  • 掌握树化
  • 理解索引计算方法、二次 hash 的意义、容量对索引计算的影响
  • 掌握 put 流程、扩容、扩容因子
  • 理解并发使用 HashMap 可能导致的问题
  • 理解 key 的设计

底层数据结构

1.7 和 1.8 有什么不同？

  • 1.7 数组 + 链表
  • 1.8 数组 + （链表 | 红黑树）

树化与退化

为何要用红黑树，为何不一上来不树化，树化阈值为何是8，何时会树hua，何时会退化为链表？

  1. 查询效率：链表短时没必要树化，查询效率跟树化差不多
  2. 所占空间：树节点存储空间 > 链表节点存储空间

为啥要进行链表转红黑树？

为了提高查询速度，如果没有链表转红黑树，当数组某个下标的链表非常长，查询是非常慢的。

解决链表过长思路？

  1. 扩容，将链表的元素分散（当 hash 值重复不高，如果计算的hash 值都一样，无论扩容多少次，链表还是非常长的），当前元素个数是数组的 3/4 时才进行扩容

    1. 扩容的时候，链表的每个元素都会重新计算 hash 值，并放到新的位置上

  2. 链表转红黑树

  • 红黑树用来避免 DoS 攻击（构造一大批 hash 一样），防止链表超长时性能下降，树化应当是偶然情况，是保底策略，树化是万不得已的时候才触发
    • hash 表的查找，更新的时间复杂度是 HashMap - 图1#card=math&code=O%281%29&id=eFasl)，而红黑树的查找，更新的时间复杂度是 HashMap - 图2#card=math&code=O%28log_2%E2%81%A1n%20%29&id=FH8hg)，TreeNode 占用空间也比普通 Node 的大，如非必要，尽量还是使用链表
    • hash 值如果足够随机，则在 hash 表内按泊松分布，在负载因子 0.75 的情况下，长度超过 8 的链表出现概率是 0.00000006，树化阈值选择 8 就是为了让树化几率足够小
  • 当链表长度超过树化阈值 8 时，先尝试扩容来减少链表长度，如果数组容量已经 >=64，才会进行树化
  • 链表的长度是能超过 8 的（当数组容量 <64 且新插入的元素的hash值和链表上元素相同时）
  • 树化两个条件**链表长度 > 8** 和**数组容量 >= 64**
  • 退化规则
    • 情况1：在扩容时如果拆分树时，树元素个数 <= 6 则会退化链表
    • 情况2：remove 树节点时，若 root、root.left、root.right、root.left.left 有一个为 null ，也会退化为链表
  1. 扩容（加载）因子为何默认是 0.75f
  • 在空间占用与查询时间之间取得较好的权衡
  • 大于这个值，空间节省了，但链表就会比较长影响性能
  • 小于这个值，冲突减少了，但扩容就会更频繁，空间占用也更多

    索引计算

索引如何计算？hashCode 都有了，为何还要提供 hash() 方法？数组容量为何是 2 的 n 次幂？

  1. 索引计算方法
  • 首先，计算对象的 hashCode()
  • 再进行调用 HashMap 的 hash() 方法进行二次哈希
    • 二次 hash() 是为了综合高位数据，让哈希分布更为均匀
  • 最后 & (capacity – 1) 得到索引
  1. 数组容量为何是 2 的 n 次幂
  2. 计算索引时效率更高：如果是 2 的 n 次幂可以使用位与运算（&）代替取模（%）
  3. 数组扩容时重新计算索引效率更高： 插入的元素发生扩容时，会分成两个链表（hash & oldCap == 0 和 hash & oldCap 1= 0），然后这两个链表的元素，批量操作放到扩容后数组的新位置
    1. hash & oldCap == 0 的元素：留在原来位置
    2. hash & oldCap != 0 的元素：新位置 = 旧位置 + oldCap

  4. 数组容量为 2 的 n 次幂问题：如果插入的元素都是偶数，那么偶数&2的n次幂永远都是偶数，这样会导致奇数的桶没有元素

    1. 追求每次计算索引的效率：选择数组容量为 2 的 n 次幂
    2. 追求hash分布性：选择数组容量为奇数的，甚至都可以不用2次hash（一次就可以）
    3. hashTable 的数组容量就不是 2的n次幂

  5. 为啥要 2 次 hash

  • 虽然 2 次 hash 增加了计算量，但它防止超长链表的产生
  • 第一次 hash 使用数值的地位，容易造成 hash 值相同，分布不均，而第二次hash ，利用数值高位，计算 hash，使其分布均匀
    1. /**
    2. * Computes key.hashCode() and spreads (XORs) higher bits of hash
    3. * to lower.  Because the table uses power-of-two masking, sets of
    4. * hashes that vary only in bits above the current mask will
    5. * always collide. (Among known examples are sets of Float keys
    6. * holding consecutive whole numbers in small tables.)  So we
    7. * apply a transform that spreads the impact of higher bits
    8. * downward. There is a tradeoff between speed, utility, and
    9. * quality of bit-spreading. Because many common sets of hashes
    10. * are already reasonably distributed (so don't benefit from
    11. * spreading), and because we use trees to handle large sets of
    12. * collisions in bins, we just XOR some shifted bits in the
    13. * cheapest possible way to reduce systematic lossage, as well as
    14. * to incorporate impact of the highest bits that would otherwise
    15. * never be used in index calculations because of table bounds.
    16. */
    17. static final int hash(Object key) {
    18.   int h;
    19.   return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    20. }

put 扩容


  1. HashMap 是懒惰创建数组的，首次使用才创建数组
  2. 计算索引（桶下标）
  3. 如果桶下标还没人占用，创建 Node 占位返回
  4. 如果桶下标已经有人占用
    1. 已经是 TreeNode 走红黑树的添加或更新逻辑
    2. 是普通 Node，走链表的添加或更新逻辑，如果链表长度超过树化阈值，走树化逻辑
  5. 返回前检查容量是否超过阈值，一旦超过进行扩容

jdk 1.8 put 时，先将新的元素插入到旧数组中，然后再进行扩容，计算桶下表

1.7 与 1.8 的区别

  1. 链表插入节点时，1.7 是头插法，1.8 是尾插法
  2. 1.7 是大于等于阈值且没有空位时才扩容，而 1.8 是大于阈值就扩容
  3. 1.8 在扩容计算 Node 索引时，会优化

并发问题

  1. 容易造成数据丢失问题（1.7 ｜ 1.8）
  2. 扩容死链（1.7）
  1. public static void main(String[] args) throws InterruptedException {
  4.     // 97 和 49 计算 hash 都是 1
  5.     // 97%16 = 1    49%16 = 1
  6.     // 要在 HashMap 中 putVal() 打断点
  7.     HashMap<String, Object> map = new HashMap<>();
  8.     Thread t1 = new Thread(() -> {
  9.         map.put("a", new Object()); // 97  => 1
  10.     }, "t1");
  12.     Thread t2 = new Thread(() -> {
  13.         map.put("1", new Object()); // 49 => 1
  14.     }, "t2");
  16.     t1.start();
  17.     t2.start();
  18.     t1.join();
  19.     t2.join();
  20.     System.out.println(map);
  21. }

debug 调试：
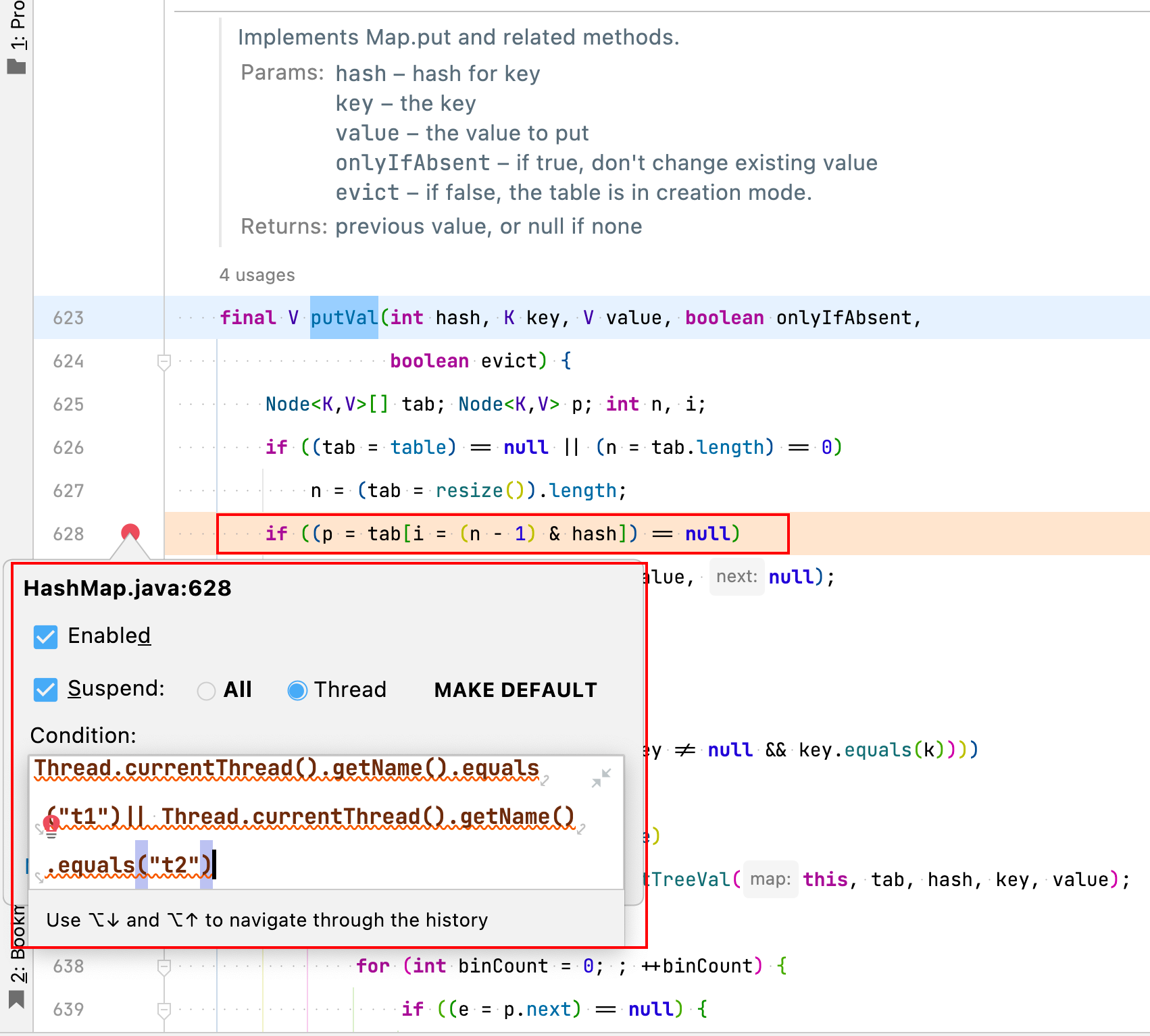
image.png

key 要求

key 能否为null，作为 key 的对象有什么要求？

  1. HashMap 的 key 可以为 null，其它 Map 的 key 不能为 null（会报空指针异常）
  2. 作为 key 的对象，必须重写 hashCode() 和 equals()
    1. 重写 hashCode()：目的是 key 在 HashMap 中有更好的分布性，提高查询性能
    2. 重写 equals()：当两个元素计算的索引相同时，用 equals 进行判断元素内容是否相同
      1. hashCode 相同时，equals 不一定相同
      2. equals 相同时，hashCode 一定相同
    3. key 一定是个不可变对象，要不然会发生找不到

String 中 hashCode

String 中 hashCode() 如何设计的，为啥每次乘的都是 31？

  • 目标是达到较为均匀的散列效果，每个字符串的 hashCode 足够独特
  • 字符串中的每个字符都可以表现为一个数字，称为 HashMap - 图4，其中 i 的范围是 0 ~ n - 1
  • 散列公式为： HashMap - 图5%7D%2B%20S1%E2%88%9731%5E%7B(n-2)%7D%2B%20%E2%80%A6%20S_i%20%E2%88%97%2031%5E%7B(n-1-i)%7D%2B%20%E2%80%A6S%7B(n-1)%7D%E2%88%9731%5E0#card=math&code=S0%E2%88%9731%5E%7B%28n-1%29%7D%2B%20S_1%E2%88%9731%5E%7B%28n-2%29%7D%2B%20%E2%80%A6%20S_i%20%E2%88%97%2031%5E%7B%28n-1-i%29%7D%2B%20%E2%80%A6S%7B%28n-1%29%7D%E2%88%9731%5E0&id=CJxWP)
  • 31 代入公式有较好的散列特性，并且 31 * h 可以被优化为
    • 即 32 ∗ h - h
    • 即 HashMap - 图6
    • 即 HashMap - 图7