二叉树有多种遍历方法，有层次遍历、深度优先遍历、广度优先遍历等。
本文只涉及二叉树的先序、中序、后序的递归和非递归遍历。
涉及到的代码都用Java编写。

首先给出二叉树节点类：

树节点：

  1. class TreeNode {
  2.     int val;
  3.     //左子树
  4.     TreeNode left;
  5.     //右子树
  6.     TreeNode right;
  7.     //构造方法
  8.     TreeNode(int x) {
  9.         val = x;
  10.     }
  11. }

无论是哪种遍历方法，考查节点的顺序都是一样的(思考做试卷的时候，人工遍历考查顺序)。只不过有时候考查了节点，将其暂存，需要之后的过程中输出。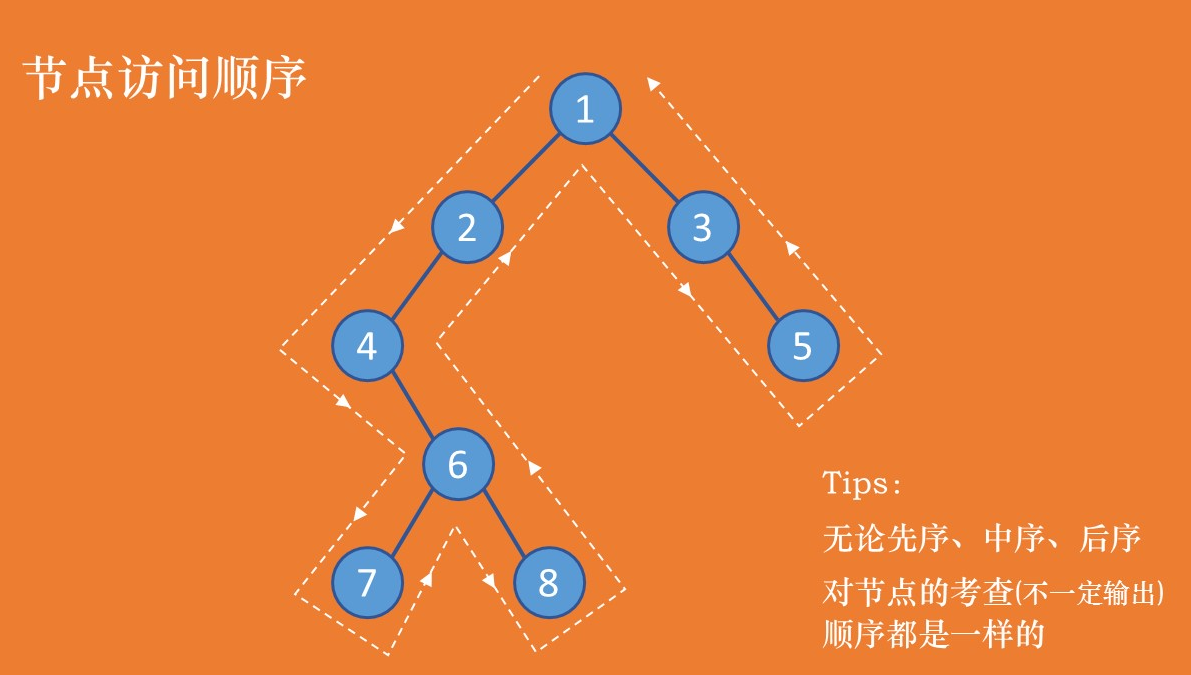
image.png
图1：先序、中序、后序遍历节点考查顺序
如图1所示，三种遍历方法(人工)得到的结果分别是：
先序：1 2 4 6 7 8 3 5
中序：4 7 6 8 2 1 3 5
后序：7 8 6 4 2 5 3 1
三种遍历方法的考查顺序一致，得到的结果却不一样，原因在于：
先序：考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右)
中序：考察到一个节点后，将其暂存，遍历完左子树后，再输出该节点的值，然后遍历右子树。(左根右)
后序：考察到一个节点后，将其暂存，遍历完左右子树后，再输出该节点的值。(左右根)

先序遍历

递归先序遍历

递归先序遍历很容易理解，先输出节点的值，再递归遍历左右子树。中序和后序的递归类似，改变根节点输出位置即可。

  1. // 递归先序遍历
  2. public static void recursionPreorderTraversal(TreeNode root) {
  3.     if (root != null) {
  4.         System.out.print(root.val + " ");
  5.         recursionPreorderTraversal(root.left);
  6.         recursionPreorderTraversal(root.right);
  7.     }
  8. }

非递归先序遍历

因为要在遍历完节点的左子树后接着遍历节点的右子树，为了能找到该节点，需要使用栈来进行暂存。中序和后序也都涉及到回溯，所以都需要用到栈。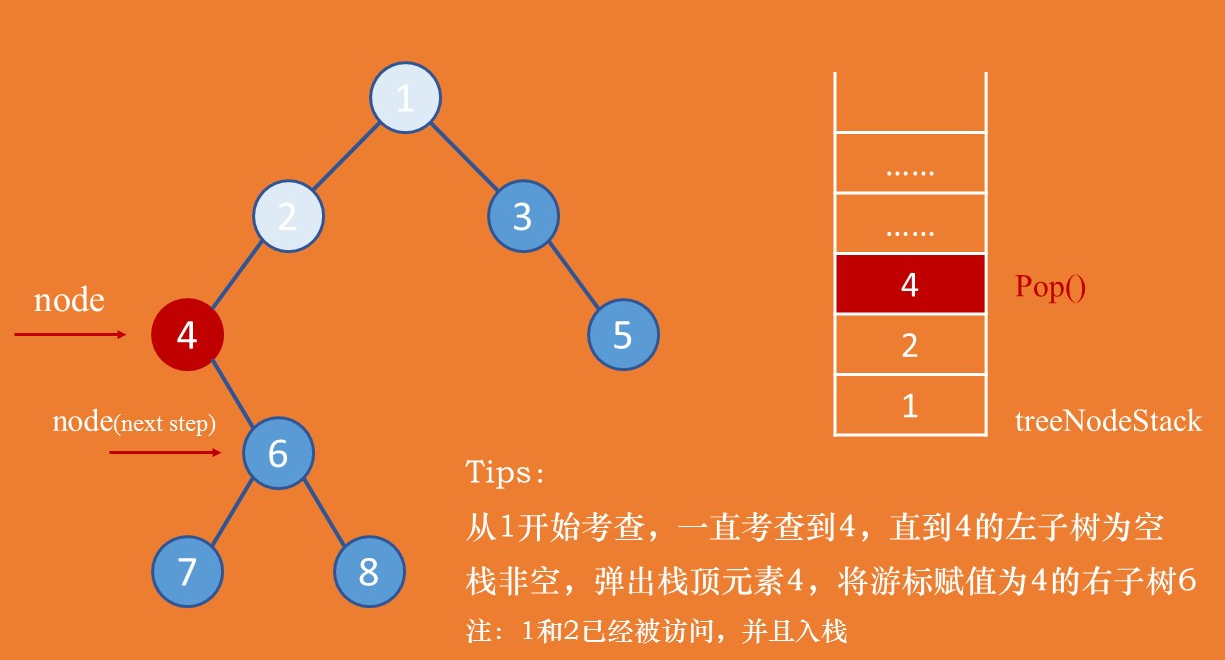
image.png
图2：非递归先序遍历
遍历过程参考注释

  1. // 非递归先序遍历
  2. public static void preorderTraversal(TreeNode root) {
  3.     // 用来暂存节点的栈
  4.     Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
  5.     // 新建一个游标节点为根节点
  6.     TreeNode node = root;
  7.     // 当遍历到最后一个节点的时候，无论它的左右子树都为空，并且栈也为空
  8.     // 所以，只要不同时满足这两点，都需要进入循环
  9.     while (node != null || !treeNodeStack.isEmpty()) {
  10.         // 若当前考查节点非空，则输出该节点的值
  11.         // 由考查顺序得知，需要一直往左走
  12.         while (node != null) {
  13.             System.out.print(node.val + " ");
  14.             // 为了之后能找到该节点的右子树，暂存该节点
  15.             treeNodeStack.push(node);
  16.             node = node.left;
  17.         }
  18.         // 一直到左子树为空，则开始考虑右子树
  19.         // 如果栈已空，就不需要再考虑
  20.         // 弹出栈顶元素，将游标等于该节点的右子树
  21.         if (!treeNodeStack.isEmpty()) {
  22.             node = treeNodeStack.pop();
  23.             node = node.right;
  24.         }
  25.     }
  26. }

先序遍历结果：

递归先序遍历： 1 2 4 6 7 8 3 5
非递归先序遍历：1 2 4 6 7 8 3 5

中序遍历

递归中序遍历

过程和递归先序遍历类似

  1. // 递归中序遍历
  2. public static void recursionMiddleorderTraversal(TreeNode root) {
  3.     if (root != null) {
  4.         recursionMiddleorderTraversal(root.left);
  5.         System.out.print(root.val + " ");
  6.         recursionMiddleorderTraversal(root.right);
  7.     }
  8. }

非递归中序遍历

和非递归先序遍历类似，唯一区别是考查到当前节点时，并不直接输出该节点。
而是当考查节点为空时，从栈中弹出的时候再进行输出(永远先考虑左子树，直到左子树为空才访问根节点)。

  1. // 非递归中序遍历
  2. public static void middleorderTraversal(TreeNode root) {
  3.     Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
  4.     TreeNode node = root;
  5.     while (node != null || !treeNodeStack.isEmpty()) {
  6.         while (node != null) {
  7.             treeNodeStack.push(node);
  8.             node = node.left;
  9.         }
  10.         if (!treeNodeStack.isEmpty()) {
  11.             node = treeNodeStack.pop();
  12.             System.out.print(node.val + " ");
  13.             node = node.right;
  14.         }
  15.     }
  16. }

中序遍历结果

递归中序遍历： 4 7 6 8 2 1 3 5
非递归中序遍历：4 7 6 8 2 1 3 5

后序遍历

递归后序遍历

过程和递归先序遍历类似

  1. // 递归后序遍历
  2. public static void recursionPostorderTraversal(TreeNode root) {
  3.     if (root != null) {
  4.         recursionPostorderTraversal(root.left);
  5.         recursionPostorderTraversal(root.right);
  6.         System.out.print(root.val + " ");
  7.     }
  8. }

非递归后序遍历

后续遍历和先序、中序遍历不太一样。
后序遍历在决定是否可以输出当前节点的值的时候，需要考虑其左右子树是否都已经遍历完成。
所以需要设置一个lastVisit游标。
若lastVisit等于当前考查节点的右子树，表示该节点的左右子树都已经遍历完成，则可以输出当前节点。
并把lastVisit节点设置成当前节点，将当前游标节点node设置为空，下一轮就可以访问栈顶元素。
否者，需要接着考虑右子树，node = node.right。
以下考虑后序遍历中的三种情况：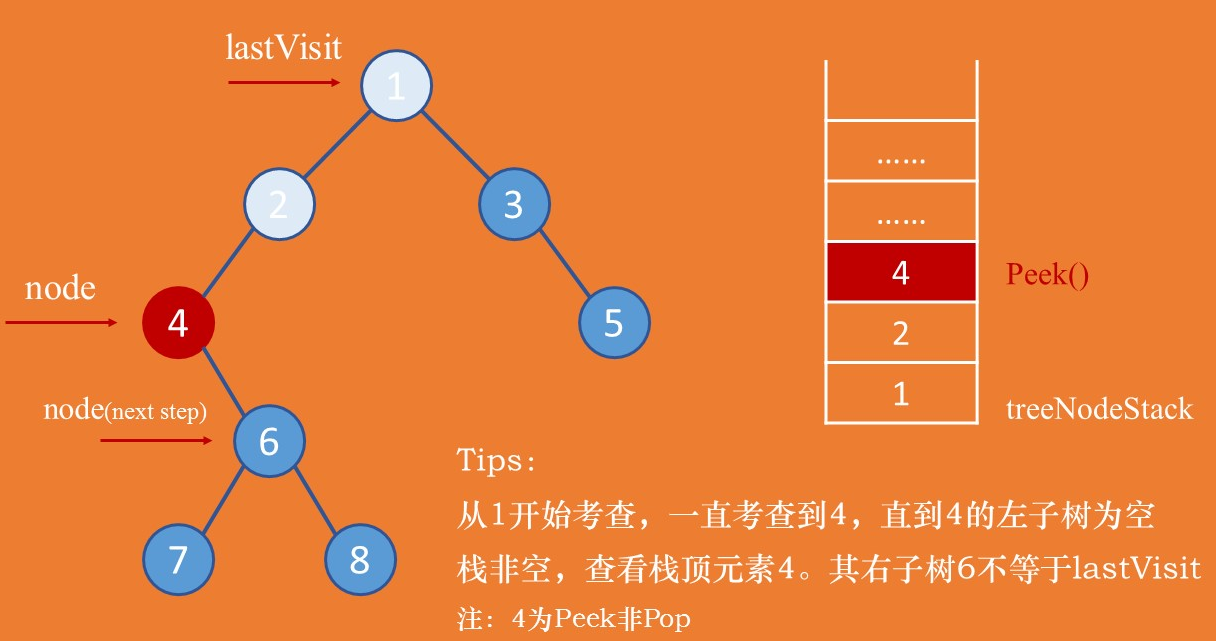
image.png图3：后序，右子树不为空，node = node.right
如图3所示，从节点1开始考查直到节点4的左子树为空。
注：此时的游标节点node = 4.left == null。
此时需要从栈中查看 Peek()栈顶元素。
发现节点4的右子树非空，需要接着考查右子树，4不能输出，node = node.right。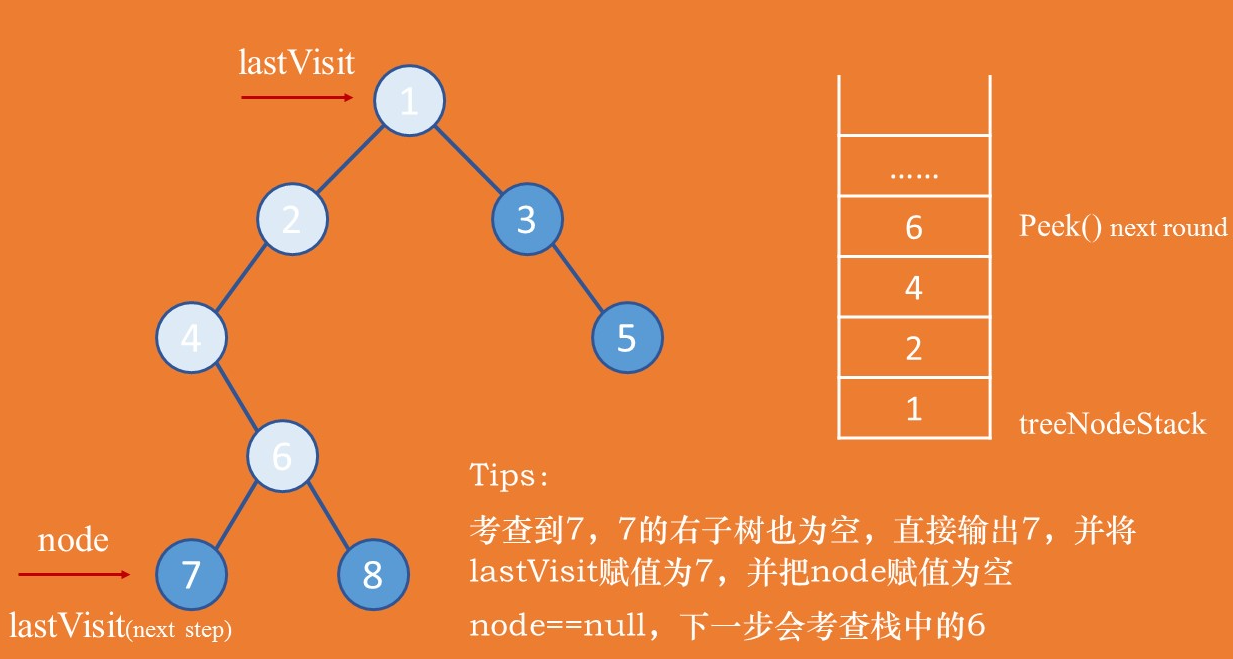
image.png
图4：后序，左右子树都为空，直接输出
如图4所示，考查到节点7(7.left == null，7是从栈中弹出)，其左右子树都为空，可以直接输出7。
此时需要把lastVisit设置成节点7，并把游标节点node设置成null，下一轮循环的时候会考查栈中的节点6。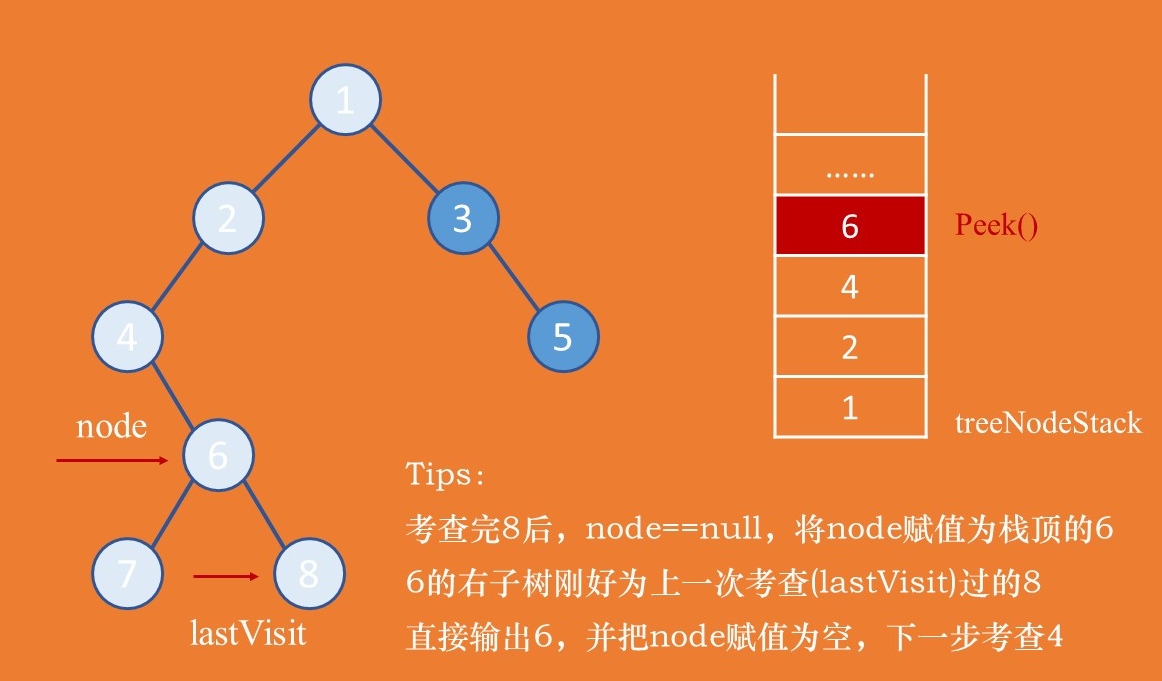
image.png
图5：后序，右子树 = lastVisit，直接输出
如图5所示，考查完节点8之后(lastVisit == 节点8)，将游标节点node赋值为栈顶元素6，节点6的右子树正好等于节点8。表示节点6的左右子树都已经遍历完成，直接输出6。
此时，可以将节点直接从栈中弹出Pop()，之前用的只是Peek()。
将游标节点node设置成null。

  1. // 非递归后序遍历
  2. public static void postorderTraversal(TreeNode root) {
  3.     Stack<TreeNode> treeNodeStack = new Stack<TreeNode>();
  4.     TreeNode node = root;
  5.     TreeNode lastVisit = root;
  6.     while (node != null || !treeNodeStack.isEmpty()) {
  7.         while (node != null) {
  8.             treeNodeStack.push(node);
  9.             node = node.left;
  10.         }
  11.         //查看当前栈顶元素
  12.         node = treeNodeStack.peek();
  13.         //如果其右子树也为空，或者右子树已经访问
  14.         //则可以直接输出当前节点的值
  15.         if (node.right == null || node.right == lastVisit) {
  16.             System.out.print(node.val + " ");
  17.             treeNodeStack.pop();
  18.             lastVisit = node;
  19.             node = null;
  20.         } else {
  21.             //否则，继续遍历右子树
  22.             node = node.right;
  23.         }
  24.     }
  25. }

后序遍历结果

递归后序遍历： 7 8 6 4 2 5 3 1
非递归后序遍历：7 8 6 4 2 5 3 1