概念
进制也就是进位制,是人们规定的一种进位方法。 对于任何一种进制—-X进制,就表示某一位置上的数运算时是逢X进一位。
- 十进制是逢十进一
- 十六进制是逢十六进一
- 二进制就是逢二进一
以此类推,x进制就是逢x进位。
进位制/位置计数法是一种记数方式,故亦称进位记数法/位值计数法,可以用有限的数字符号代表所有的数值。
可使用数字符号的数目称为基数(en:radix)或底数,基数为n,即可称n进位制,简称n进制。
现在最常用的是十进制,通常使用10个阿拉伯数字0-9进行记数。
对于任何一个数,我们可以用不同的进位制来表示。比如:十进数57(10),可以用二进制表示为111001(2),也可以用五进制表示为212(5),也可以用八进制表示为71(8)、用十六进制表示为39(16),它们所代表的数值都是一样的。
进制由来
二进制由来
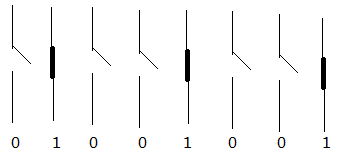
由于两个开关状态表示的数据有限,所以国际化组织规定了由8个状态来表示一个数据。作为一个数据的基本单位。随着后来的发展,我们采用数字信号替代了电信号,分别用1和0来表示开关。
8个1和0这样的数据就是计算机存储的最基本单位,叫字节 byte
1和0这样的数据叫比特位, bit
1byte=8bit1k=1024byte 10^51m=1024k1g=1024m1t=1024g
二进制只有0和1两个数字,基数为2,在加减法运算中,逢二进一,借一当二。
表示数值:0、1、10、111、100、1000001
加法:1+0=1、1+1=10、10+110=1000、111+111=1110、
减法:1-0=1、10-1=1、100-11=1、1010-101=101
八进制表示
把上图中的二进制数据,按照从右到左每三位一组合,然后计算出该三个组合数据的十进制数值,在把十进制的数组合到一起,就形成了八进制。
注意:如果位数不够,在左边补齐0
所以上图中 01001001 八进制表示如下图,由于位数不够在最左边补了0

十六进制表示
发现八进制还是有点大,就出现十六进制
把二进制的数据,按照从右到左每四位一组合,然后计算出该四个组合数据的十进制数值,在把十进制的数组合到一起,就形成了十六进制。

总结
从上面三个图中可以看出:进制越大,表示形式越短
进制一览
- 二进制数
组成:由0,1组成。用0b开头表示(是数字0不是字母o)。0b1011 => 11
- 四进制
- 七进制数
- 八进制数
由0-7组成。用0开头表示。013 =>11
- 十进制数
由0-9组成。默认整数就是十进制。 11
- 十二进制
- 十六进制
由0-9,a-f(不区分大小写)。用0x开头表示 0xb => 11
在c语言中0x表示小写a-f 0X表示大写A-F
这里主要总结: 二进制 八进制 十六进制 十进制
//如十进制 11console.log(0b1011) //二制进0b1011 打印出11console.log(013) //二制进013 打印出11console.log(0xb) //十六制进0xb 打印出11
从其他进制到十进制的转换
总结
- 系数:某个数据的每一位数据就是该位上的系数,如表格12345系数就是: 1 2 3 4 5
- 基数:X进制的基数就是X, 如:十进制基数10 , 二进制基数2 ,八进制基数8
- 权:把某个数的每一位上的数从右往左进行编号,而是从0开始,把每个编号看成该数据的权,如表格12345从右往左数就是:0 1 2 3 4,如有负数就是 -1 -2
结论: 系数 * 基数的权次幂之和
365 的系数是: 3 6 5 ,基数是:10 , 权是:0 1 2
365 = 3 10^2 + 6 10^1 + 5 * 10^0
= 300 + 60 + 5= 365
十进制到十进制
| 十进制 | 十进制 |
|---|---|
| 12345 | 10000 + 2000 + 300 + 40 + 5 |
| 1_ 10^4 + 2 _10^3 + 3 _10^2 + 4 _10^1 + 5 * 10^0 | |
| 12345 |
12345 系数:1,2,3,4,5 ;基数:10;权:0,1,2,3,4
二进制到十进制
| 二进制 | 十进制 |
|---|---|
| 1011 | 1 2^3 + 0 2^2 + 1 2^1 + 1 2^0 |
| 8 + 0 + 2 + 1 | |
| 11 |
1011 系数:1,0,1,1;基数:2;权:0,1,2,3
八进制到十进制
| 八进制 | 十进制 |
|---|---|
| 1011 | 2 8^2 + 5 8^1 + 6 * 8^0 |
| 128 + 40 + 6 | |
| 174 |
256 系数:2,5,6;基数:8;权:0,1,2
十六进制到十进制
| 十六进制 | 十进制 |
|---|---|
| 3a | 3 _16^1 + 10 _16^0 |
| 48 + 10 | |
| 58 |
3a 系数:3,10;基数:16;权:0,1
注意:十六进制a-f是10-15
十进制到其他进制的转换
规律:除基取余,直到商为0,最合余数反转
十进制到十进制
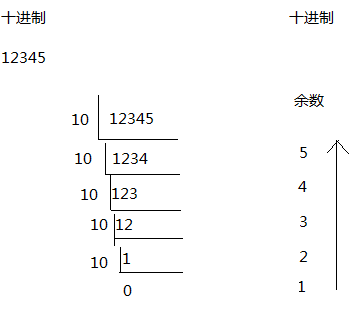
十进制:12345 => 十进制:12345
十进制到二进制
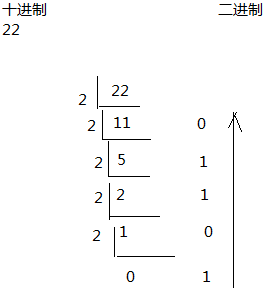
十进制:22 => 二进制:10110
二进制和十进制间快速转换 8421码
8421码中的8421是什么意思?
表示一位十进制数的二进制码的每一位有确定的权一般用8421码
其四个二进制码的权从高到低分别为8,4,2,1.
8421是最常用的二进制码,叫这个是因为四位8421码时,从左到右=每个”1”代表的十进制数分别是”8”、”4”、”2”、”1”
如下:
- 1000 为十进制 8
- 0100 为十进制 4
- 0010 为十进制 2
- 0001 为十进制 1
二进制到十六进制8421转换
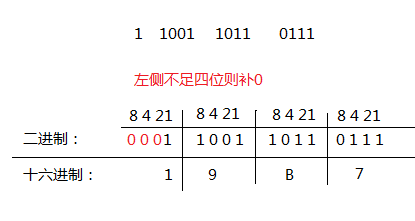
从上图可以看出把系数为有1 进行 8421相加 如9=8+1,B=8+2+1
十进制转二进制快速转换方法:8421
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|
| 1*2^7 | 1*2^6 | 1*2^5 | 1*2^4 | 1*2^3 | 1*2^2 | 1*2^1 | 1*2^0 |
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 十进制 | 二进制 | 八进制 | 十六进制 | 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|---|---|---|---|
| 0 | 0000 | 0 | 0 | 10 | 1010 | 12 | A |
| 1 | 0001 | 1 | 1 | 11 | 1011 | 13 | B |
| 2 | 0010 | 2 | 2 | 12 | 1100 | 14 | C |
| 3 | 0011 | 3 | 3 | 13 | 1101 | 15 | D |
| 4 | 0100 | 4 | 4 | 14 | 1110 | 16 | E |
| 5 | 0101 | 5 | 5 | 15 | 1111 | 17 | F |
| 6 | 0110 | 6 | 6 | 16 | 10000 | 20 | 10 |
| 7 | 0111 | 7 | 7 | 17 | 10001 | 21 | 11 |
| 8 | 1000 | 10 | 8 | 18 | 10010 | 22 | 12 |
| 9 | 1001 | 11 | 9 | 19 | 10011 | 23 | 13 |
二进制到十进制:0101 1110 = 64 +16 + 8 + 4 + 2 = 94
根据上面表格中对应关系有1的算出来如:1110对应的就是 8 4 2
十进制到二进制156如:直接减128
156
-128
28
-16
12
-8
4
-4
156=128+16+8+4= 1001 1100
如300:
300
-256
44
-32
12
-8
4
-4
300=256 + 32 + 8 +4 =1 0010 1100
有符号数据的表示方法:原码 反码 补码
机器数和真值
- 机器数
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。
机器数是带符号的,在计算机用一个数的最高位存放符号, 正数为0, 负数为1。
比如,十进制中的数 +3 ,计算机字长为8位,转换成二进制就是0000 0011。如果是 -3 ,就是 1000 0011 。
那么,这里的 00000011 和 10000011 就是机器数。 - 真值
因为第一位是符号位,所以机器数的形式值就不等于真正的数值。
例如上面的有符号数 10000011,其最高位1代表负,其真正数值是 -3 而不是形式值131(10000011转换成十进制等于131)。
所以,为区别起见,将带符号位的机器数对应的真正数值称为机器数的真值。
例:0000 0001的真值 = +000 0001 = +1,1000 0001的真值 = –000 0001 = –1
| 符号位 | 数值位 | 真值 | |
|---|---|---|---|
| +1 | 0 | 0000001 | +1 |
| -1 | 1 | 0000001 | -1 |
原码
把数据按照符号位和数值位分开,最高位为符号位,正数用0,负数用1
| 符号位 | 数值位 | |
|---|---|---|
| +7 | 0 | 0000111 |
| -7 | 1 | 0000111 |
| 符号位 | 数值位 | |
|---|---|---|
| +1 | 0 | 0000001 |
| -1 | 1 | 0000001 |
第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即 64+32+16+8+4+2+1=127
[-127 , 127]
反码
正数的反码和原码相同。
负数的反码和原码的区别是:符号位不变,数值位0变1,1变0
| 符号位 | 数值位 | |
|---|---|---|
| +7 | 0 | 0000111 |
| -7 | 1 | 1111000 |
补码
正数的补码和原码相同。
负数的补码是反码+1
| 符号位 | 数值位 | |
|---|---|---|
| +7 | 0 | 0000111 |
| -7 | 1 | 1111001 |
示例
1. 计算1-1的值是多少?
数值位相加是:1 0000010 ,两个1相加是缝2进1,按原码计算发现结果是-2,因为计算机底层所有存储和计算机都是以补码形式存在的。
用补码计算:
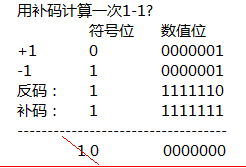
从图中可以看出原码和补码相加
原码 0 0000001
补码 0 0000001
结果 10 0000000
符号位有益出,要舍弃1,所以最终结果是0
已知原码10110100,求反码和补码
| 符号位 | 数值位 | |
|---|---|---|
| 原码 | 1 | 0110100 |
| 反码 | 1 | 1001011 |
| 补码 | 1 | 1001100 |
已知补码11101110,求原码
| 符号位 | 数值位 | |
|---|---|---|
| 补码 | 1 | 1101110 |
| 反码 | 1 | 1101101 |
| 原码 | 1 | 0010010 |
注:负数的补码到反码是-1

