一、基本的概念

图：表示多对多的关系。是一种数据结构，其中的节点可以包含零个或者多个节点，两个节点之间的连接称为边，节点也称之为顶点。
图分为无向图、有向图、带权图。
图的表示方式：二维数组表示（邻接矩阵），链表表示（邻接表）
邻接矩阵：表示图形中顶点之间的相邻关系的矩阵，对于n个顶点关系的矩阵，矩阵是nn的
邻接表：邻接表只关心存在的边，不关心不存在的边，因此没有浪费空间，使用*数组与链表实现。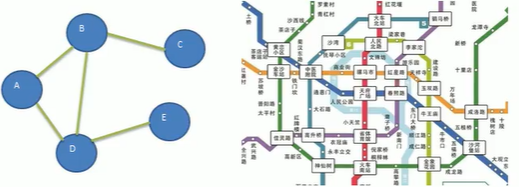
image-20210117110947131.png

二、图的遍历

2.1 深度优先

深度优先遍历（DFS）：从初始访问点出发，初始访问节点可能有多个邻接节点，深度优先遍历的策略是首先访问第一个临接点，然后再以这个被访问的邻接节点作为初始节点，继续访问它的第一个邻接节点，直到访问到最后为止。然后再访问第二节点。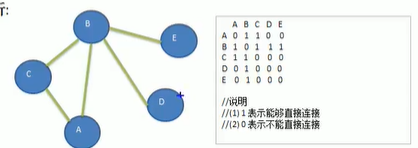
image-20210117114943902.png
算法步骤：

  1. 访问初始节点v，并且标记节点v已经访问
  2. 查找节点v的第一个临界点w
  3. 如果w存在，则继续执行4；如果w不存在，则返回1，将从v的下一个节点继续
  4. 如果w未被访问，则对w进行深度优先遍历递归（把w看做是v，然后递归执行123）
  5. 查找节点v的w邻接节点的下一个邻接节点，转到步骤3

代码的实现：

  1. /**
  2.      * 获取第一个邻接节点
  3.      * @param index
  4.      * @return
  5.      */
  6. public int getFirstNeigbor(int index) {
  7.     for(int i=0; i<vertextList.size(); i++) {
  8.         //            if(!isVisited[i])
  9.         if(edges[index][i] > 0) return i;
  10.     }
  12.     return -1;
  13. }
  15. /**
  16.      * 获取从n后的第一个邻接节点
  17.      * @param index 表示访问第index个节点
  18.      * @param n    从第n个位置开始访问
  19.      * @return
  20.      */
  21. public int getOtherNeigbor(int index, int n) {
  22.     for(int i=n+1; i<vertextList.size(); i++) {
  23.         if(edges[index][i] > 0) return i;
  24.     }
  25.     return -1;
  26. }
  28. /**
  29.      * 深度优先遍历
  30.      * @param isVisited 布尔数组，存储节点是否被访问过
  31.      * @param i    当前遍历的节点的位置
  32.      */
  33. public void dfs(boolean[] isVisited, int i) {
  34.     // 输出第i个节点
  35.     System.out.print(getVertexByIndex(i) + "->");
  36.     // 将该位置标记为已访问
  37.     isVisited[i] = true;
  38.     // 获取该位置的第一个邻接节点
  39.     int w = getFirstNeigbor(i);
  40.     // 如果w存在，则进行递归深度遍历
  41.     while(w != -1) {
  42.         // 如果w位置的节点没有被访问过，则进行深度递归
  43.         if(!isVisited[w]) {
  44.             dfs(isVisited, w);
  45.         }
  47.         // 然后继续进行查找相邻的邻接节点
  48.         w = getOtherNeigbor(i, w);
  49.     }
  50. }
  52. /**
  53.      * 深度优先遍历
  54.      */
  55. public void dfs() {
  56.     isVisited = new boolean[vertextList.size()];
  57.     for(int i=0; i<vertextList.size(); i++) {
  58.         // 如果该节点没有被访问过，则进行深度遍历
  59.         if(!isVisited[i]) {
  60.             dfs(isVisited, i);
  61.         }
  62.     }
  63.     System.out.println();
  64. }

2.2 广度优先

广度优先遍历（BFS）：广度遍历需要一个队列来保存已经访问过的节点的顺序，以便按照这个顺序来访问这些节点的相邻节点。

算法步骤：

  1. 访问初始节点v，并且标记节点v已经访问
  2. 节点v入队列
  3. 当位列为非空时，则继续执行，否则算法结束
  4. 出队列，取得都头节点u
  5. 查找节点u的第一个邻接点w

  6. 如果u的邻接点不存在，则转到步骤3；否则执行以下的三个步骤：

    1. 若是节点w未被访问，则访问节点w并标记为已经访问
    2. 节点w加入队列
    3. 查找节点u的继w邻接点后的下一个邻接点w，转到步骤6


    代码的实现： ```java /**

  • 广度优先遍历算法 */ public void bfs() { // 标记顶点访问 isVisited = new boolean[vertextList.size()]; // 队列存储同一层的节点 Queue list = new LinkedList<>(); // 遍历所有的节点，防止有节点为独立节点，不与其他节点相连 for(int i=0; i<vertextList.size(); i++) {
    1.   // 判断该节点是否被访问过，如果被访问过就直接进行下一个
    2.   if(!isVisited[i]) {
    3.       // 打印节点
    4.       System.out.print(getVertexByIndex(i) + "->");
    5.       list.offer(i);    // 将当前节点添加到队列中
    6.       isVisited[i] = true; // 将输出的节点标记为已访问
    7.       while(!list.isEmpty()) {
    8.           int k = list.poll();    // 队列抛出节点，遍历该节点相连的相邻节点
    9.           for(int j =0; j<k; j++) {
    10.               if(!isVisited[k] && edges[k][j] > 0) {
    11.                   System.out.print(getVertexByIndex(j) + "->");
    12.                   isVisited[j] = true;
    13.               }
    14.           }
    15.       }
    16.   }
    }
    System.out.println(); } ```

三、图的算法

普里姆算法

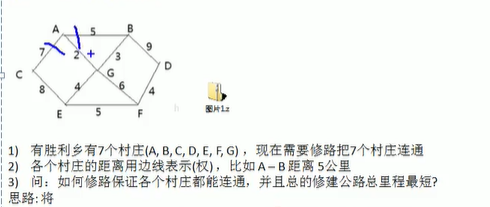
image-20210119195128788.png
正确思路是：就是尽可能的选择少的路线，并且每条路线最小，保证总里程数最小。
修路的问题就是最小生成树问题。
最小生成树，简称MST：

  • 给定一个带权的无向连通图，如何选择一颗生成树，使得树上所有边上权的总和为最小，这就叫做最小生成树。
  • N个顶点，一定有N-1条边
  • 包括全部的顶点
  • N-1条边都在图中

普里姆算法求最小生成树，也就是在包含n个顶点的连通图中，找出(n-1)条边包含所有的n个顶点的连通子图，也就是所谓的极小连通子图。

算法步骤为：

  1. 设G=(V,E)是连通图，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合
  2. 若从顶点u开始构建最小生成树，则从集合v中取出顶点u放入到集合U中，标记顶点v的visited[v]=1
  3. 若集合U中的顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中的权值最小的边，但不能构成回路，将顶点vj加入到集合U中，将边(ui, vj)加入到集合D中，并标记visited[vj]=1
  4. 重复步骤2，直到U与V完全相等，即所有的顶点都被访问过了，此时D中有n-1条边。

迪杰拉斯特算法

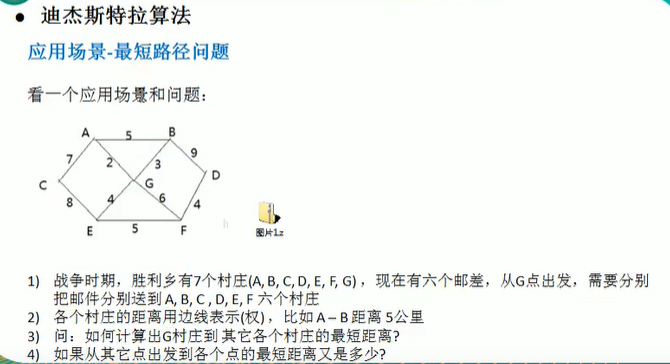
image-20210120102814501.png

迪杰斯特拉算法是典型的最短路径算法，用于计算一个节点到其他节点的最短路径。它的主要特点是以起始点为中心，向外层层扩散（广度优先搜索思想），直到扩展到终点为止。
image-20210120103207060.png
迪杰斯塔拉算法算法的步骤：

  1. 首先给定出发点为index，设置dis[]数组存储节点到出发点的距离，alreadyArr[]数组为该点是否已经访问，preArr为该点的上一个节点。
  2. 从index节点出发，遍历从index点能够到达的点j；如果j点的距离+index点到出发点的距离小于已经存在的j节点或者该j点的距离dis为空，将dis[]数组中j点的位置距离设置为j点的距离+index点到出发点的距离。设置该j点的preArr为index。继续遍历其他的节点。
  3. 继续遍历，寻找alreadyArr[]数组中未遍历的节点，取未遍历节点中距离dis[k]最小的节点作为index节点，然后重复步骤2,3。直到alreaArr[]数组中的节点全部遍历完成。
  4. 输出最后的结果

代码的实现：

  1. public class DijkstraAlgorithm {
  2.     // 迪杰斯塔拉算法
  3.     public static void main(String[] args) {
  4.         char[] point = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
  5.         int[][] matrix = new int[point.length][point.length];
  6.         final int N = -1;
  7.         matrix[0] = new int[]{0, 5, 7, N, N, N, 2};
  8.         matrix[1] = new int[]{5, 0, N, 9, N, N, 3};
  9.         matrix[2] = new int[]{7, N, 0, N, 8, N, N};
  10.         matrix[3] = new int[]{N, 9, N, 0, N, 4, N};
  11.         matrix[4] = new int[]{N, N, 8, N, 0, 5, 4};
  12.         matrix[5] = new int[]{N, N, N, 4, 5, 0, 6};
  13.         matrix[6] = new int[]{2, 3, N, N, 4, 6, 0};
  15.         // 创建迪杰斯塔拉算法对象，设置初始点位置为G
  16. //        Dijkstra dijkstra = new Dijkstra(point.length, 6);
  17.         Dijkstra dijkstra = new Dijkstra(point.length, 0);
  18.         dijkstra.addPoint(point);
  19.         dijkstra.addMatrix(matrix);
  20.         dijkstra.djs();
  21.         dijkstra.show();
  22.     }
  24. }
  26. class Dijkstra{
  27.     char[] point;
  28.     int[][] matrix;
  29.     int pointNum;
  30.     int index;
  31.     Vetext vetext;
  33.     // 构造器
  34.     public Dijkstra(int len, int index) {
  35.         this.pointNum = len;
  36.         this.index = index;
  37.         point = new char[len];
  38.         matrix = new int[len][len];
  39.         vetext = new Vetext(len, index);
  40.     }
  42.     // 添加顶点
  43.     public void addPoint(char[] point) {
  44.         for(int i=0; i<pointNum; i++) {
  45.             this.point[i] = point[i];
  46.         }
  47.     }
  49.     // 添加边的条件
  50.     public void addMatrix(int[][] m) {
  51.         for(int i=0; i<pointNum; i++) {
  52.             for (int j = 0; j < pointNum; j++) {
  53.                 this.matrix[i][j] = m[i][j];
  54.             }
  55.         }
  56.     }
  58.     // 寻找下一个遍历的节点
  59.     public int findNextPoint() {
  60.         int min = Integer.MAX_VALUE;
  61.         int index = 0;
  62.         for(int i=0; i<pointNum; i++) {
  63.             if(vetext.dis[i] != -1 && vetext.alreadArr[i] == 0 && vetext.dis[i] < min) {
  64.                 min = vetext.dis[i];
  65.                 index = i;
  66.             }
  67.         }
  68.         vetext.alreadArr[index] = 1;
  69.         return index;
  70.     }
  72.     /**
  73.      * 更新vetex中的各个数组
  74.      * @param index
  75.      */
  76.     public void updateArr(int index) {
  77.         int len = 0;
  78.         for(int i=0; i<matrix[index].length; i++) {
  79.             if(matrix[index][i] == -1) continue;
  80.             len = matrix[index][i] + vetext.dis[index];
  82.             if((vetext.isDis(i) && len < vetext.dis[i]) || !vetext.isDis(i)) {
  83.                 vetext.dis[i] = len;
  84.                 vetext.prePoint[i] = index;
  85.             }
  86.         }
  87.     }
  89.     /**
  90.      * 迪杰拉斯算法的主要实现过程
  91.      */
  92.     public void djs() {
  93.         for(int i=0; i<pointNum; i++) {
  94.             int index = findNextPoint();
  95.             updateArr(index);
  96.         }
  97.     }
  99.     /**
  100.      * 将数组进行打印
  101.      */
  102.     public void show() {
  103.         vetext.show();
  104.     }
  106. }
  108. /**
  109.  * 用来存储迪杰斯塔拉算法算法中所使用的的几个数组
  110.  * @author Administrator
  111.  *
  112.  */
  113. class Vetext{
  114.     int[] alreadArr;
  115.     int[] dis;
  116.     int[] prePoint;
  118.     // 构造器
  119.     public Vetext(int len, int index) {
  120.         alreadArr = new int[len];
  121.         dis = new int[len];
  122.         prePoint = new int[len];
  123.         // 使用-1表示没有距离
  124.         Arrays.fill(dis, -1);
  125.         dis[index] = 0;        // 初始点的距离为0
  126.     }
  128.     /**
  129.      * 展示数组
  130.      */
  131.     public void show() {
  132.         System.out.println("节点是已访问：");
  133.         System.out.println(Arrays.toString(alreadArr));
  135.         System.out.println("节点的距离：");
  136.         System.out.println(Arrays.toString(dis));
  138.         System.out.println("前置节点的位置：");
  139.         System.out.println(Arrays.toString(prePoint));
  140.     }
  142.     /**
  143.      * 判断节点i是否被访问过了
  144.      * @param index
  145.      * @return
  146.      */
  147.     public boolean already(int index) {
  148.         return alreadArr[index] == 1;
  149.     }
  151.     /**
  152.      * 判断距离是否有效
  153.      * @param index
  154.      * @return
  155.      */
  156.     public boolean isDis(int index) {
  157.         return dis[index] != -1;
  158.     }
  160. }

弗洛伊德(Floyd)算法

弗洛伊德算法计算图中各个顶点之间的最短路径。
迪杰斯塔拉算法是计算选中访问顶点到其他各个顶点之间的最短路径。
image-20210120153335865.png
弗洛伊德算法的分析：

  1. 设置顶点vi到vk的最短路径已知为Lik，顶点vk到vj的最短路径为已知的Lkj，顶点vi到vj的路径为Lij。则vi到vj的最短路径为min((Lik+Lkj), Lij)。vk的取值为图中的所有顶点，则可以获得vi到vj的所有最短路径。
  2. 设置顶点的前驱关系图与顶点之间的距离图。

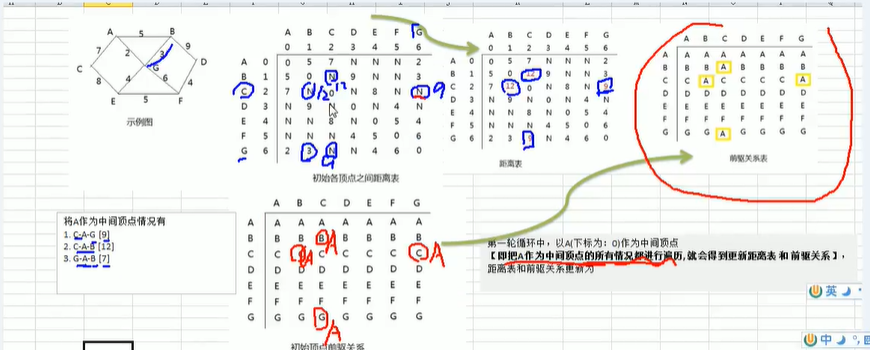
image-20210120162536272.png

代码的实现：

  1. public class FloydAlgorithm {
  2.     public static void main(String[] args) {
  3.         char[] point = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
  4.         int[][] matrix = new int[point.length][point.length];
  5.         final int N = -1;
  6.         matrix[0] = new int[]{0, 5, 7, N, N, N, 2};
  7.         matrix[1] = new int[]{5, 0, N, 9, N, N, 3};
  8.         matrix[2] = new int[]{7, N, 0, N, 8, N, N};
  9.         matrix[3] = new int[]{N, 9, N, 0, N, 4, N};
  10.         matrix[4] = new int[]{N, N, 8, N, 0, 5, 4};
  11.         matrix[5] = new int[]{N, N, N, 4, 5, 0, 6};
  12.         matrix[6] = new int[]{2, 3, N, N, 4, 6, 0};
  14.         FloydGraph floydGraph = new FloydGraph(point.length, matrix, point);
  15.         floydGraph.floyd();
  16.         floydGraph.show();
  17.     }
  19. }
  21. class FloydGraph{
  22.     char[] point;
  23.     int[][] dis;
  24.     int[][] pre;
  26.     public FloydGraph(int length, int[][] dis, char[] point) {
  27.         this.point = new char[length];
  28.         this.dis = new int[length][length];
  29.         this.pre = new int[length][length];
  31.         for(int i=0; i<length; i++) {
  32.             this.point[i] = point[i];
  33.         }
  35.         for(int i=0; i<length; i++) {
  36.             for(int j=0; j<length; j++) {
  37.                 this.dis[i][j] = dis[i][j];
  38.                 pre[i][j] = i;
  39.             }
  40.         }
  41.     }
  43.     /**
  44.      * 弗洛伊德算法，实现三层遍历算法
  45.      */
  46.     public void floyd() {
  47.         int len = 0;
  48.         // 第一次遍历 所有的节点作为中间节点，路径为i -> k -> j
  49.         for (int k = 0; k < point.length; k++) {
  50.             // 第二次遍历  节点作为开始节点
  51.             for (int i = 0; i < point.length; i++) {
  52.                 // 第三次遍历 节点作为结束节点
  53.                 for(int j = i+1; j<point.length; j++) {
  54.                     if(dis[i][k] == -1 || dis[k][j] == -1) continue;
  55.                     len = dis[i][k] + dis[k][j];
  56.                     if(dis[i][j] == -1 || len < dis[i][j]) {
  57.                         // 更新距离
  58.                         dis[i][j] = len;
  59.                         dis[j][i] = len;
  60.                         // 更新前缀
  61.                         pre[i][j] = pre[k][j];
  62.                         pre[j][i] = pre[k][j];
  63.                     }
  64.                 }
  65.             }
  66.         }
  67.     }
  69.     /**
  70.      * 打印dis与pre数组
  71.      */
  72.     public void show() {
  73.         System.out.println("打印dis位置数组：");
  74.         for(int i=0; i<point.length; i++) {
  75.             for (int j = 0; j < point.length; j++) {
  76.                 System.out.printf("%4d", dis[i][j]);
  77.             }
  78.             System.out.println();
  79.         }
  81.         System.out.println("打印pre前缀数组：");
  82.         for (int i = 0; i < point.length; i++) {
  83.             for (int j = 0; j < point.length; j++) {
  84.                 System.out.printf("%4d", pre[i][j]);
  85.             }
  86.             System.out.println();
  87.         }
  89.         System.out.println("打印节点之间的距离关系：");
  90.         for (int i = 0; i < point.length; i++) {
  91.             for (int j = 0; j < point.length; j++) {
  92.                 System.out.print("<" + point[i] + "," + point[j] + ">=" + dis[i][j] +"   ");
  93.             }
  94.             System.out.println();
  95.         }
  96.     }
  97. }

马踏棋盘算法（骑士周游算法）

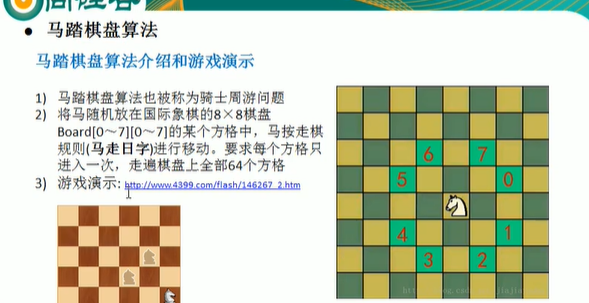
image-20210120165831900.png
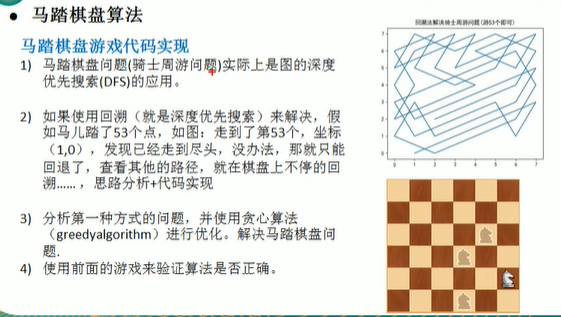
image-20210120170115405.png

骑士周游问题的解决步骤和思路：

  1. 创建棋盘chessboard，是一个二维数组
  2. 将当前位置设置为已经访问了，然后根据当前位置，计算马儿还能走哪些位置，并放入到一个集合中，最多有8个位置，每走1步，就使用step+1
  3. 遍历ArrayList中所存放的所有位置，看看哪个位置可以走通，如果能够走通，就继续，走不通就回溯。
  4. 判断马儿是否完成了任务，使用step和该走的步数进行比较，如果没有达到数量，则表示没有完成任务，将整个棋盘置0；

使用贪心算法的贪心策略，减少
代码的实现:

  1. import java.awt.Point;
  2. import java.util.ArrayList;
  3. import java.util.Arrays;
  4. import java.util.Comparator;
  5. import java.util.List;
  8. public class HorseChessBorad {
  9. //    private static int[][] chessborad;
  10.     private static int col;
  11.     private static int row;
  12.     private static boolean[] visited;
  13.     private static boolean finished;
  15.     // 骑士周游问题
  16.     public static void main(String[] args) {
  17.         System.out.println("骑士周游算法开始。。。");
  18.         row = 8;
  19.         col = 8;
  20.         visited = new boolean[row * col];
  21.         finished = false;
  22.         int[][] chessborad = new int[row][col];
  23.         long start = System.currentTimeMillis();
  24.         ChessBoradRun(chessborad, 0, 0, 1);
  25.         long end = System.currentTimeMillis();
  27.         System.out.println("花费的时间为：" + (end - start) + "毫秒");
  29.         for(int[] rows: chessborad) {
  30.             System.out.println(Arrays.toString(rows));
  31.         }
  33.     }
  36.     /**
  37.      * 用来解决骑士周游问题的最主要的方法
  38.      * @param board 表示棋盘的位置
  39.      * @param i    表示当前为第i行
  40.      * @param j    表示当前为第j列
  41.      * @param step    表示当前步数
  42.      */
  43.     public static void ChessBoradRun(int[][] board, int i, int j, int step) {
  44.         board[i][j] = step;
  45.         visited[i * col + j] = true;
  46.         List<Point> points = getNext(new Point(j, i));
  47.         pointSort(points);
  48.         while(!points.isEmpty()) {
  49.             Point p = points.remove(0);
  50.             if(!visited[p.y * col + p.x]) {
  51.                 ChessBoradRun(board, p.y, p.x, step+1);
  52.             }
  53.         }
  54.         // 如果没有step没有遍历完成所有的网格，则需要进行回退
  55.         if(step < col * row && !finished) {
  56.             board[i][j] = 0;
  57.             visited[i * col + j] = false;
  58.         }else {
  59.             finished = true;
  60.         }
  62.     }
  64.     /**
  65.      * 根据获得下一步中的点的下一步中最少点数进行非递减排序
  66.      * @param list
  67.      */
  68.     public static void pointSort(List<Point> list) {
  69.         list.sort(new Comparator<Point>() {            
  70.             @Override
  71.             public int compare(Point o1, Point o2) {
  72.                 return getNext(o1).size() - getNext(o2).size();
  73.             }
  74.         });
  75.     }
  78.     /**
  79.      * 获取下一步将要走的位置
  80.      * @param point
  81.      * @return
  82.      */
  83.     public static List<Point> getNext(Point point){
  84.         int[] steps = {-2, -1, 2, 1, -2, 1, 2, -1, -2};
  85.         Point p = new Point();
  86.         List<Point> result = new ArrayList<>();
  87.         for (int i = 0; i < steps.length-1; i++) {
  88.             p.x  = point.x + steps[i];
  89.             p.y = point.y + steps[i+1];
  90.             if(p.x < 0 || p.y < 0 || p.x >= col || p.y >= row) {
  91.                 continue;
  92.             }
  93.             result.add(new Point(p));
  94.         }
  95.         return result;
  96.     }
  97. }