引言:
(1)基于二叉树的链式存储结构讨论二叉树的如下主要操作:
先序遍历操作
中序遍历操作
后序遍历操作
(2)关于如何构建二叉树的问题,将在本部分的相关实验教学中,讨论完全二叉树的构建方法。
(3)重点知识:
先序遍历操作(递归算法)
中序遍历操作(递归算法)
后序遍历操作(递归算法)
中序遍历的非递归算法(利用堆栈)
层次遍历算法(非递归、利用队列)
(4)难点:
理解递归遍历算法
利用堆栈实现中序遍历的非递归算法
利用队列实现层次遍历的非递归算法
1. 先序遍历
对先序遍历、中序遍历及后序遍历的基本理解
各种次序的遍历方法都是以二叉树的根节点作为参照来定义的。
所谓先序遍历就是先遍历二叉树的根节点 ;
所谓中序遍历就是在中间遍历根节点;
所谓后序遍历就是在最后遍历根节点。
(1)先序遍历的基本方法

(2)先序遍历的过程分析
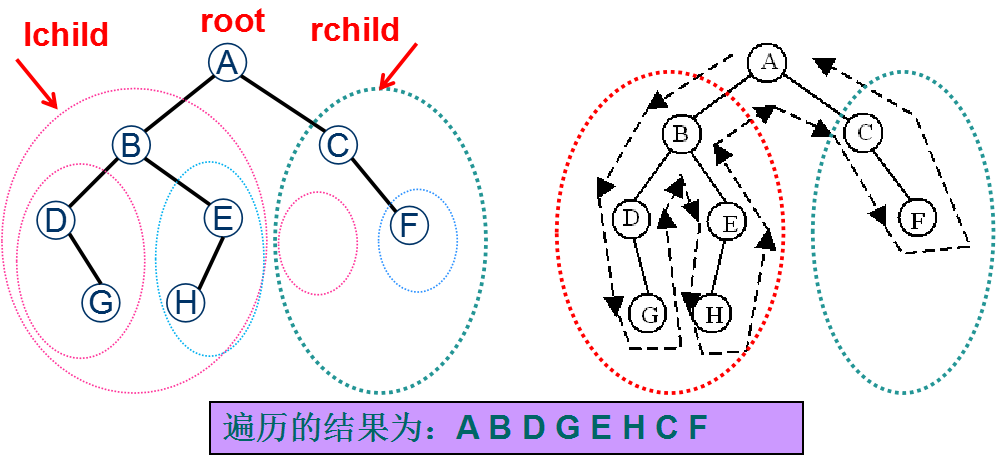
上述二叉树的先序遍历过程讲解:
(1)找到整个二叉树的根结点,遍历根结点(访问根节点)。
(2)先序遍历根节点的左子树(递归);所谓递归,就是将该左子树看成一个独立的二叉树,对其进行
先序遍历。
(3)先序遍历根节点的右子树(递归);所谓递归,就是将该右子树看成一个独立的二叉树,对其进行
先序遍历。
直到二叉树的所有结点都被遍历,形成先序遍历序列。
对如上图所示二叉树的遍历过程:<br /> (1)遍历整个二叉树的根结点,得到结点: A<br /> (2)先序遍历根节点A的左子树,得到结点序列:BDGEH<br /> (3)先序遍历根结点A的右子树,得到结点序列:CF<br /> 所以,最后得到整个二叉树的先序遍历序列: A BDGEH CF<br /> (根结点) (A的左子树序列) (A的右子树序列)<br />**(3)先序遍历算法实现**<br /> 
2. 中序遍历
(1)中序遍历的基本方法

(2)中序遍历的过程分析
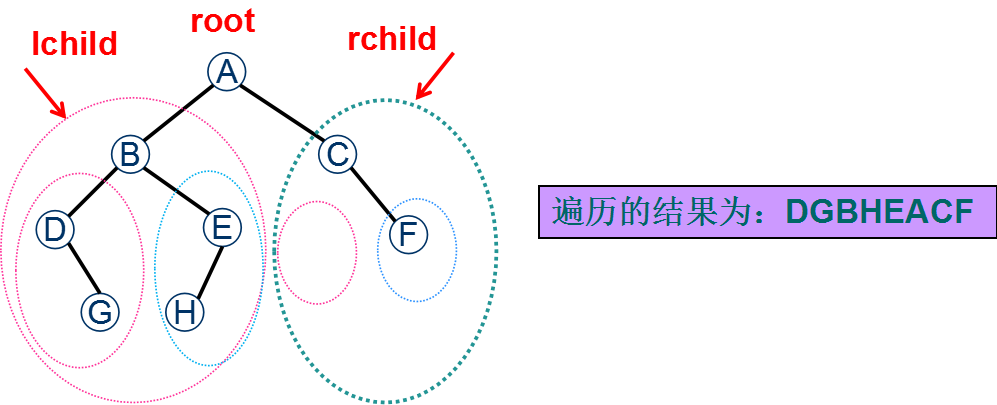
上述二叉树的中序遍历过程讲解:
(1)中序遍历根节点的左子树(递归);
(2)遍历根结点(访问根节点);
(3)中序遍历根节点的右子树(递归);
直到二叉树的所有结点都被遍历,形成先序遍历序列。
对如上图所示二叉树的遍历过程:<br /> (1)中序遍历二叉树根结点的左子树,得到结点序列:DGBHE<br /> (2)遍历根结点,得到结点 A<br /> (3)中序遍历根结点的右子树,得到结点序列:CF<br /> 所以,最后得到整个二叉树的先序遍历序列: DGBHE A CF<br /> (A的左子树序列) (根结点A) (A的右子树序列)<br />**(3)中序遍历算法实现**<br /> <br />**3. 后序遍历**<br />**(1)后序遍历的基本方法**<br /> <br />**(2)后序遍历的过程分析**<br /> 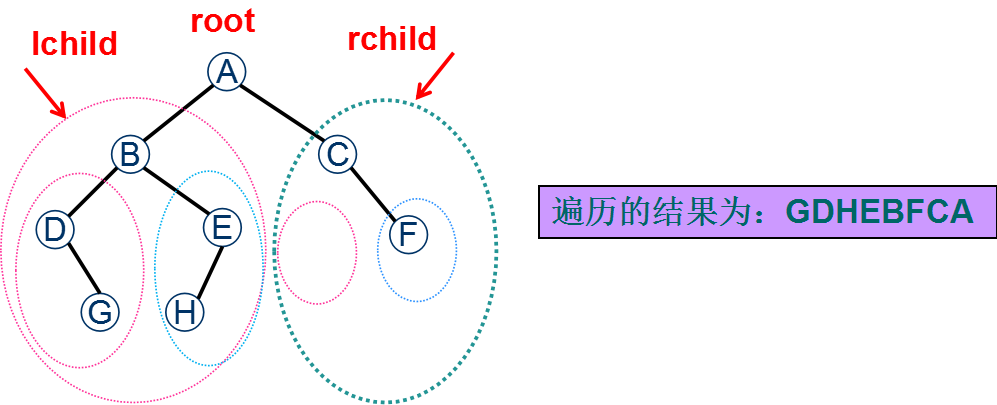<br /> 上述二叉树的后序遍历过程讲解:<br /> (1)后序遍历根节点的左子树(递归);<br /> (2)后序遍历根节点的右子树(递归);<br /> (3)遍历根结点(访问根节点);<br /> 直到二叉树的所有结点都被遍历,形成先序遍历序列。
对如上图所示二叉树的遍历过程:<br /> (1)后序遍历二叉树根结点的左子树,得到结点序列:GDHEB<br /> (2)后序遍历根结点的右子树,得到结点序列:FC<br /> (3)遍历根结点,得到结点 A<br /> 所以,最后得到整个二叉树的先序遍历序列: GDHEB FC A<br /> (A的左子树序列) (A的右子树序列) (根结点A) <br />**(3)后序遍历算法实现**<br /> 

