本章节包含：

1. 参考介绍
2. 文章解读

1. 参考介绍

Intro: Stanford University & The University of Adelaide
URL: GIoU论文 , GIoU解读
Github: darknet with GIoU
Unofficial Pytorch Implementation of GIoU

2. 文章解读

2.1 整体介绍

IoU 是目标检测benchmarks中使用最广的评估指标，然而，优化回归bounding box参数的距离损失（e.g. 范数 ）并不等价于最大化IoU指标（i.e. 距离损失函数与IoU相关性不大）。对于轴对齐的2D bbox，IoU 可直接用作回归损失，但是 IoU 无法优化无重叠的bbox，因此本文提出一种泛化版的IoU，名为 GIoU。结合 GIoU 和 SOTA目标检测框架，Faster R-CNN、Mask R-CNN 和 YOLOv3，在流行的目标检测benchmarks例如 PASCAL VOC 和 MS COCO中，分别使用标准 IoU 和 GIoU 损失，性能都得到了不同程度的提升。

2.2 方法介绍

Motivation

边界框回归（bbox regression）是2D/3D 视觉任务中一个最基础的模块，不管是目标检测，目标跟踪，还是实例分割，都依赖于对bbox进行回归，以获得准确的定位效果。目前基于深度学习的方法想获得更好的检测性能，要么是用更好的backbone，要么是设计更好的策略提取更好的feature, 然而却忽视了bbox regression中 loss这个可以提升的点。

“IoU , also known as Jaccard index, is the most commonly used metric for comparing the similarity between two arbitrary shapes.”

IoU formula：

IoU 本质是 Jaccard 系数，通常被用来计算两个任意形状图形的相似程度, 也是目标检测中一个重要的概念，在anchor-based的方法中，其作用不仅用来判定正样本和负样本，还可以用来评价输出框（predicted BBox）和ground-truth BBox的差距，或者说 predicted BBox 的准确性。

“IoU encodes the shape properties of the objects under comparison, e.g. the widths, heights and locations of two bounding boxes, into the region property and then calculates a normalized measure that focuses on their areas (or volumes).”

IoU将形状信息进行了编码，然后又进行了归一化，这使得 IoU 对尺度不敏感（scale invariant）这个特质使得IoU在目标检测、实例分割和目标跟踪都依赖于它。（ps 原始的 loss都对尺寸敏感）

在回归任务中，判断predicted BBox和gt的差距最直接的指标就是IoU，但目前目标检测器所采用的loss却不适合（范数），如图1所示，在loss相同的情况下，回归的效果却大不相同，即loss没有体现出回归的效果，而IoU却可以根据不同的情况得到不同的数值，能最直接反应回归效果。说明回归中的loss函数与IoU相关性不大。

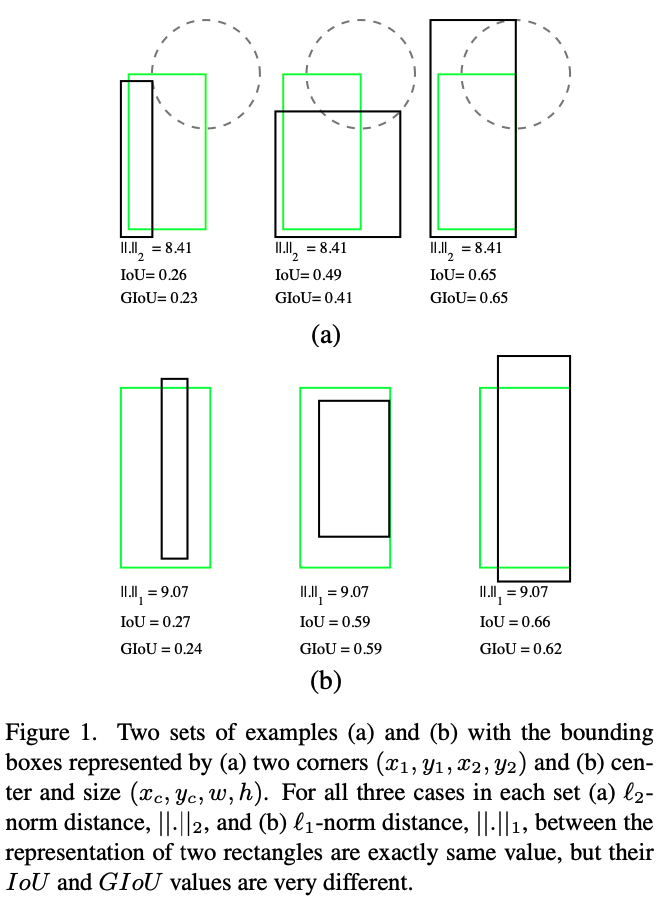
图1 相同loss，不同IoU的情况
**

Method

“It is therefore preferable to use IoU as the objective function for 2D object detection tasks. Given the choice between optimizing a metric itself vs. a surrogate loss function, the optimal choice is the metric itself. “

IoU作为一个评价检测定位精度度量，显然将其作为损失函数进行优化是最好的的选择。

IoU既然是最好的选择，但为什么之前的目标检测器都不用其做为loss进行优化呢，是因为IoU存在两大缺陷：

• “if two objects do not overlap, the IoU value will be zero. In this case of non-overlapping objects, if IoU is used as a loss, its gradient will be zero and cannot be optimized. “ 如果两个框没有重叠，那么IoU就会等于0，loss 等于0, 其梯度也等于0，因此会影响网络的训练。
• “if two objects do not overlap, the IoU value will not reflect how far the two shapes are from each other. “ 显然当两个框没有重叠的时候，IoU等于0,没法判断这两个框的距离远近。

为了解决IoU的上述两个问题，作者提出了GIoU，其算法如下：

图2 GIoU 算法及公式
GIoU的定义很简单，就是先计算两个框的最小闭包区域面积，再计算IoU，再计算闭包区域中不属于两个框的区域占闭包区域的比重，最后用IoU减去这个比重得到GIoU。论文中作者认为 GIoU 具有以下几个性质:

• 与 IoU 类似，GIoU满足距离度量的性质（非负性、对称性和满足三角不等式）计算损失函数时可用 Loss GIoU=1−GIoU 来计算；
• 同样，GIoU 也对物体的大小不敏感；
• 根据上面的公式可以看出，GIoU 总是会小于或等于 IoU（下界）。 另外对于 IoU 而言，其值域为 [0,1], 而 GIoU 的值域为 [−1,1]。在两个形状完全重合时，有 GIoU = IoU = 1，当两个形状没有重叠部分时，IoU 为 0, 减数为 1（当两个框相距无限远）, 所以此时的 GIoU 为 - 1；
• 由于 GIoU 引入了包含 A,B 两个形状的 C， 所以当 A,B 不重合时，依然可以进行优化。GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度。

GIoU和IoU作为loss的算法如下图3所示:

图3 和 算法
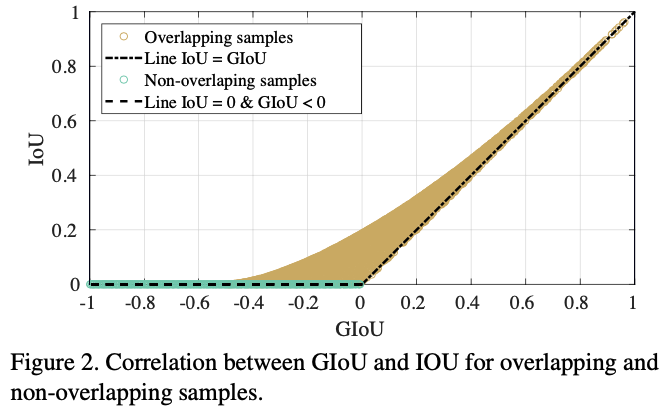
根据指标检测性能时，以指标本身作为损失来优化显然是最佳选择，但是在bbox非重叠场景下，IoU=0，其梯度也为0，影响训练质量和收敛速度，相反，GIoU 则一直能有效梯度指导如何优化模型。另外，根据GIoU性质3，GIoU 与 IoU 强相关，在 IoU 较大时，这种强相关更加显著。下图4 定性的分析了这种相关性，并且在IoU≤0.2和GIoU≤0.2 时，GIoU明显具有更陡的梯度，更加容易进行优化。

图4 GIoU 与 IoU 的相关性

Innovation

在IoU的基础上进行了改进，即GIoU。

“Therefore, optimizing GIoU as loss, Loss GIoU can be a better choice compared to Loss IoU, no matter which IoU-based performance measure is ultimately used .”

作者认为GIoU的指标比**任何形式IoU的指标都好**。
GIoU 解决了 IoU 的两个重大的缺陷。 作者在三种检测器上进行了比较**，**使用GIoU之后均有所提升，YOLOv3 在Pascal VOC2007上能提升1-3个AP。