:::warning
本文为逻辑结构分析展述，从数据输入，正向传播，输出处理，反向传播，完成一次训练迭代为主要逻辑
:::
一.正向传播流程
:::info
下面进行分块解释
:::
数据输入的预处理
1.标准化
2.参数初始化
W1，W2等都是参数组成的矩阵
一般采用随机策略来进行参数初始化
:::info
注意：为了减少过拟合情况，不能让初始参数的值差距过大，所以采用 w=0.01*np.random.radn(D,H) 让初始参数差距减小
:::
激活函数
在数据处理中，激活函数用于把经过上一层参数矩阵乘法线性变换后的数据进行一次非线性变换，再进入下一层参数矩阵乘法线性变换。
深层作用：如果不用激活函数（其实相当于激活函数是f(x) = x），在这种情况下你每一层节点的输入都是上层输出的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了，那么网络的逼近能力就相当有限。正因为上面的原因，我们决定引入非线性函数作为激励函数，这样深层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数）。
对激活函数深层作用的举例和理解|常见的激活函数
(23条消息) 激活函数（Activation Function）意念回复的博客-CSDN博客激活函数是什么.pdf
:::warning
以上正向传播过程可以当做得分函数f(x,W)的一部分(即W)，经过+b的微调后得到最终的输出层数据
:::
:::danger
请注意，输出层数据实际上是经过一系列参数矩阵线性变换和非线性激活函数处理过的，包含输入层数据和多层参数，激活函数的表达式（该表达式也可被计算出数值进行比较，且可用于计算损失函数和代价函数）
:::
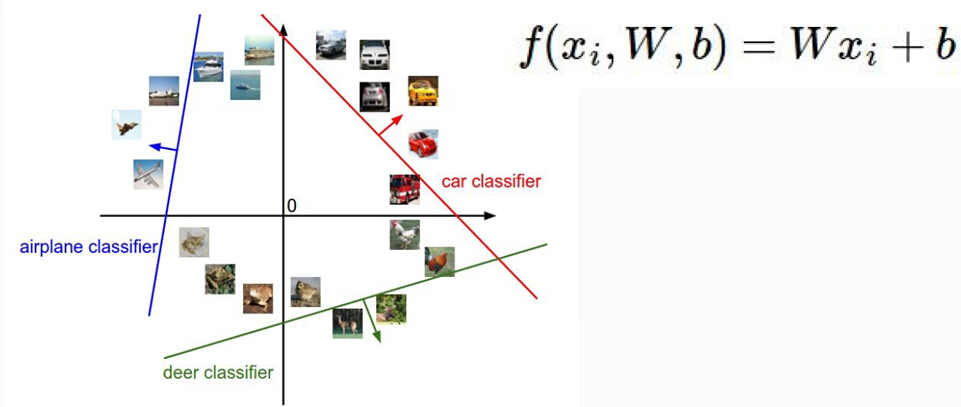
二.对得分函数输出结果的处理
先展示处理过程中涉及的函数
(23条消息) 机器学习中的代价函数、损失函数、风险函数、目标函数长路漫漫2021的博客-CSDN博客风险函数和代价函数.pdf
损失函数
对单个样本正向传播（得分函数）输出结果的损失值（data-loss）计算
代价函数
softmax分类器
该分类器可将得分函数输出值转化为正确概率
(23条消息) 一分钟理解softmax函数（超简单）_-永不妥协-的博客-CSDN博客_softmax函数.pdf
在不同的任务中得分函数的结果有不同的处理方法
在回归任务中，由得分值计算损失
在分类任务中，由概率值计算损失
计算损失后通过反向传播对W进行矫正修改，以完成一次训练
三.反向传播流程|BP算法详解
BP算法的一般流程
根据BP算法的基本思想,可以得到BP算法的一般过程:
1) 正向传播FP(求损失).在这个过程中,我们根据输入的样本,给定的初始化权重值W和偏置项的值b, 计算最终输出值以及输出值与实际值之间的损失值.如果损失值不在给定的范围内则进行反向传播的过程; 否则停止W,b的更新.
2) 反向传播BP(回传误差).将输出以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元，从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。
由于BP算法是通过传递误差值δ进行更新求解权重值W和偏置项的值b, 所以BP算法也常常被叫做δ算法.
下面我们将以三层感知器结构为例,来说明BP算法的一般计算方法(假设个隐层和输出层的激活函数为f).
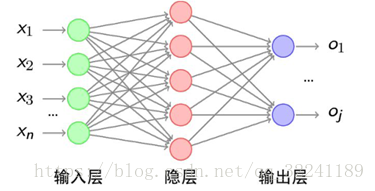
图2 三层感知器结构
BP算法网络结构的示意图如图3所示.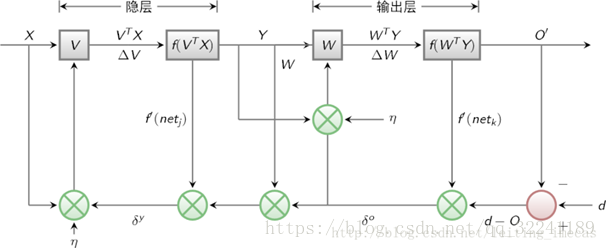 
图3 BP算法网络结构
BP算法的各层误差计算
各部分输入输出如图3所示, 下面进行各层误差计算.<br /> 1) 输出层的误差(平方和误差,前面的1/2是为了后面的计算方便)<br />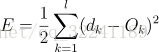<br /> (1)<br /> 2) 展开至隐层的误差(,是前面的WY的输出值,带入可以得到下面的式子)<br /><br /> (2)<br /> 3) 输入层误差(和前面一样,将VX带入f(netj))<br />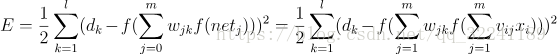<br /> (3)<br /> 观察上式, 我们很容易看出只有(3)式和输入x有关.E有了,那么就很简单可以看出可以使用常用的随机梯度下降法(SGD)求解.也就是求解式子中的W和V,使得误差E最小.
BP算法的示例
已知如图4所示的网络结构.
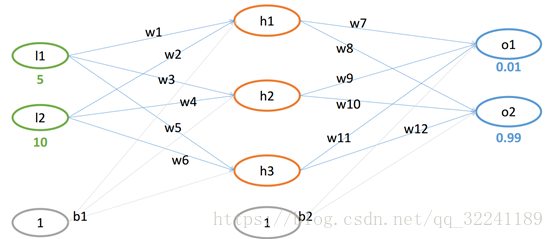
图4 网络结构图
设初始权重值w和偏置项b为:
w=(0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.65)
b = (0.35,0.65)-->这里为了便于计算,假设从输入层到隐层之间, 隐层到输出层之间的偏置项b恒定.
1) FP计算过程
① 从输入层到隐层(其实这里的b可以看成一个特征)
h1 = w1*l1 +w2*l2 +b1*1 = 0.1*5+0.15*10+0.35*1 = 2.35
h2 = w3*l1 +w4*l2 +b1*1 = 0.2*5+0.25*10+0.35*1 = 3.85
h3 = w5*l1 +w6*l2 +b1*1 = 0.3*5+0.35*10+0.35*1 = 5.35
则各个回归值经过激活函数变换后的值为:<br />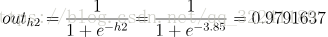 
② 隐层到输出层
neto1 = outh1*w7 +outh2*w9 +outh3*w11+ b2*1= 2.35*0.4 + 3.85*0.5 +5.35 *0.6+0.65 = 2.10192
neto2 = outh1*w8 +outh2*w10 +outh3*w12 +b2*1= 2.35*0.45 + 3.85*0.55 +5.35 *0.65 +0.65= 2.24629
则经过激活函数变换得到:
outo1 = 0.89109 (真实值0.01) , outo2 = 0.90433 (真实值0.99)
此时的平方和误差为:
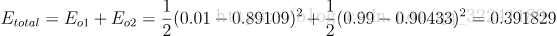 <br /> 与真实值不符,需要进行BP反馈计算.<br /> 2) BP计算过程
这里的BP计算我们分为两个部分. ①隐层到输出层的参数W的更新 ②从输入层到隐层的参数W的更新.
**在这里,我们主要讲述第一部分隐层到输出层的参数W的更新.
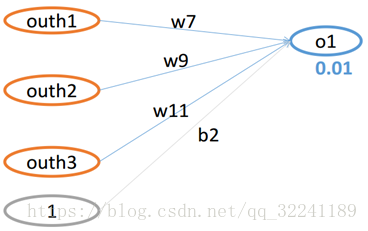
图5 从隐层到输出层的网络结构图
如图5所示为从隐层到输出层的网络结构图.
首先,运用梯度下降法求解W7的值.
目标函数: ,由于此时求解W7,所以只与有关,则此时的损失函数为: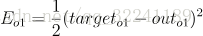
可以看出, 为凸函数(开口向上), 有最小值且最小值在导数为0的点上.
又有 neto1 = outh1*w7 +outh2*w9 +outh3*w11+ b2*1, outo1 = f(o1)
则对W7求偏导数得到:<br /><br /> (4)
又有W的更新公式为:
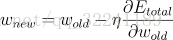<br />(5)<br /> 这样将上式带入W的更新公式(5)就可以求得更新后的W值.
最后,得到了W7的更新值为:
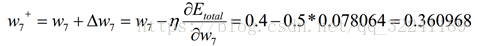
同理可以求得W9,W11,b2的更新值,这里就不在一一叙述了.
***对于从输入层到隐层的参数W的更新,其实和从隐层到输出层的几乎一样,唯一不同的就是链式求导过程中的Etotal和outo1,outo2都有关系.这里就不展开解释了.
反向传播矫正参数的原理
(23条消息) 神经网络BP反向传播算法原理和详细推导流程Z_y_forever的博客-CSDN博客神经网络反向传播算法推导.pdf
我讲两句： 1.反向传播是通过前向传播的输出值经损失函数计算出的损失值（data-loss）和前向传播的输出表达式经过梯度下降算法对前面每一层进行依次反向求偏导并修改相应参数（程度依据梯度下降步长）的过程 2.
四.对于过拟合的解决方法
drop-out（七伤拳）
在训练每一个样本的过程中对每一层神经元进行随机封杀功能，这样做可以有效避免过拟合，但也可能欠拟合，注意：在测试过程中所有神经元都要参与。
损失函数正则化
正则化是通过限制损失函数过高次项的参数大小来避免模型过拟合
(23条消息) 知识卡片 损失函数的正则化_「已注销」的博客-CSDN博客.pdf
引用出处
原文链接：https://blog.csdn.net/qq_32241189/article/details/80305566
若有收获，就点个赞吧
0 人点赞
