排序-1亿数据，1M内存，求TOP10，看看堆排序如何实现

什么是堆

堆是计算机程序中一种数据结构，堆是一种特殊的树（完全二叉树），完全二叉树是说除了最后一层，其它层的节点必须是满的(也就是说左右子树的高度差不能超过一)，最后一层的节点必须靠左排列。堆中每个节点的值都必须大于等于或者小于左右子节点的值。只有符合这两点的数据结构才是堆。
总结符合如下两个要求的才是堆

1. 是一个完全二叉树
2. 每个节点的值都必须大于等于或者小于左右子节点的值

将父节点值大于等于左右子节点的值的堆叫做大顶堆
将父节点值小于等于左右子节点的值的堆叫做小顶堆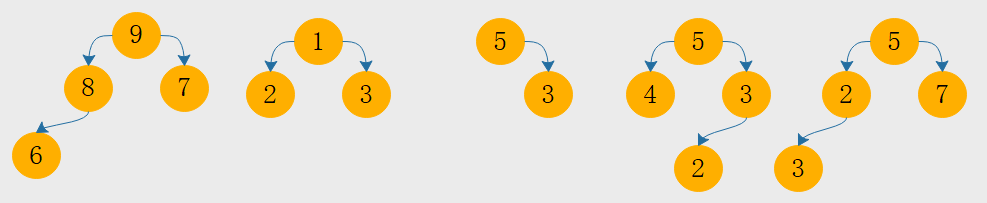

我们看上面的图分析得知：图一是一个大顶堆，图二是一个小顶堆，图三不是一个完全二叉树，因为最后一层的节点没有靠左排列，图四是一个完全二叉树，但5这个节点大于它的左节点小于它的右节点，不符合堆的要求。

什么是堆排序

堆排序是指利用堆这种数据结构设计的一种排序算法，在说堆排序之前，我们首先看看如何用数组表述一个堆呢？看上面的第一幅图（9，8，7，6），顶节点是9，它的左节点是8，右节点是7，在数组中9对应的下标是0，依次8对应1，7对应2，6对应3。

我们看图能不能找到数组下标和堆中左右节点的一个规律，求9的左节点8等于0+1，右节点7等于0+2，8的左节点6等于1 2 +1，我们给上面的0+1,0+2的0都乘以2，可以得到一个公式，一个节点的左节点等于这个节点的下标乘以二加一，右节点等于这个节点的下标乘以二加二。
总结，在一个数组中，下标从零开始：
**父节点的左儿子 = 父节点的下标 2 + 1
父节点的右儿子 = 父节点的下标 2 + 2*
那么我们如何对一个数组排序呢，比如数组[2,5,1,8,0] ？堆排序的过程分为两步，第一步建堆，第二步堆化（也就是调整堆），我们通过代码实践一下堆排序

//大顶堆排序
func BigHeapSort (array []int) {
    //为什么i=初始值是 len(array) /2 -1, 
    //因为这样求出来的i总是这个树中最后一层末尾节点的父节点，
    //从这个节点开始创建堆，不断调整节点，使得满足堆数据结构的要求
    for i:=len(array) / 2 -1; i>=0; i--{
        createHeap(array,i)
    }
    //调整堆
    for length:=len(array)-1; length>=0; length--{
        //将堆顶最大元素放入末尾
        array[0],array[length] = array[length],array[0]
        //重新调整剩下数组中元素，依次循环，最后数组的顺序就是从小到大
        adjustHeap(array,0,length-1)
    }
}
func createHeap(array []int, index int) {
    length := len(array)-1
    left := index * 2 +1
    for left < length {
        //求出左节点，右节点最大的那个几点
        right := left+1
        max := -1
        if right > length {
            max = left
        }else if array[left] > array[right]{
            max = left
        }else{
            max = right    
        }
        //如果最大节点小于父节点，则交换
        if array[index] < array[max]{
            array[index],array[max] = array[max],array[index]
        }
        //将index赋值为最大节点
        index = max
        //left是最大节点的左节点
        left = max * 2 +1
    }
}
//调整堆的过程跟创建堆的过程类似，其实可以合并成方法，
//为了大家理解，这里就不合并了
func adjustHeap(array []int, index ,length int){
    left := index * 2 +1
    for left < length {
        right := left+1
        max := -1
        if right > length {
            max = left
        }else if array[left] > array[right]{
            max = left
        }else{
            max = right    
        }
        if array[index] < array[max]{
            array[index],array[max] = array[max],array[index]
        }
        index = max
        left = max * 2 +1
    }
}

我们看下面的图来了解创建堆和调整对的整个过程，通过下图相信大家一定会理解的，如下图，第一行是创建堆的构成，后面两行是调整堆的过程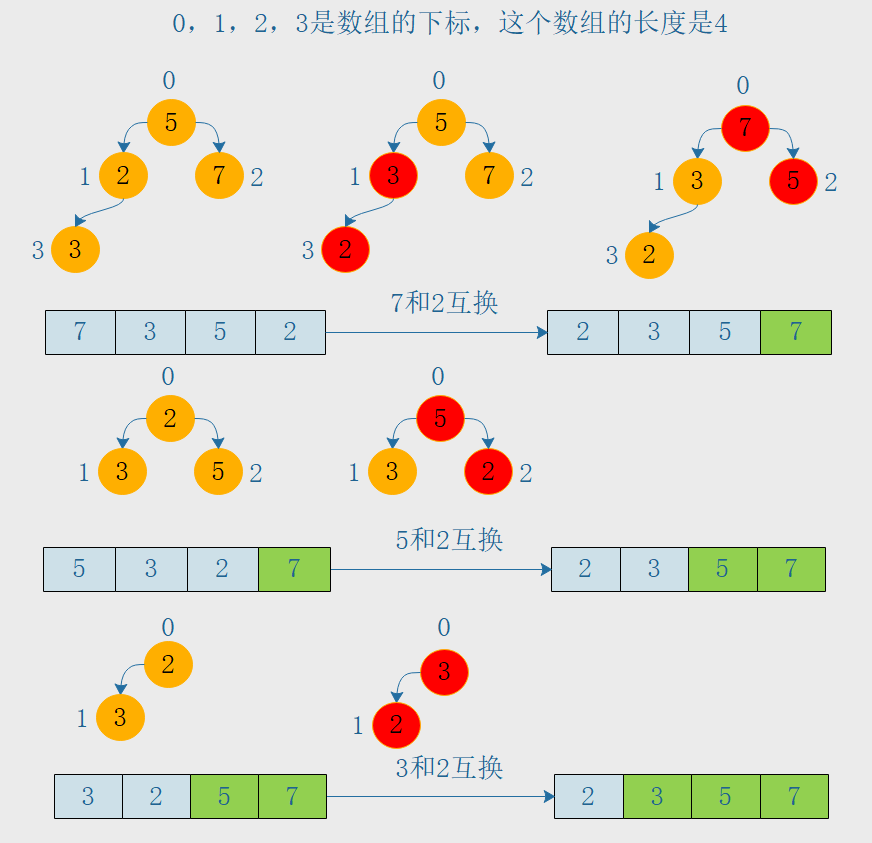

小顶堆的过程其实也是一样的，读者们好好思考一下，可以自己试着实现一下

实现标题中提出的问题

文章标题中提出1亿数据，1M内存，就TOP10，大顶堆的堆顶总是最大的，小顶堆的堆顶总是最小的，想一想此处我们应该用哪个呢？因为我们要求TOP10，我们一次性从文件中读取10个元素，将这10个元素构建成一个小顶堆，此时堆顶是最小元素，然后我们依次从文件中读取剩余的元素，每次读取一个，和堆顶元素比较，如果比堆顶的元素小，就直接舍弃，读取下一个（堆顶已经最小了，比堆顶还小，那肯定不是TOP10）,如果比堆顶元素大，将堆顶元素替换成当前元素，此时堆顶元素就不是最小了，所以这时重新调整堆，使得堆顶的元素是这个10个元素中最小的，然后进行下一步，直到文件中所有数据都比较完成，这时整个堆就是TOP10，然后堆排序，依次输出这10个元素。

func HeapSortComputeTop10(fileAddress string) ([]int, error) {
   file, err := os.Open(fileAddress)
   if err != nil {
      return nil, err
   }
   reader := bufio.NewReader(file)
   data, _ := reader.ReadString('\n')
   array := strArrayConvertIntArray(data)
   //构造小顶堆
   array = CreateSmallHeap(array)
   //计算topN
   computeTopN(array,reader)
   // 调整堆,就是排序的过程，结过为从大到小
   for i := len(array) - 1; i >= 0; i-- {
      array[i], array[0] = array[0], array[i]
      AdjustSmallHeap(array, 0, i)
   }
   return array, nil
}
func computeTopN(array []int, reader *bufio.Reader) []int {
   for {
      data, _ := reader.ReadString('\n')
      //数据已处理到结尾
      if len(data) == 0 {
         break
      }
      temp := strArrayConvertIntArray(data)
      for _, v := range temp {
         //比小顶堆堆顶元素还小
         if v < array[0] {
            continue
         }
         //否则，替换堆顶元素，重新调整堆
         array[0] = v
         array = CreateSmallHeap(array)
      }
   }
   return array
}
//字符串数组转int数组
func strArrayConvertIntArray(s string) []int {
   str := strings.Split(s, ",")
   array := make([]int, len(str))
   for k, v := range str {
      temp, _ := strconv.Atoi(v)
      array[k] = temp
   }
   return array
}
func CreateSmallHeap(intArray []int) []int {
   length := len(intArray)
   //建堆,把最大的放到顶部
   for i := length/2 + 1; i >= 0; i-- {
      adjustSmallHeap(intArray, i, length)
   }
   return intArray
}
func AdjustSmallHeap(intArray []int, i, length int) {
   //左子节点
   childrenNode := i*2 + 1
   for childrenNode < length {
      // 从子节点中找较小的
      if childrenNode+1 < length && intArray[childrenNode] >                                intArray[childrenNode+1] {
         childrenNode++
      }
      // 如果父节点 < 两个子节点中最小的，则说明父节点最小
      if intArray[i] > intArray[childrenNode] {
         // 把父节点和最小子节点交换
         intArray[i], intArray[childrenNode] = intArray[childrenNode], intArray[i]
      }
      // 父节点变更
      i = childrenNode
      // 父节点的子节点
      childrenNode = i*2 + 1
   }
}

堆的特性和应用场景

根据上面我们的分析，堆的一些特性总结如下：

1. 堆分为大顶堆和小顶堆
2. 大顶堆的堆顶元素时最大的
3. 小顶堆的堆顶元素时最小的
4. 堆本质也是一棵树(完全二叉树)
5. 堆排序的时间复杂度是Nlog(N),空间复杂度是O(1)

基于堆的第二条和第三条特性，可以在实际场景中做很多有意义的事，如下举例：

1. 文章标题的问题，求topN，可以使用堆数据结构
2. 优先级队列，优先级最高或者最低的先出队列，Jdk的优先级队列就是用堆实现的
3. 合并有序的小文件（仔细想想这个过程）
4. 高性能定时器，假设有一批任务，线程每隔很小的一个时间(1ms))扫描任务，看看有没有需要执行的,这样效率很低下，可以把这批任务构建成一个小顶堆，这样线程只需要监控堆顶的任务。
5. 求中位数，当数据是在不断变化的时候，我们讲数据较大的一部分放入大顶堆，较小的一部分放入小顶堆，当有新的元素进来时，如果比大顶堆的堆顶元素大，则放入大顶堆，如果比小顶堆的堆顶元素小，则放入小顶堆，最终两个堆的元素个数可能差异比较大，这时做元素移动，直到两个堆的元素个数相差不大于1，此时，如果数据总个数是偶数，则堆尾部的元素就是中位数,如果是奇数，则元素个数较多的那个堆的堆尾元素就是中位数.

读者们可以好好思考一下上面的应用场景，可以看看源码，或者自己实践一下。

欢迎大家关注微信公众号：“golang那点事”，更多精彩期待你的到来