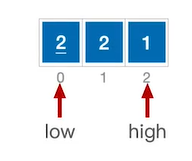
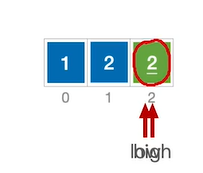
算法思想

寻找一个枢轴(基准，通常取首元素)，对整个表进行划分比枢轴小的在其左边，比枢轴大的在其右边，然后再以相同的方法处理左边和右边直至全部有序。
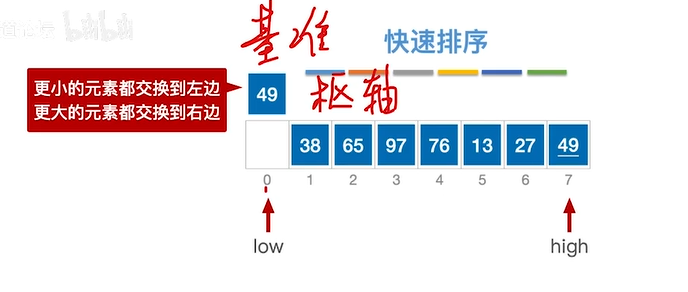
image.png

划分过程

image.png
使用low和high对所有元素进行扫描，右边≥基准元素，左边≤基准元素。同时要保证high>low。
因为取得基准为第一个元素(该位置假设为空)，所以第一趟先移动high指针。
此时high所指向的元素（49）≥49，因此不需要移动，执行high—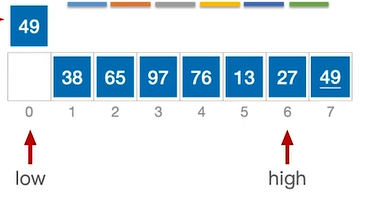
image.png
此时high所指向的元素（27）＜49，执行移动。将high位置的元素移动到low位置。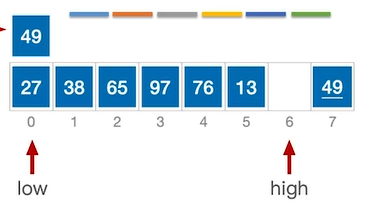
image.png
移动后high指针位置空出来了，那么需要移动low指针。此时low指针所指向元素(27)≤49，因此不需要移动，执行low++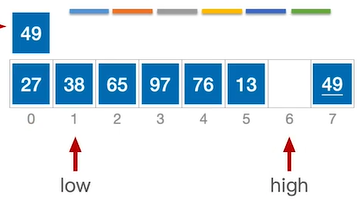
image.png
此时low指针所指向元素(38)≤49，因此不需要移动，执行low++。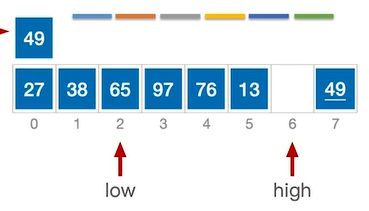
image.png
此时low指针所指向元素(65)≥49，执行移动，将low指向的元素移动至high指向的位置。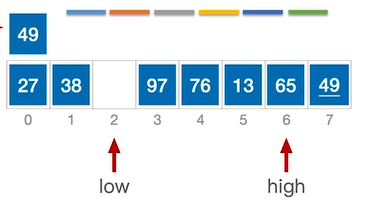
image.png
移动后low指针位置空出来了，那么需要移动high指针。此时high指针所指向元素(65)＞49，因此不需要移动，执行high—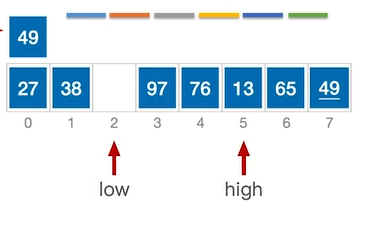
image.png
此时high所指向的元素（13）＜49，执行移动。将high位置的元素移动到low位置。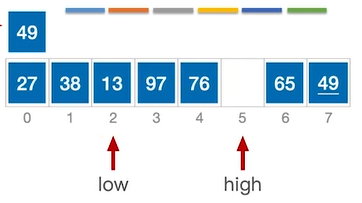
image.png
移动后high指针位置空出来了，那么需要移动low指针。此时low指针所指向元素(13)≤49，因此不需要移动，执行low++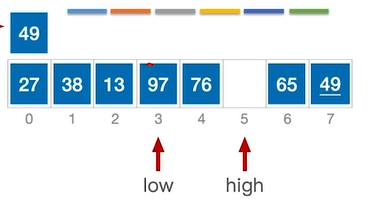
image.png
此时low指针所指向元素(97)＞49，执行移动，将low指向的元素移动至high指向的位置。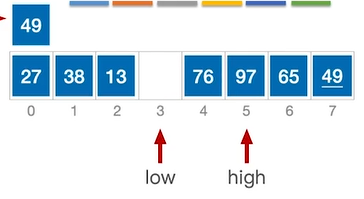
image.png
移动后low指针位置空出来了，那么需要移动high指针。此时high指针所指向元素(97)＞49，因此不需要移动，执行high—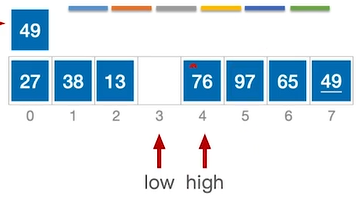
image.png
此时high所指向的元素（76）＞49，因此不需要移动，执行high—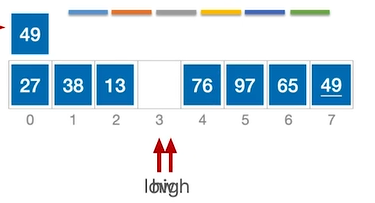
image.png
low和high指针相遇不满足high>low的条件划分结束。将所有待排序的元素都扫描了一边，所有比枢纽小的都在左边，比枢纽大的都在右边，那么此时low和high指向位置即为枢纽（49）的最终位置(一次划分确定了元素的最终位置),将枢纽的值填入此位置。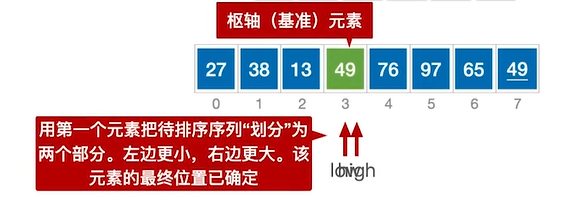
image.png
在接下来的排序中就不需要再管此时的枢轴（49）了，分别对其左边和右边的元素做相同的划分。

对左子表进行划分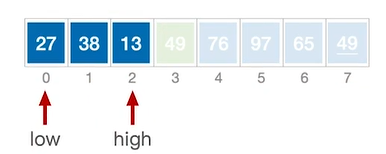
image.png
选中最前边的元素（27）作为基准元素。此时high所指向的元素（13）＜27，因此不需要移动，执行移动。将high位置的元素移动到low位置。
image.png
移动后high指针位置空出来了，那么需要移动low指针。此时low指针所指向元素(13)≤27，因此不需要移动，执行low++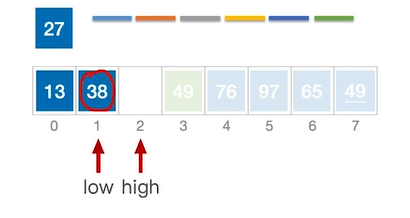
image.png
此时low指针所指向元素(38)＞27，执行移动，将low指向的元素移动至high指向的位置。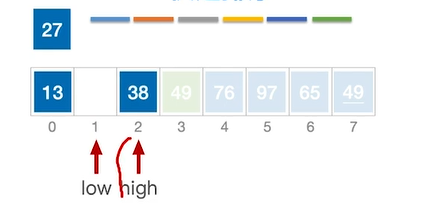
image.png
此时high所指向的元素（38）＞27，因此不需要移动，执行high—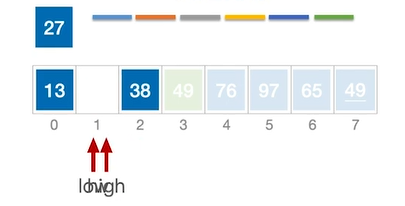
image.png
low和high指针相遇不满足high>low的条件划分结束。此时low和high指向位置即为枢纽（27）的最终位置。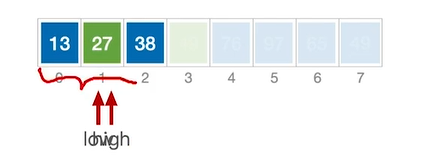
image.png
此时左右两个部分都只剩一个元素不需要再进行划分。

对右子表(索引为4-7)划分，划分过程同理。
最总结果如下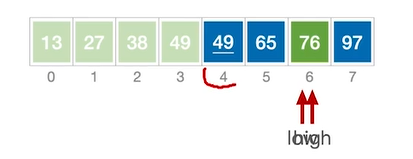
image.png
再分别对索引为4-5和7的两个子表进行划分
最终结果如下:
image.png
所有位置变得有序，快速排序完成。

代码实现

使用递归实现快速排序
image.png

算法效率分析

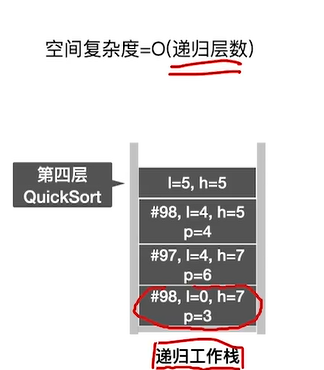
递归层数分析

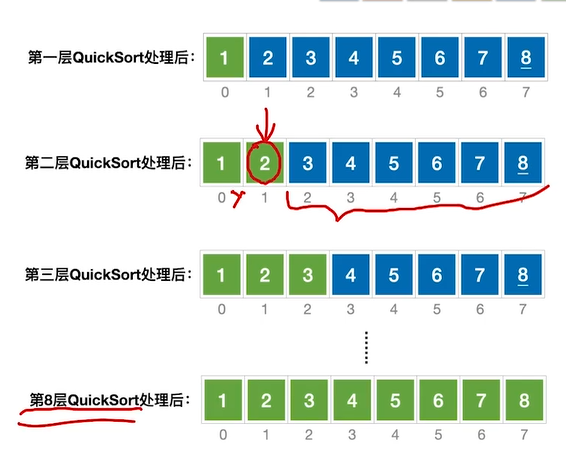
递归调用树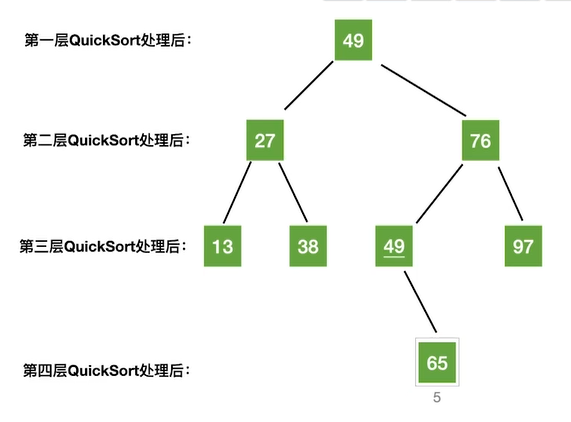
image.png
把n个元素组织成二叉树，二叉树的层数就是递归调用的层数。
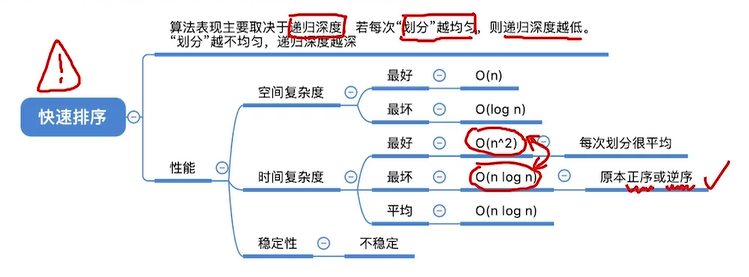
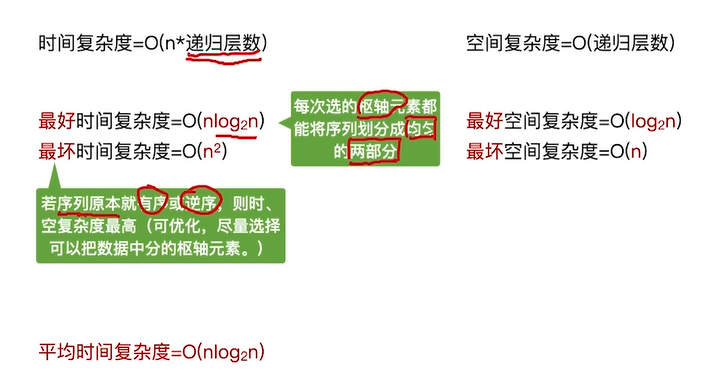
image.png

时间效率

image.png
image.png

空间效率

image.png
image.png

快速排序最坏情况

完全有序或者逆序，此时快速排序退化为冒泡排序。
image.png
image.png
image.png
image.png
image.png

效率总结

image.png
快速排序实在所有内部排序中平均性能最优的排序算法

稳定性

image.png
image.png
因此快速排序是不稳定的

总结

image.png