B（B-）树概念

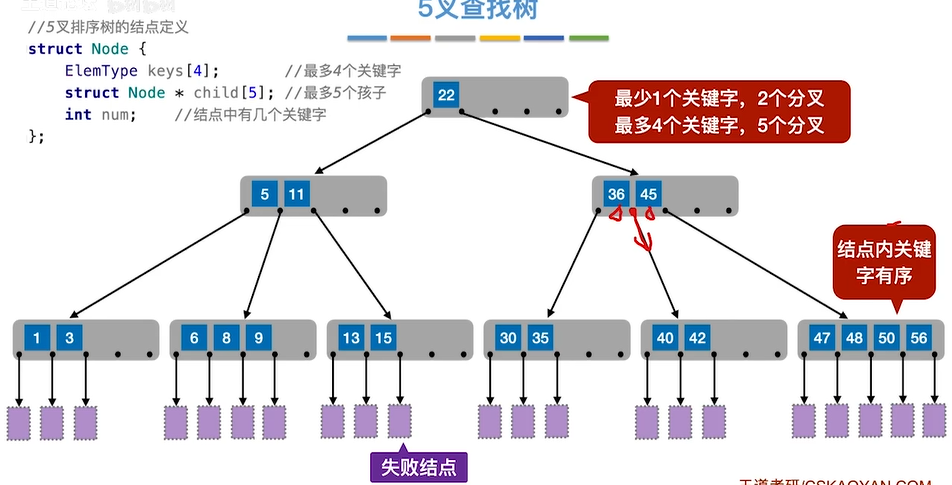
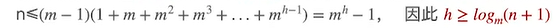五叉查找树：

如何保证m叉查找树的效率：

①每个结点的分支要求：

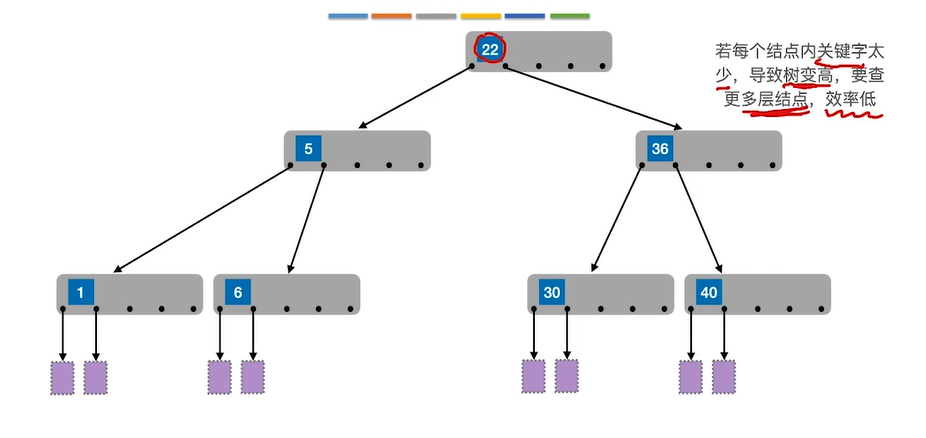
比如五叉查找树除了根节点每个结点至少有3（m/2向上取整）个分叉，则有两个关键字，查找效率可以得到保证

②子树平衡要求：

即不能有高度差

B树：

满足如何保证m叉查找树的效率两个条件的树成为B树，上面的五叉查找树就是一个B树

定义：

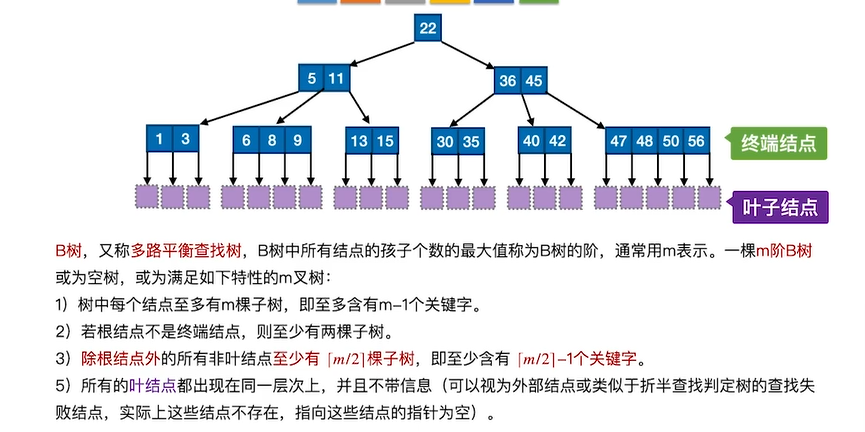
对于根节点，深度很深时一般只有两个分支。为啥看起来始终只有两个分支：请看这：https://blog.csdn.net/qq_34999565/article/details/112644993
注意叶子结点与平时树的叶子节点的区别。平时叶子结点就是终端结点，在B树中叶子节点时查找失败的结点（实际上不存在，为空指针），所有叶子结点都出现在同一层
对于条件2，可用用保证查找效率的要求2解释，即要求绝对平衡，左右子树高度要相同，那么最少就会有两颗子树

B树的核心特性：

B树的高度：

最小高度：

最大高度：

计算方法①


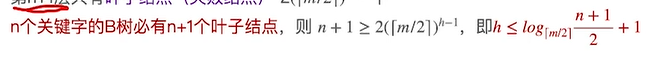
计算方法②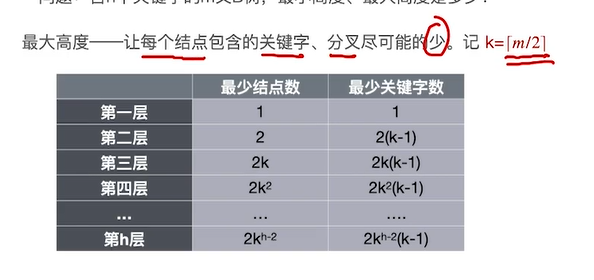


则对于含有n个关键字的m阶B树，高度范围如下：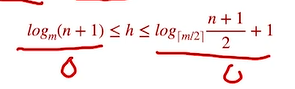

总结：