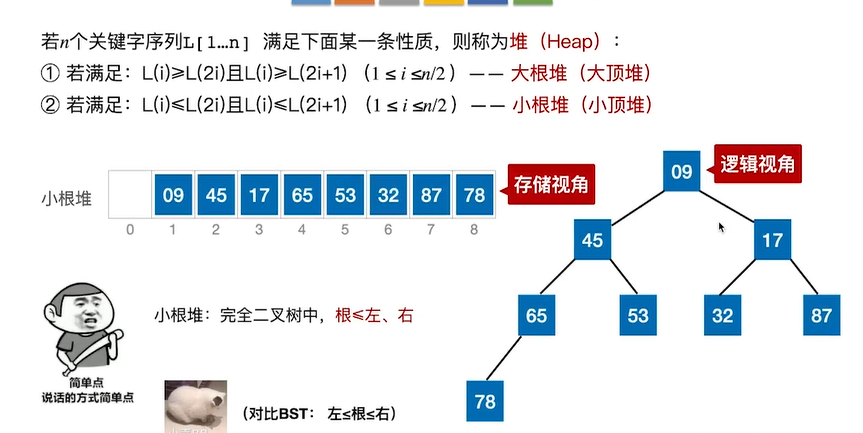
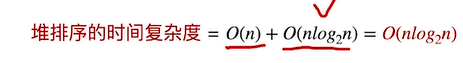堆的定义

若n个关键字序列L[1…n]满足下面某一条性质，则称为堆

大根堆

所有的子节点均小于父节点的完全二叉树为大根堆

小根堆

所有子节点均大于父节点的完全二叉树称为小根堆
image.png

建立大根堆

思路：检查所有非终端结点【编号i≤n/2向下取整】，判断其是否满足大根堆的条件，若不满足，则进行相应的调整。
从后往前依次处理非终端结点
处理思路如下
image.png

建立图示

①从最后一个非终端结点开始依次检查每个终端结点。下图右8个元素，则非终端结点为n/2向下取整，则为第四个元素9.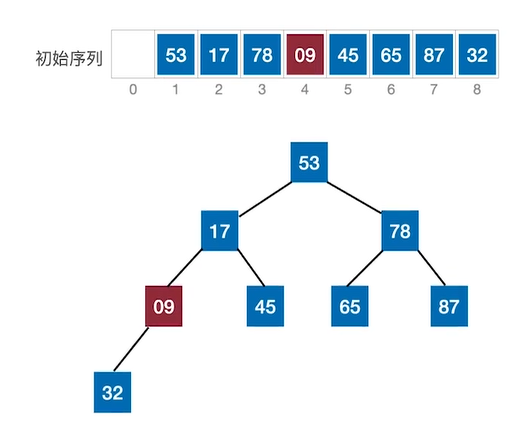
image.png
②检查索引为4(关键字9)为根节点的当前结点是否满足大根堆的要求。此时不满足，则需要调整，与其最大孩子互换。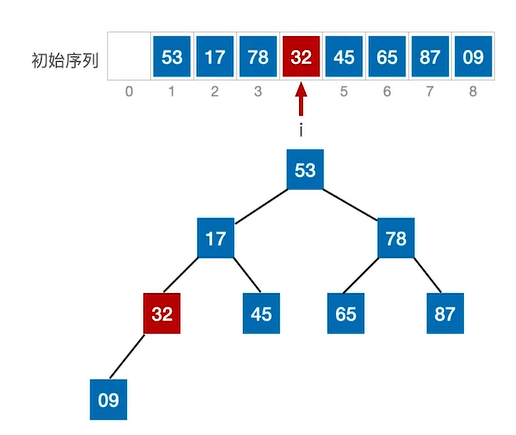
image.png
③检查下一个非终端阶段78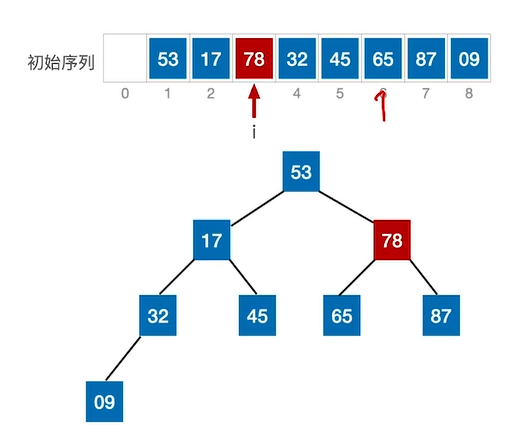
image.png
②检查索引为3(关键字78)为根节点的当前结点是否满足大根堆的要求。此时不满足，其右孩子比它大，则需要调整，与其最大孩子互换。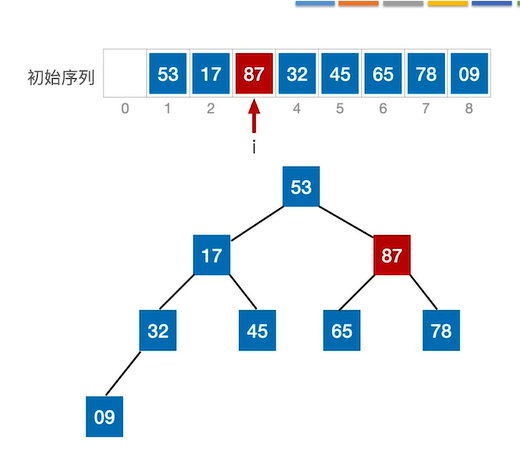
image.png
③检查索引为2(关键字17)为根节点的当前结点是否满足大根堆的要求。此时不满足，其左右孩子都比它大，则需要调整，与其最大孩子互换。
image.png
④检查索引为1(关键字53)为根节点的当前结点是否满足大根堆的要求。此时不满足，其右孩子比它大，则需要调整，与其最大孩子互换。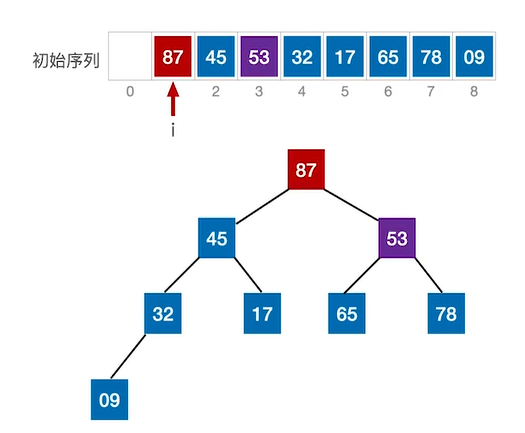
image.png
⑤互换后又有不满足大根堆的结点（53），再次进行互换
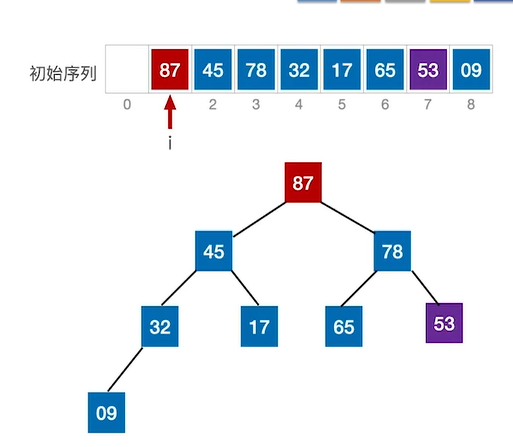
image.png
image.png
最终获得的大根堆如下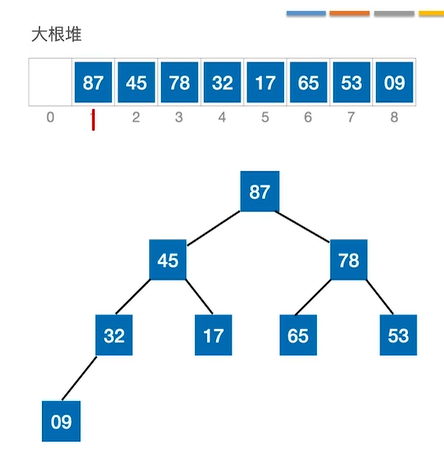
image.png

大根堆建立代码

image.png

基于大根堆的选择排序（堆排序）

每一趟把堆顶元素，与待排序的中的最后一个元素进行交换。
如上面例子中，则需将87和9交换，交换后87的最终位置确定，此后再做大根堆的建立和堆排序不需要再考虑87。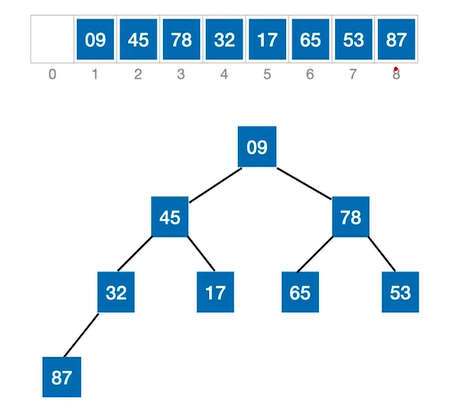
image.png
交换后不再是大根堆，需要重新进行大根堆的建立，将交换后的堆顶元素不断下坠。调整结果如下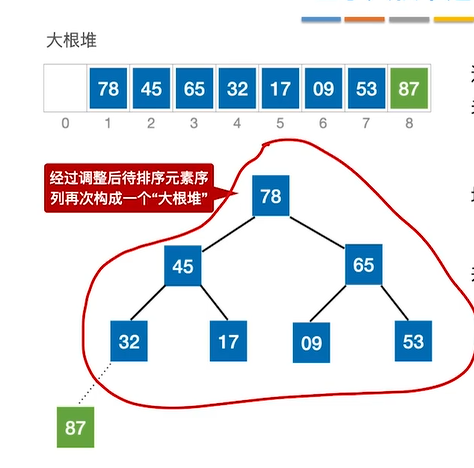
image.png
第一趟处理结束
此后的处理如上。
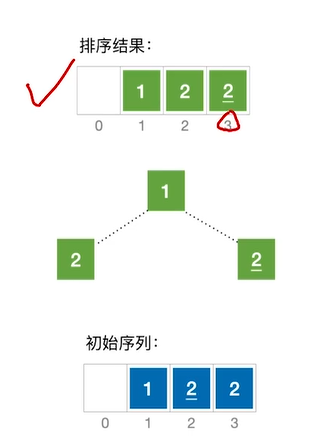
最终排序结果如下: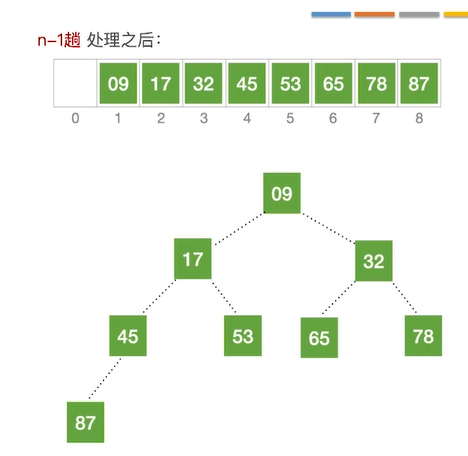
image.png

排序代码

image.png

算法效率总结

建立初始堆的时间复杂度:image.png

根节点的下坠

时间复杂度O(logn)
image.png

整体时间复杂度

image.png

堆排序空间复杂度

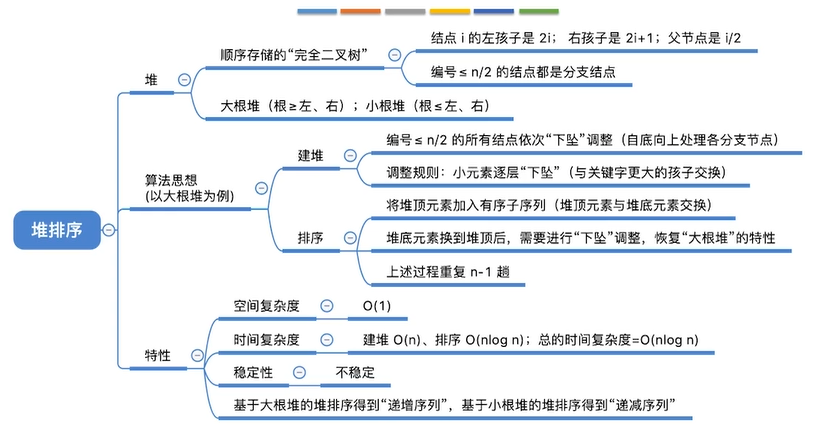
image.png

算法稳定性

不稳定
image.png

总结

image.png