石子合并

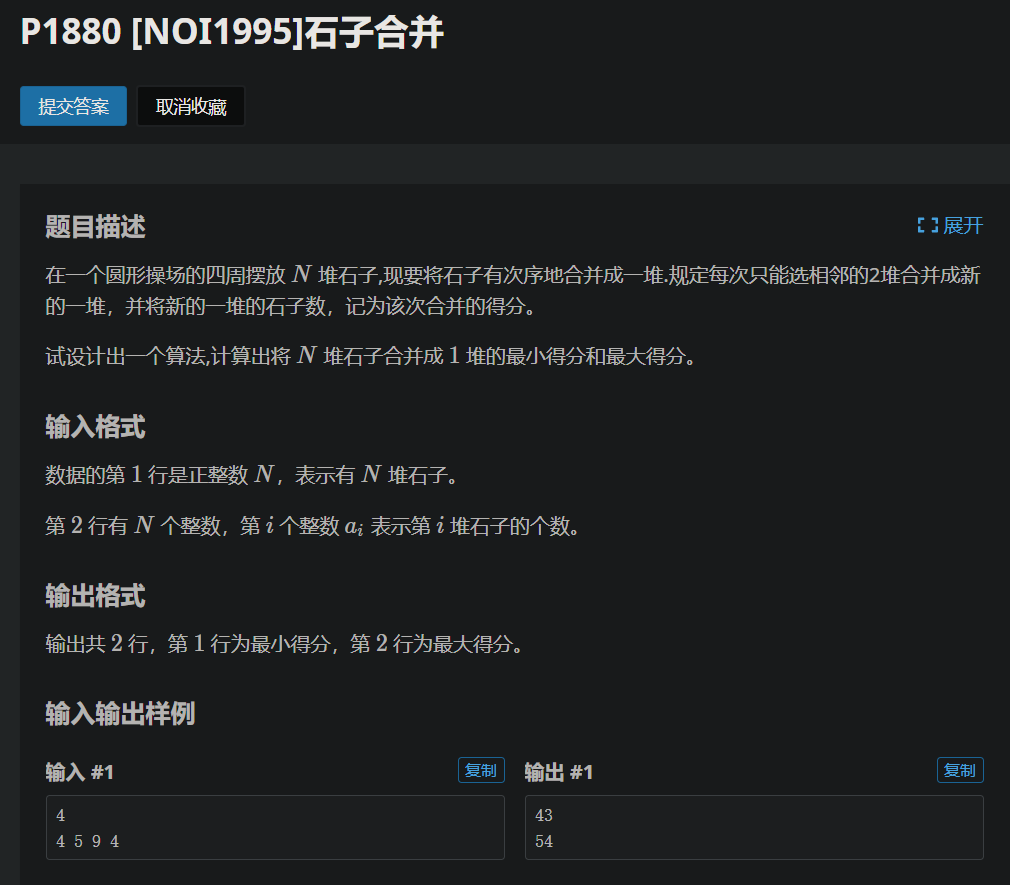
问题描述和样例

• 

  问题求解

  定义

1. arr[i] : 第i堆石子的个数
2. m[i][j][0/1] : 合并i-j堆的最大值(1)和最小值(0)
3. sum[i] : 第一堆到第i堆总和 , 用于求解区间和
   

   基础解

• 当只有一堆石子时 , 无需合并
  • m[i][i][0] = 0;
  • m[i][i][1] = 0;

• 由于是一个环, 所以最后的可以和最前边的合并 , 可以用一个2倍于原数组数组存放 , 可以覆盖到循环合并的所有情况

  递归求解

• 由于一堆石子时是基础解 ,所以从2堆石子时向上求解

• m[s][j][1] = ( sum[j] - sum[s - 1] ) + max { m[s][k - 1][1] + m[k][j][1] }
• m[s][j][0] = ( sum[j] - sum[s - 1] ) + min { m[s][k - 1][0] + m[k][j][0] }
  • k为所有可能的合并位置
  • ( sum[j] - sum[s - 1] ) , 表示此次合并的值 (arr[s] + arr[s+1] + ….. + arr[j] =sum[j] - sum[s - 1] )

代码

#include<stdio.h>
const int N = 202;//最大的堆数
int arr[N];
int n;//实际堆数
int m[N][N][2];//m[i][j][0] 合并i-j最小值   m[i][j][1] 合并i-j最大值 
int sum[N] = {0};//sum[i][j] = i到j的和
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &arr[i]);
        arr[n + i] = arr[i];
        //基础解  只有一堆无需合并
        m[i][i][0] = 0;
        m[i][i][1] = 0;
    }
    for (int i = 1; i <= 2 * n; i++) {
        sum[i] = sum[i - 1] + arr[i];
    }
    //动态规划
    for (int r = 2; r <= n; r++) {//合并的长度
        for (int s = 1; s <= n*2-r+1; s++) {//合并的起始点
            int j = s + r - 1;//合并的终点
            //初始化m[s][j]
            m[s][j][0] = m[s][s][0] + m[s + 1][j][0] + sum[j] - sum[s - 1];
            m[s][j][1] = m[s][s][1] + m[s + 1][j][1] + sum[j] - sum[s - 1];
            for (int k = s + 2; k <= j; k++) {
                //分割点k   表示分割 [i,k-1] [k,i+1] k∈[s+1,j-1]  左边界s s+1 s+1  右边界 j-1 j j
                if (m[s][j][0] > m[s][k - 1][0] + m[k][j][0] + sum[j] - sum[s - 1]) {
                    m[s][j][0] = m[s][k - 1][0] + m[k][j][0] + sum[j] - sum[s - 1];
                }
                if (m[s][j][1] < m[s][k - 1][1] + m[k][j][1] + sum[j] - sum[s - 1]) {
                    m[s][j][1] = m[s][k - 1][1] + m[k][j][1] + sum[j] - sum[s - 1];
                }
            }
        }
    }
    //获得最优解
    int max = m[1][n][1];
    int min = m[1][n][0];
    for (int i = 2; i <= n; i++) {
        if (max < m[i][i + n - 1][1]) {
            max = m[i][i + n - 1][1];
        }
        if (min > m[i][i + n - 1][0]) {
            min = m[i][i + n - 1][0];
        }
    }
    printf("%d\n%d", min,max );
    return 0;
}