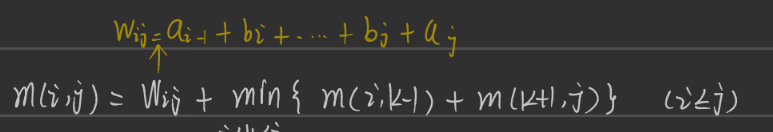Draft(1).pdf

题目描述

T 是由有序集合S = {X ，X ……, X ) (X <X ……,<X) 构成的二叉搜索树 在其中查找某个值

  • X ∈ (Xi, Xi+1) 的概率为 ai
  • X = Xi 的概率为bi

规定 x0 = -∞ , Xn+1 = +∞ ,

存取分布概率

  • 称 (a0 , b1 ,a1 , ….. , bn , an ) 为集合S的存取概率分布

image.png

平均路长

  • image.png
  • 当S确定时具有平均最小路长的T就是对应的最优二叉树

递归求解最优值

定义

  1. W[i]: a0 + b1 + a1 + ……. + bi + ai
  2. w[i][j] : a + bi + ai + ……. + bj + aj
  3. a[i] : (xi-1, xi) 的存取概率
  4. b[i] : xi 的存取概率
  5. root[i][j] : 当子树为T时的根节点
  6. m[i][j] :当子树为T是后的
    基础解

  • 当只有一个非叶节点时, 其平均路长只可以是 ai-1 + bi + ai ,节点为Xi , m[i][i] = W[i][i]

    递归解

  • image.png

    原问题解

  • m[1][n]

代码

  1. /*
  2. 设 S={x1, x2, ···, xn}  是一个有序集合，且x1, x2, ···, xn表示有序集合的二叉搜索树利用二叉树的顶点存储有序集中的元素，而且具有性质：存储于每个顶点中的元素x 大于其左子树中任一个顶点中存储的元素，小于其右子树中任意顶点中存储的元素。
  4. 最优二叉树就是平均路长最小的数
  5. */
  6. #include<stdio.h>
  7. #include<stdlib.h>
  8. const int N = 100;
  9. double w[N][N];//w[i][j]=ai-1 + bi + .... + bj + aj
  10. double m[N][N];//m[i][j] = w[i][j]P(ij)
  11. int n;//元素个数
  12. double a[N];//失败概率
  13. double b[N];//失败概率
  14. int root[N][N];//当子树Tij 最优时候的根节点在S中的下标
  15. int q = 0;
  16. double W[N];
  18. //显示解的树形结构
  19. void showTree(int l,int r,int deep) {
  20.     if (l > r) {
  21.         for (int i = 0; i < deep; i++) {
  22.             printf("-");
  23.         }
  24.         printf("q%d\n",q++);
  25.         return;
  26.     }
  27.     for (int i = 0; i < deep; i++) {
  28.         printf("-");
  29.     }
  30.     printf("%d\n",root[l][r]);
  31.     showTree(l, root[l][r] - 1, deep + 1);
  32.     showTree( root[l][r] + 1,r, deep + 1);
  33. }
  36. //计算 a[i-1] + b[i] + a[i] + ..... + b[j] + a[h]
  37. double getW(int i, int j) {
  38.     return W[j] - W[i - 1] + a[i - 1];
  39. }
  42. int main() {
  43.     //输入
  44.     scanf("%d", &n);
  45.     scanf("%lf", &a[0]);//输入a0
  46.     W[0] = a[0];
  47.     for (int i = 1; i <=n; i++) { // b1 , a1, ... bn , an 
  48.         scanf("%lf", &b[i]);
  49.         scanf("%lf", &a[i]);
  50.         W[i] = W[i - 1] + a[i] + b[i];//用来求解区间和
  51.     }
  53.     //初始化 当非叶节点个数为1时
  54.     for (int i = 1; i <= n; i++) {
  55.         w[i][i] = a[i - 1] + a[i] + b[i];
  56.         m[i][i] = w[i][i];
  57.         root[i][i] = i;
  58.     }
  60.     //动态规划
  61.     for (int r = 2; r <= n; r++) {//子树非叶节点个数
  62.         for (int i = 1; i <= n - r + 1; i++) {//子树起点
  63.             int j = i + r - 1;//子树终点
  64.             root[i][j] = i;
  65.             m[i][j] = 0xFFFFFF;
  66.             for (int k = i; k <= j; k++) {//轮流作为根节点
  67.                 if (m[i][j] > getW(i,j) + m[i][k - 1] + m[k + 1][j]) {
  68.                     root[i][j] = k;
  69.                     m[i][j] = getW(i, j) + m[i][k - 1] + m[k + 1][j];
  70.                 }
  71.             }
  72.         }
  73.     }
  74.     //输出最短平均路径m[1][n]
  75.     printf("%.2lf\n", m[1][n]);
  77.     //表达树
  78.     showTree(1,n,1);
  79.     return 0;
  80. }
  • 输入样例

3
0.15 0.5 0.1 0.1 0.05 0.05 0.05

  • 输出

1.50
-1
—q0
—2
—-q1
—-3
——q2
——q3

image.png

  1. #include<stdio.h>
  2. #include<stdlib.h>
  3. const int N = 100;
  4. double w[N][N];//w[i][j]=ai-1 + bi + .... + bj + aj
  5. double m[N][N];//m[i][j] = w[i][j]P(ij)
  6. int n;//元素个数
  7. double a[N];//失败概率
  8. double b[N];//失败概率
  9. int root[N][N];//当子树Tij 最优时候的根节点在S中的下标
  10. int q = 0;
  11. double W[N];//用来区间求和  w[i][j] =  a[i-1] + b[i] + a[i] + ..... + b[j] + a[h] = W[j] - W[i - 1] + a[i - 1]
  12. void showTree(int l,int r,int deep) {
  13.     if (l > r) {
  14.         for (int i = 0; i < deep; i++) {
  15.             printf("-");
  16.         }
  17.         printf("q%d\n",q++);
  18.         return;
  19.     }
  20.     for (int i = 0; i < deep; i++) {
  21.         printf("-");
  22.     }
  23.     printf("%d\n",root[l][r]);
  24.     showTree(l, root[l][r] - 1, deep + 1);
  25.     showTree( root[l][r] + 1,r, deep + 1);
  26. }
  27. //计算 a[i-1] + b[i] + a[i] + ..... + b[j] + a[h]
  28. double getW(int i, int j) {
  29.     return W[j] - W[i - 1] + a[i - 1];
  30. }
  31. int main() {
  32.     //输入
  33.     scanf("%d", &n);
  34.     scanf("%lf", &a[0]);//输入a0
  35.     W[0] = a[0];
  36.     for (int i = 1; i <=n; i++) { // b1 , a1, ... bn , an 
  37.         scanf("%lf", &b[i]);
  38.         scanf("%lf", &a[i]);
  39.         W[i] = W[i - 1] + a[i] + b[i];
  40.     }
  41.     //查看输入
  42.     printf("\n");
  43.     printf("a : ");
  44.     for (int i = 0; i <= n; i++) {
  45.         printf("%.2lf ", a[i]);
  46.     }
  47.     printf("\n");
  48.     printf("b : ");
  49.     for (int i = 1; i <= n; i++) {
  50.         printf("%.2lf ", b[i]);
  51.     }
  52.     printf("\n");
  54.     //初始化
  55.     for (int i = 1; i <= n; i++) {
  56.         w[i][i] = a[i - 1] + a[i] + b[i];//
  57.         m[i][i] = w[i][i];
  58.         root[i][i] = i;
  59.     }
  60.     //动态规划
  61.     for (int r = 2; r <= n; r++) {//子树非叶节点个数
  62.         for (int i = 1; i <= n - r + 1; i++) {//子树起点
  63.             int j = i + r - 1;//子树终点
  64.             root[i][j] = i;
  65.             m[i][j] = 0xFFFFFF;
  66.             for (int k = i; k <= j; k++) {//轮流作为根节点
  67.                 if (m[i][j] > getW(i,j) + m[i][k - 1] + m[k + 1][j]) {
  68.                     root[i][j] = k;
  69.                     m[i][j] = getW(i, j) + m[i][k - 1] + m[k + 1][j];
  70.                 }
  71.             }
  72.         }
  73.     }
  74.     //输出最短平均路径m[1][n]
  75.     printf("%.2lf\n", m[1][n]);
  77.     //显示w 和 m
  78.     for (int i = 1; i <= n; i++) {
  79.         for (int j = 1; j <= n; j++) {
  80.             printf("%.2lf ", m[i][j]);
  81.         }
  82.         printf("\n");
  83.     }
  84.     printf("\n"); printf("\n");
  85.     for (int i = 1; i <= n; i++) {
  86.         for (int j = 1; j <= n; j++) {
  87.             printf("%4.2lf ", getW(i,j));
  88.         }
  89.         printf("\n");
  90.     }
  92.     //表达树
  93.     showTree(1,n,1);
  94.     return 0;
  95. }

作业 :

  • 1.设n=4，有序集为k1, k2, k3, k4，存取概率设b(1 : 4)=(3, 3, 1, 1)和a(0 : 4)=(2,3,1,1,1)写出构造最优二叉搜索树的过程。

  • 输入 :

    4 2 3 3 3 1 1 1 1 1

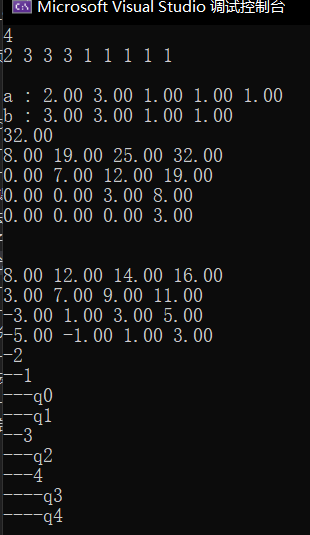
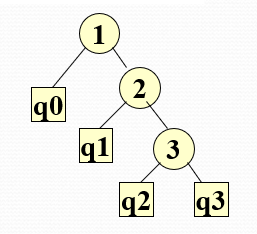
  • 输出 :

    • image.png

—注意：b,a都乘了16。

  • image.png
  • image.png