问题描述

  • 给定一个数组(有重复元素), 在O(n)时间内找到第k小的元素

    算法描述

  1. 将n个元素分成n/5组
    1. 且各个组内分别排序 ,
    2. 取出各组的中位数,共n/5个
  2. 递归的调用1 , 找出n个元素中的类似中位数(中位数的中位数)
  3. 通过该中位数划分原数组
  4. 将原数组左右两侧的与该中位数等值的元素聚集(解决有重复元素)
    1. 注意 左边的放到左边 , 右边的放到右边
  5. 现在 中位数等值集合的位置,就是排好序之后的位置 , 也就是可以单独确定出中位数的第几小的值 , 将中位数集合下标和 目标K值比较
    1. 如果K值落在中位数集合中 , 则改中位数就是第k小的元素
    2. 如果K小于中位数的位置 , 则递归的在左边子序列找第k小的元素
    3. 如果k大于中位数的位置 , 则递归的在右边子序列找第k - (当前中位数及中位数左边元素的个数) 小的元素

算法分析

  • 证明该算法可以在O(n)时间内找到第k小的元素
  • 将n个元素分成 n/5 个小组 , 组内排序 , 找到中位数的中位数, 作为划分基准
    • 组内排序每组 O(1) , 共有n/5个组
    • 中组内中位数 T(n/5)
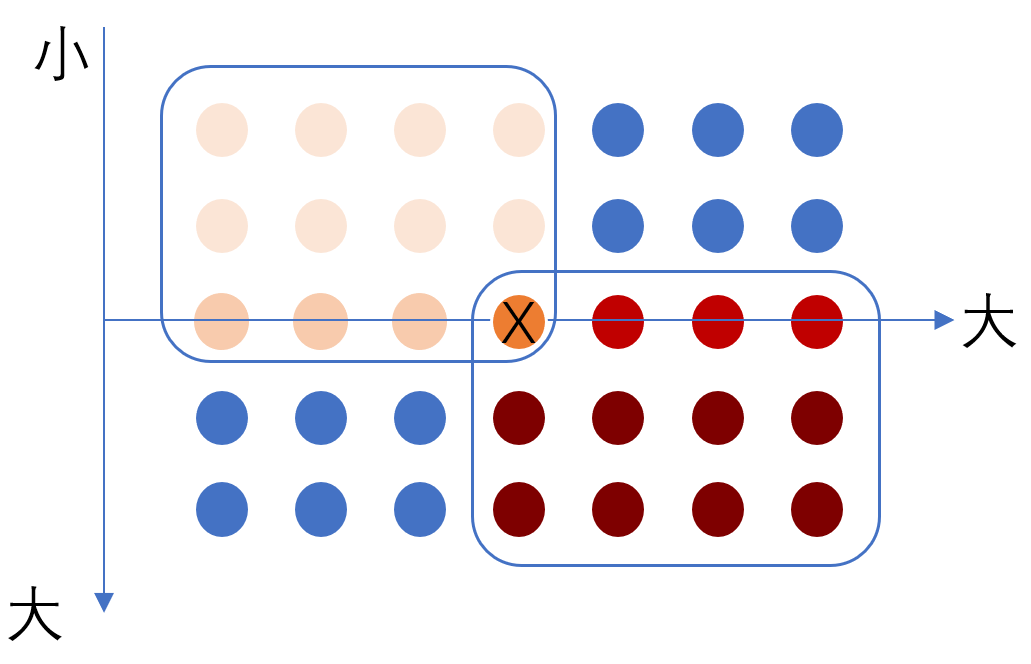
    • image.png
    • 图中X一定大于同行左边的中位数 , 故一定大于其通组内小于中位数的两个数 ,
      • 则X至少大于3(n/5/2) = 3n/10个元素 ,
        • 则之多大于 7n/10 个元素
    • 故当前问题的子问题规模最大不超过 7n/10 T(n)=T(7n/10) + …
  • 找到中位数的中位数X之后 , 对当前问题数组划分 , 划分操作复杂度为 o(n)
  • 综上递归式为 T(n) = T(n/5) + T(7n/10) + Cn

    T(n) = T(n/5) + T(7n/10) + CO(n) 数学归纳法 : 假设 : T(n) = O(n) 则

代码

  1. #include<stdio.h>
  2. #include<time.h>
  3. #include<stdlib.h>
  4. #include<algorithm>
  5. #include<time.h>
  6. using namespace std;
  7. //数组元素个数
  8. const int N = 500;
  9. //元素最大值
  10. const int MAX = 500;
  11. bool cmp(int a, int b) {
  12.     return a < b;
  13. }
  14. void swap(int a[], int c, int d) {
  15.     int t = a[c];
  16.     a[c] = a[d];
  17.     a[d] = t;
  18. }
  19. //小数组数组  排序范围左  排序范围右  交换目标 
  20. void sortandswap(int a[], int p, int r, int tar) {
  21.     //选择排序 
  22.     int max;
  23.     //只需要找打第三大的 (组内中位数) 
  24.     for (int i = 0; i <= r - p - 2; i++) {
  25.         max = p;//默认最大值的为第一个 
  26.         for (int j = p + 1; j <= r - i; j++) {//在未排序的获得最大的 
  27.             if (a[j] > a[max]) {
  28.                 max = j;
  29.             }
  30.         }
  31.         swap(a, max, r - i);
  32.         if (i == 2) {//找到组内中位数 
  33.             break;
  34.         }
  35.     }
  36.     swap(a, tar, p + 2);
  37. }
  38. //将和主元的值相同的元素集中
  39. int Amass(int a[], int p, int r, int pivort, int& p1, int& pr) {
  40.     int num1 = 0, num2 = 0;
  42.     for (int i = p; i <= r; i++) {
  43.         if (a[i] == a[pivort] && i != pivort) {
  44.             if (i < pivort - num1) {//左边重复的
  45.                 num1++;
  46.                 swap(a, i, pivort - num1);
  47.             }
  48.             else if (i > pivort + num2) {//右边重复的
  49.                 num2++;
  50.                 swap(a, i, pivort + num2);
  51.             }
  53.         }
  54.     }
  55.     p1 = pivort - num1;
  56.     pr = pivort + num2;
  57.     return num1 + num2;
  58. }
  59. //根据主元划分 返回主元下标
  60. int partition(int a[], int p, int r, int pivort) {
  61.     //将基准放到最左边
  62.     swap(a, p, pivort);
  63.     int i = p, j = r + 1, x = a[p];
  64.     while (1) {
  65.         while (a[++i] < a[p] && i <= r);
  66.         while (a[--j] > a[p]);
  67.         if (i >= j) {
  68.             break;
  69.         }
  70.         swap(a, i, j);
  71.     }
  72.     a[p] = a[j];
  73.     a[j] = x;
  74.     return j;
  75. }
  76. //在数组a,a[p:r] 序列中找到第k小的元素  (!!!即排序后下标为a[p+k-1])的元素 
  77. int Select(int a[], int p, int r, int k) {
  78.     if (r - p < 75) {
  79.         //直接排序,然后返回 
  80.         sort(a + p, a + r + 1, cmp);
  81.         return p + k - 1;
  82.     }
  83.     else {
  84.         //将a[p+i*5 : p+i*5+4] 中的中位数和a[p+i] 交换位置 
  85.         for (int i = 0; i <= (r - p - 4) / 5; i++) {
  86.             sortandswap(a, p + i * 5, p + i * 5 + 4, p + i);
  87.         }
  88.         //找到中位数集合a[p:p+(r-p-4)/5]的中位数  pivort为下标 
  89.         int pivort = Select(a, p, p + (r - p - 4) / 5, (r - p - 4) / 10);
  90.         //根据中位数的中位数划分数组
  91.         pivort = partition(a, p, r, pivort);
  92.         //TODO 集中和a[pivort]相等的元素到一起 , 到a[pivort : pivort+m] , m 为除了a[pivort]之外相等的元素个数 
  93.         int pl, pr;
  94.         int m = Amass(a, p, r, pivort, pl, pr);
  95.         //判断是否需要继续递归寻找
  96.         int j = pl - p; //小于pivort的个数
  97.         if (k > pl - p && k <= pr - p + 1) {
  98.             return pl;
  99.         }
  100.         else if (k <= pl - p) {//在左边找
  101.             return Select(a, p, pl - 1, k);
  102.         }
  103.         else if (k > pr - p + 1) {//在右边找
  104.             return Select(a, pr + 1, r, k - (pr - p + 1));
  105.         }
  106.     }
  107. }
  108. int main()
  109. {
  110.     while (1) {
  111.         //随机填充数组
  112.         srand(time(NULL));
  113.         int a[N];
  114.         for (int i = 0; i < N; i++) {
  115.             a[i] = rand() % MAX;
  116.         }
  118.         //随机取得第k大的元素 
  119.         int k = rand() % N;
  121.         //获得结果
  122.         printf("------------------------------------------------------\n");
  123.         printf("k : %d\n",k);
  124.         int resIndex = Select(a, 0, N - 1, k);
  125.         int res = a[resIndex];
  126.         //校验并输出(对数组排序,并获取a[k-1]) 作为校验值 
  127.         sort(a, a+ N, cmp);
  128.         int verify = a[k - 1];
  129.         if (verify != res) {//校验
  130.             printf("not equ! %d %d\n",res,verify);
  131.         }
  132.         else {
  133.             printf("第%d小的元素为 : %d \t校验 : %d", k,res, verify);
  134.         }
  135.         system("pause");
  136.     }
  139.     return 0;
  140. }