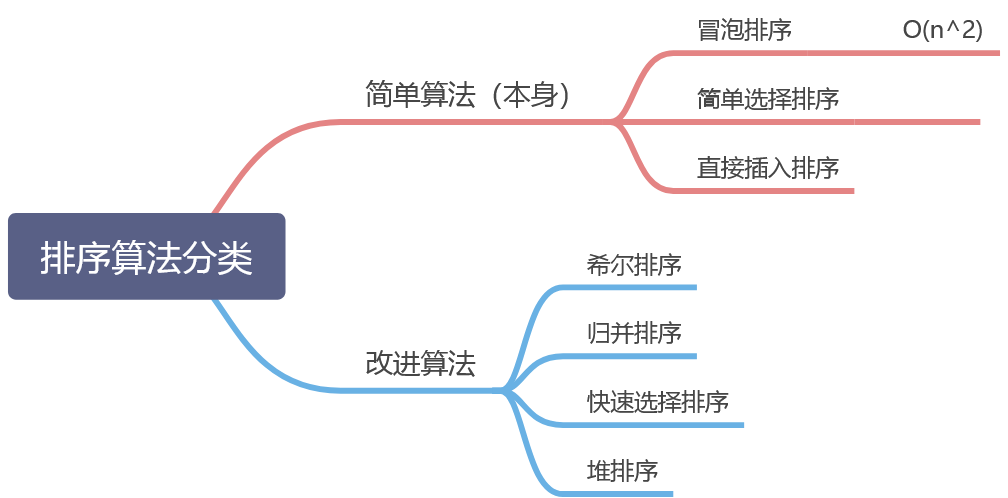
大话数据结构 | 排序 - 图1大话数据结构 | 排序 - 图2```c //非规范的冒泡排序，从头开始，一般是相邻比较，大的往后，一轮下来到靠后位置

include”stdio.h”

define MAXSIZE 10

void swap(int a,int b) { int t; t=a; a=b; b=t; } void Bubblesort(int *a) { for(int j=0;j<9;j++) { for(int i=1;i=MAXSIZE-j为一趟，内循环9=j趟为n-1 { if(a[i]>a[i+1]) //本身有序时，则比较次数为0，即0交换 //10数据比较9次，9个数据比较8次….9+8+7+…+1=n(n-1)/2 swap(&a[i],&a[i+1]); } } } int main() { int a[MAXSIZE+1]={0,1,4,5,6,7,8,9,10,2,3}; Bubblesort(a); for(int i=1;i<=MAXSIZE;i++) { printf(“%d “,a[i]); } }

  1. ```c
  2. //规范的冒泡排序，从头开始，一般是相邻比较，小的往上冒，一趟下来有一个小的产生
  3. #include"stdio.h"
  4. #define MAXSIZE 10
  5. typedef struct 
  6. {
  7.   int key;
  8. }Redtype;//一个Redtype其实就相当于一个int 
  9. typedef struct 
  10. {
  11.   Redtype * r;//r[0]空出来
  12.   int length;
  13. }Sqlist;
  14. void swap(int *a,int *b)
  15. {
  16.     int t;
  17.     t=*a;
  18.     *a=*b;
  19.     *b=t;
  20. }
  21. void Bubblesort(Sqlist *L)
  22. { for(int j=0;j<9;j++)
  23.  {
  24.     for(int i=L->length-1;i>=1;i--)//从末尾开始
  25.     {
  26.         if(L->r[i+1]<L->r[i])          //后一个比前一个小，则交换
  27.                                //10数据比较9次，9个数据比较8次....9+8+7+...+1=n(n-1)/2
  28.         swap(&L->r[i],&L->r[i+1]);
  29.     }
  30.  }
  31. }
  32. //最好情况：有序：0交换，比较次数：未改进是9+8+7....+1,逆序：比较交换次数均是9+8+7+...+1
  33. int main()
  34. {
  35. int a[MAXSIZE+1]={0,1,4,5,6,7,8,9,10,2,3};
  36. Sqlist L;
  37. L.length=10;
  38. L.r=a;
  39. Bubblesort(&L);
  40.    for(int i=1;i<=L.length;i++)
  41.   {
  42.     printf("%d ",L.r[i]);
  43.   }
  44. }
  1. //最终版的冒泡排序
  2. #include<stdio.h>
  3. #define MAXSIZE 10
  4. typedef struct 
  5. {
  6.   int key;
  7. }Redtype;//一个Redtype其实就相当于一个int 
  8. typedef struct 
  9. {
  10.   Redtype * r;//r[0]空出来
  11.   int length;
  12. }Sqlist;
  13. void swap(Redtype *a,Redtype *b) 
  14. {
  15.     Redtype t;
  16.     t=*a;
  17.     *a=*b;
  18.     *b=t;
  19. }
  20. void Bubblesort(Sqlist *L)
  21. { 
  22.   int flag=1;//先设置为1
  23.   for(int j=0;j<L->length-1&&flag;j++)
  24.  {
  25.      flag=0;//没有交换,flag的值为0，提前终止
  26.     for(int i=L->length-1;i>=1+j;i--)//从末尾开始,i>1+j理解上是为了减少没必要的排序
  27.     {
  28.         if(L->r[i+1].key<L->r[i].key)          //后一个比前一个小，则交换
  29.         {swap(&L->r[i],&L->r[i+1]);
  30.         flag=1;//发生交换
  31.         }
  33.     }
  34.  }
  35. }
  36. //改进后：最好正序，比较n-1次->O(n)，交换0次,最坏9+8+7+...1->比较=交换=n-1+...1，时间复杂度为O(n^2)
  38. int main()
  39. {
  40. int a[MAXSIZE+1]={0,1,4,5,6,7,8,9,10,2,3};
  41. Sqlist L;
  42. L.length=10;
  43. L.r=(Redtype*)a;//左右类型一样
  44. Bubblesort(&L);
  45.    for(int i=1;i<=L.length;i++)
  46.   {
  47.     printf("%d ",L.r[i]);
  48.   }
  49. }
  53. //简单选择排序：每一次在n-i+1个,ri....rn个中找到合适的与之交换
  54. #include "stdio.h"
  55. #define MAXSIZE 10
  56. typedef struct 
  57. {
  58.   int key;
  60. }Redtype;
  61. typedef struct 
  62. {
  63.   Redtype * r;
  64.   int length ;
  65. }Sqlist;
  66. void swap(Redtype *a,Redtype *b);//交换操作
  67. void Simplesort(Sqlist *L);//简单选择排序
  68. void SortPrint(Sqlist *L);
  70. int main()
  71. {
  72.   Sqlist L;
  73.   int a[MAXSIZE+1]={0,1,3,5,7,9,2,4,6,8,10};
  74.   L.length=MAXSIZE;
  75.   L.r=(Redtype*)a;
  76.   Simplesort(&L);
  77.   SortPrint(&L);
  78. }
  79. void swap(Redtype *a,Redtype *b)
  80. {
  81.   Redtype t;
  82.   t=*a;
  83.   *a=*b;
  84.   *b=t; 
  85. }
  86. void Simplesort(Sqlist *L)
  87. { int j;
  88. for(j=1;j<=L->length-1;j++)//n个数据,交换n-1次
  89.   { //寻找合适的位置，从n-i+1中寻找
  90.  int min=j;//设置下标 1:2-10,2:3-7...9：10  9+8+7+6...+1 n*(n-1)/2
  91.  int k;
  92.    for(int i=j+1;i<=L->length;i++)
  93.    {
  95.    if(L->r[i].key<=L->r[min].key)
  96.      {
  97.      min=i;//记录找到的位置，更新最小值
  98.      }
  100.    }
  101. swap(&L->r[min],&L->r[j]);
  102.   }
  103. }
  105. /*
  106.  *n-i+1,最好和最坏：第i趟，n-i比较，总和n*(n-1)/2次
  107.  *交换次数最好0次，最坏同比较
  108.  *总复杂度O(n*2)
  109.  */
  110. void SortPrint(Sqlist *L)
  111. {
  112.   for(int i=1;i<=L->length;i++)
  113.   {
  114.     printf("%d ",L->r[i].key);
  115.   }
  116. }
  117. //时间复杂度同冒泡排序，但是略优于冒泡排序
  126. //直接插入排序算法：哨兵 is important 作为辅助空间和判断依据
  127. #include"stdio.h"
  128. #define MAXSIZE 10
  129. typedef struct 
  130. {
  131.   int key;
  132. }Redtype;
  133. typedef struct 
  134. {
  135.   Redtype * r;
  136.   int length;
  137. }Sqlist;
  138. void StrInsertsort(Sqlist * L);
  139. void LinkPrint(Sqlist *L);
  140. int main()
  141. {
  142.   int a[MAXSIZE+1]={0,2,4,6,8,10,1,3,5,7,9};
  143.   Sqlist L;
  144.   L.r=(Redtype *)a;
  145.   L.length=MAXSIZE;
  146.   StrInsertsort(&L);
  147.   LinkPrint(&L);
  148.   return 0;
  149. }
  150. /*
  151.  *第一个元素默认在有序表中,所以考虑r2...rn这些位置
  152.  * 哨兵的作用为作为辅助空间和防止越界代替i>=0类似的写法;
  153.  * 注意的地方是两个for的写法
  154.  */
  155. void StrInsertsort(Sqlist *L)
  156. { int j;
  157. for(int i=2;i<=L->length;i++) //
  158. {
  159.   L->r[0].key=L->r[i].key;
  160. if(L->r[i].key<L->r[i-1].key)
  161.   {
  162.   for( j=i-1;L->r[0].key<L->r[j].key;j--) //重要点。
  163.    L->r[j+1]=L->r[j];
  164.    L->r[j+1]=L->r[0];
  165.   }
  166. }
  167. }
  168. /*
  169.  *
  170.  *时间复杂度分析：
  171.  *最好：正序:n-1外循环，内循环比较1次,最终为n-1个1相加，移动0次
  172.  *最坏：逆序：n-1趟，第k趟，移动k+2(哨兵的移动)次 3+4+5+...+n+1=(n+4)*(n-1)/2
  173.  *           比较次数 ，第k趟,比较k+1(for2)次，2+3+...+n=(n+2)*(n-1)/2
  174.  *           细节理解说明：for2:for( j=i-1;L->r[0].key<L->r[j].key;j--)
  175.  *           i-1；比较i次0与0也算一次
  176.  *           综合考虑：根据概率相同原则：平均比较和移动次数均是n^2/4
  177.  *            O(n^2)
  178.  *          同样的时间复杂度：直接插入排序比冒泡排序和简单选择排序更好一些
  179.  *          （一） 基本有序时，1+1+1+...kn(很少项较大)，移动kn，整体较小
  180.  *          （二）n较小，L->length较小，对n^2的影响较大，此时优势明显
  181.  */
  182. void LinkPrint(Sqlist *L)
  183. {
  184. for(int i=1;i<=L->length;i++)
  185. printf("%d ",L->r[i].key);
  186. }
  191. /*
  192.  *Shellsort ：希尔排序，优化后的直接插入排序，历史意义在于时间复杂度的突破
  193.  *直接插入排序的优势在于在数据基本有序，数量较少时这两个条件下，优势明显
  194.  *而希尔排序应创造这样的优势性条件，使数据变少和基本有序
  195.  *变少的有效措施是分割数据，及分组，在组内内部直接插入排序，如何分割
  196.  *在基本有序时在进行一次直接插入排序，基本有序，小的基本在前面，大的在后面，不大不小在中间
  197.  *算法核心:采用跳跃分割策略，保证基本有序而非局部有序
  198.  *
  199.  */
  200. #include"stdio.h"
  201. #define MAXSIZE 10
  202. typedef struct 
  203. {
  204. int key;
  205. }Redtype;
  206. typedef struct 
  207. {
  208.   Redtype *r;
  209.   int length;
  210. }Sqlist;
  211. void Shellsort(Sqlist *L);
  212. void StrInsertsort(Sqlist *L,int gap);
  213. void SortPrint(Sqlist *L);
  214. void swap(Redtype *a,Redtype *b);
  216. int main()
  217. {
  218.   Sqlist L;
  219.   int b=MAXSIZE;
  220.   int a[MAXSIZE+1]={0,9,8,7,6,5,1,2,3,4,10};
  221.   L.r=(Redtype*)a;
  222.   L.length=MAXSIZE;
  223.   Shellsort(&L);
  224.   SortPrint(&L);
  225.   return 0;
  226. }
  227. void Shellsort(Sqlist *L)
  228. {  int b=L->length/2;
  229.     while(b)
  230.  { 
  231.    StrInsertsort(L,b);
  232.    b/=2;
  233.  }
  234. }
  235. void StrInsertsort(Sqlist *L,int gap)
  236. { int i;
  237.    //printf("%d %d ",L->r[6].key,L->r[8].key);
  238.   for(i=1;i+gap<=L->length;i++)
  239.   { if(L->r[i].key>L->r[i+gap].key)//交换的条件***
  240.     swap(&(L->r[i]),&(L->r[i+gap]));
  241.   }  
  242. }
  243. //9,8,7,6,5,1,2,3,4,10
  244. /*  gap=5
  245.  *结尾=5:1,8,7,6,5,9,2,3,4,10
  246.  *   =6：1,2,7,6,5,9,8,3,4,10
  247.  *  =7:1,2,3,6,5,9,8,7,4,10
  248.  *  =8:1,2,3,4,5,9,8,7,6,10
  249.  *  =9:1,2,3,4,5,9,8,7,6,10
  250.  *  =10:1,2,3,4,5,9,8,7,6,10
  251.  * 
  252.  *  gap=2
  253.  *  1,2,3,4,5,9,8,7,6,10
  254.  *  1,2,3,4,5,7,8,9,6,10
  255.  *  1,2,3,4,5,7,6,9,8,10
  256.  * 
  257.  *  gap=1
  258.  *  1,2,3,4,5,6,7,9,8,10
  259.  *  1,2,3,4,5,6,7,8,9,10
  260.  */
  261. void swap(Redtype *a,Redtype *b)
  262. {
  263.   Redtype t;
  264.   t=*a;
  265.   *a=*b;
  266.   *b=t;
  268. }
  269. void SortPrint(Sqlist *L)
  270. {
  271.   for(int i=1;i<=L->length;i++)
  272.   printf("%d ",L->r[i].key);
  273.   printf("\n");
  274. }
/*堆排序:历史溯源：发明堆排序的人同样发明了对这样的数据结构：heap chunk
 * 了解大根堆和小根堆的概念
 * 简单选择排序：在n个元素中选择最小的需要比较n-1次，其中造成很多无效的比较
 * 而堆排序可以记录下来，规避简单选择排序的缺点，改进后的选择排序
 * 利用大根堆的
 * 问题数目不是完全二叉树的如何更变为大根堆,必须奇数个
 */
#include"stdio.h"
#define MAXSIZE 9
typedef struct
{
 int key;
}Redtype;
typedef struct
{
Redtype *r;
int length;
}Sqlist;
void HeapAdjust(Sqlist *L,int s,int m); //s是其实下标，m是末尾下标
void Heapsort(Sqlist *L);
void SortPrint(Sqlist *L);
void swap(Redtype *a,Redtype *b);//交换记录
int main()
{ int a[MAXSIZE+1]={0,5,1,9,3,7,4,8,6,2};
  Sqlist L;
  L.r=(Redtype*)a;
  L.length=MAXSIZE;
  Heapsort(&L);
  SortPrint(&L);
  return 0;
}
void SortPrint(Sqlist *L)
{
  for(int i=1;i<=L->length;i++)
  printf("%d ",L->r[i].key);

}
//核心的思想，子树的根节点及孩子的大小的比较
void HeapAdjust(Sqlist *L,int s,int m)
{
  int j;//temp的用途在于完成根与孩子的交换，存储元素，j的话与之相关的是2*j，2*j+1，左右孩子
  Redtype temp;
  temp=L->r[s];//由于在堆的实际排序中根节点很有用，记录根节点
  for(j=2*s;j<=m;j++)//孩子不超过n的范围
  {
  if(j<m&&L->r[j].key<L->r[j+1].key)
    j++;//j记录的是孩子中较大的那一方的下标
  if(temp.key>=L->r[j].key)//跟两个孩子中较大的比较之后，如果是大根堆，则打断循环
   break;
   //否则的话就赋值(此时有两个一样的数)
   L->r[s]=L->r[j];//j的角标那一项比较大
   s=j;
  }
  L->r[s]=temp;//如果进行了赋值，那就要想办法改变赋值的影响：即将temp赋值给新的s的位置
  //完成交换，这算法有些复杂
}

void Heapsort(Sqlist *L)
{
int i;
for(i=L->length/2;i>0;i--)//将一个无序列调整为大根堆，从n/2开始，比起小的均为分支节点
 HeapAdjust(L,i,L->length); //n
 //SortPrint(L);
 for(i=L->length;i>1;i--)
 {
 swap(&L->r[1],&L->r[i]);//堆顶与最后一个交换
 HeapAdjust(L,1,i-1);//生成数目减一的大根堆，从根节点开始调整

 }
}
//时间复杂度分析：主要操作为初始化堆和重建堆
/*  
 * 先来看初始化堆：堆的初始化主要是从最下层的分支节点与左右孩子比较，有必要时交换
 * 初始堆：最不利的情况是n/2*2=n次交换，时间复杂度O(n)
 * 在HeapAdjust中重建中时由于循环体j=2*j<=m，结合完全二叉树的性质即：从某一节点到根节点的距离log2i(向下取整)+1
 * j=2*j实际上和log2i+1循环次数相近，而Heapsort进行n-1的堆重建(伴随去n-1的堆顶记录)，综合在重建堆时的时间复杂度为O(n*logn)
 */
void swap(Redtype *a,Redtype *b)
{
  Redtype t;
   t=*a;
   *a=*b;
   *b=t;
}