1.从搜索引擎说起：
    机理略懂:依靠网络”蜘蛛”爬取分类，构建索引，供用户查找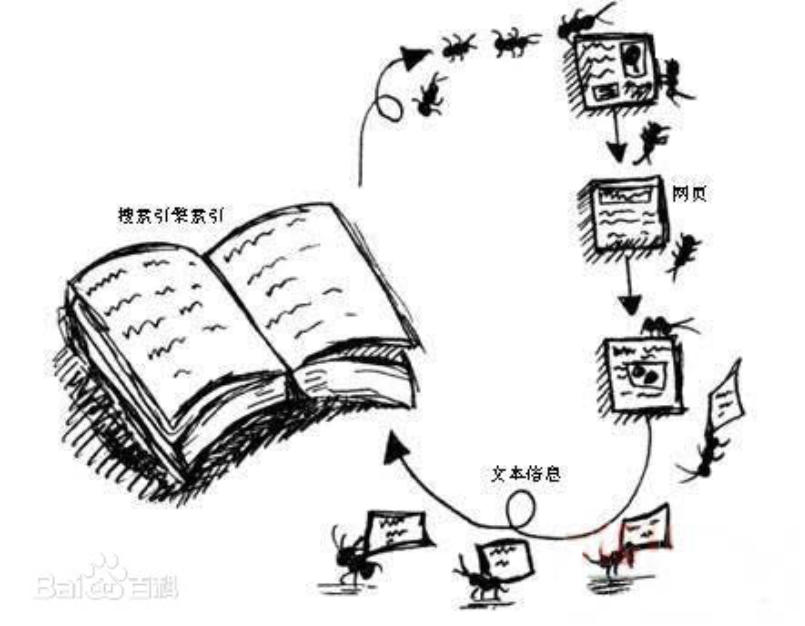
    图片.png
    2.查找
    查找表（Search Table）：被查数据元素（或记录）的集合。
    关键字（Key）:数据元素某个关键项的值，又称键值，（接触过SQL或PHP的话应该对键值熟悉）。比如数据库查询中id就是键值，当关键字唯一标识一个记录则是主关键字，可以识别多个数据元素的关键字是次关键字。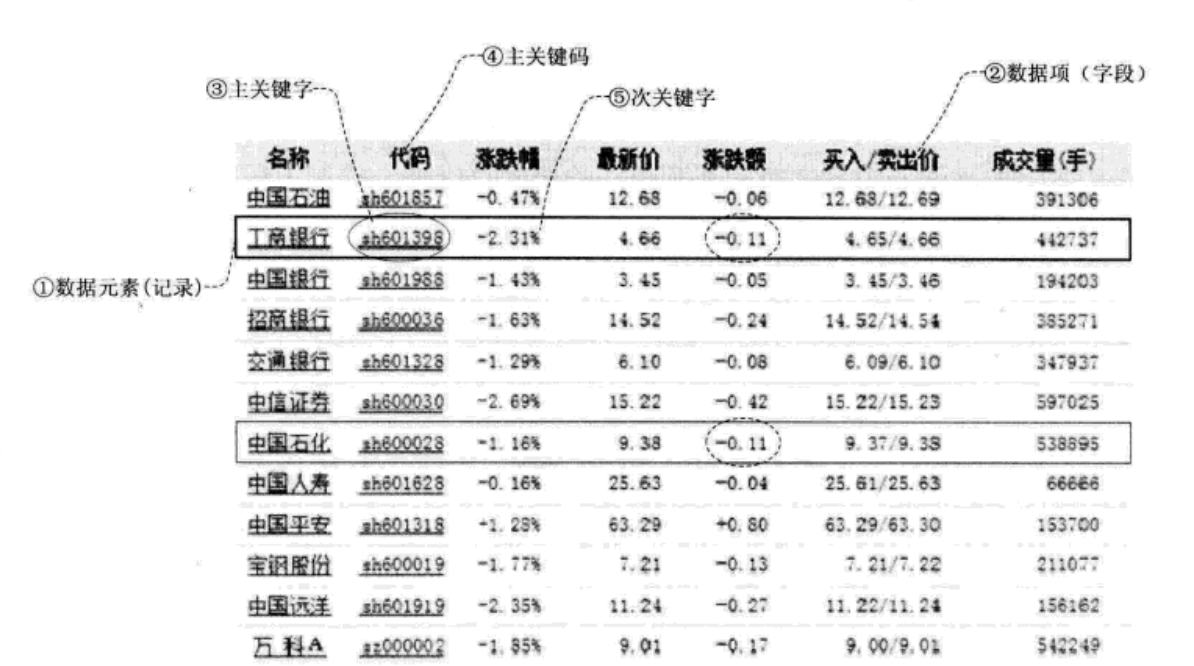
    图片.png
    3.查找表的分类：
    静态查找表：主要用于查找记录的位置或具体信息以及是否存在。
    动态查找表：主要用于记录查找时的插入，删除。
    静态查找表的例子：一段时间内表保持不变。（高考成绩表）。
    动态查找表的例子：注销非法用户&网络热词的添加。
    逻辑分析：查找基于的数据结构是集合，集合的记录之间本质上没有关系，因此想要获得较高的查找性能，就要改变数据元素之间的关系，建立表和树等结构。
    顺序表查找 | 摆放图书
    例子：散在地上的书[集合]，摆成一列整齐的书（很随意的摆）[线性表]，要查找某一本书，只能遍历查找。
    以上的例子就是对线性表进行查找属于静态查找表。
    顺序查找（Sequential Search）：又叫线性查找，讲从第一个（最后一个开始），逐一与给定的值比较。

    1. #include<stdio.h>
    2. #include<stdlib.h>
    3. /*a为数组，简单的线性表，n为记录个数，key是给定的关键字*/
    4. int Seqential_Search(int *a ,int n,int key)
    5. {
    6.     for(int i=1;i<=n;i++) //注意i从1开始，0是空出来的
    7.     {
    8.         if(a[i]==key)
    9.             return i;
    10.     }
    11. }
    12. int main()
    13. {
    15.  int a[5+1]={0,1,2,5,4,3};
    16.  int j=Seqential_Search(a,sizeof(a)/sizeof(int),5);
    17.  return j;
    18. }

    代码分析：这段代码很简单，i从1开始，但是却有缺陷，就是每次都有i<=n的比较来确保数组不会越界（题外话，数组越界可能会造成安全问题）。
    代码优化：设置哨兵则可以避免每次关注i<=n，a[0]设置为“哨兵”（给定的比较标准），a[1]~a[n]为记录的线性表，从n开始与a[0]比较,返回1~n则查找成功，否则返回0,查找失败。“哨兵”的好处在于数据规模很大时，效率的提高比较可观。
    代码时间复杂度分析（按有哨兵的分析）：查找成功：最优情况：比较1次就找到（比如在第n个），时间复杂度O（1），最坏情况：比较n次（在第1个），时间复杂度O（n）,查找失败：比较n+1次，时间复杂度O（n）.平均好查找次数(n+1)/2.时间复杂度还是O（n）.
    代码使用场景分析：当数据量很小时，比较适用，当数据规模较大时查找效率低下，另外根据代码的特点，可以将常用的数据放在前面（如果是有哨兵的就放后面），不常用的放后面以此来大幅提高效率。

    1. #include<stdio.h>
    2. #include<stdlib.h>
    3. /*含哨兵的顺序查找结构,避免对函数越界的担忧*/
    4. int Seqential_Search(int *a ,int n,int key)
    5. {   a[0]=key;//设置哨兵
    6.     int i=n;//从顺序表尾开始
    7.     while(a[i]!=key)
    8.         i--;
    9.     return i;//返回0说明查找失败
    10. }
    11. int main()
    12. {
    13.  int a[5+1]={0,1,2,5,4,3};
    14.  int j=Seqential_Search(a,5,5);
    15.  return j;
    16. }

    有序表查找 大话数据结构 | 查找 - 图3折半查找
    还是举书的例子，随机排成一列（线性表），按书名首字母排成一列（有序线性表），更有利于查找。
    例子切入：猜一个100以内的整数，要求用最少的次数猜出。
    折半查找：又叫二分查找（类似于二叉树的查找方法），要求线性表为有序线性表且为顺序存储（比如记录的关键码有序：从小到大），因为顺序存储具有随机访问的特性。主要思想就是取中间元素，如果与给定的值相等，则找到，比给定的值大于就找左半部分，比给定的值小就找右半部分，重复一开始的操作，直至找到。若查找区域无记录则查找失败。

    1. int Binary_Search(int*a ,int n,int key)
    2. {
    3.     int low,high,mid;
    4.     low=1;
    5.     high=n;
    7.     while(low<=high)
    8.    {
    9.     mid=(low+high)/2;/*折半更新mid的值*/
    10.     if(a[mid]<key) /*在右半部分，high不变，low为mid+1*/
    11.      low=mid+1;
    12.     else if(a[mid]>key)/*在左半部分，low不变,high为mid-1*/
    13.      high=mid-1;
    14.     else
    15.     return mid;/*相等返回位置信息*/
    16.    }
    18. }

    折半查找快速构建二叉树：
    以index为标准1-10是元素的位置，方块中的为[low,high],特点：右子树只改变左端点=mid+1.左子树只改变右端点=mid-1

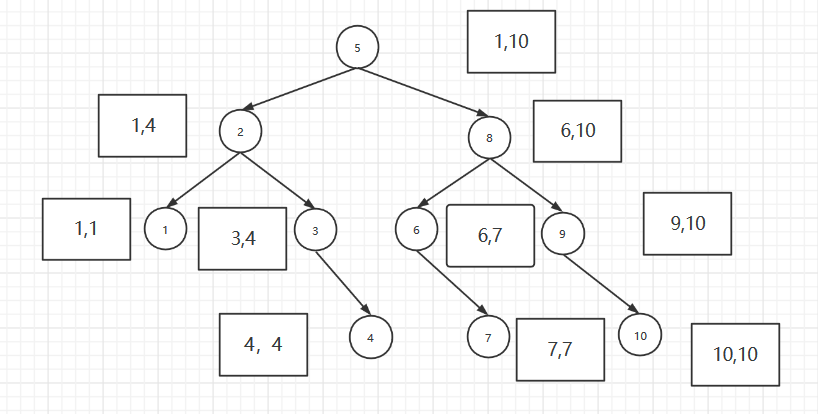
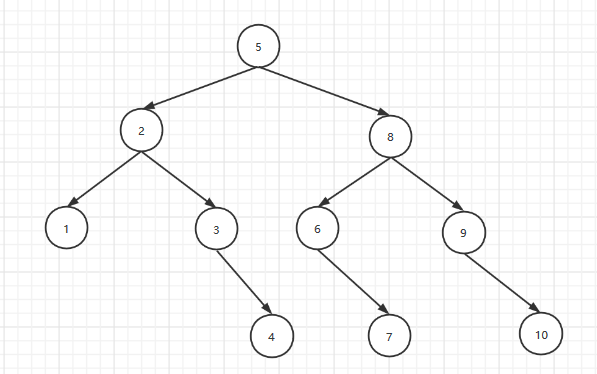
    图片.png
    图片.png
    参考
    算法分析：log2n向下去取整+1为层数，也是查找失败的次数，最好情况为1次。时间复杂度O（logn）
    插值查找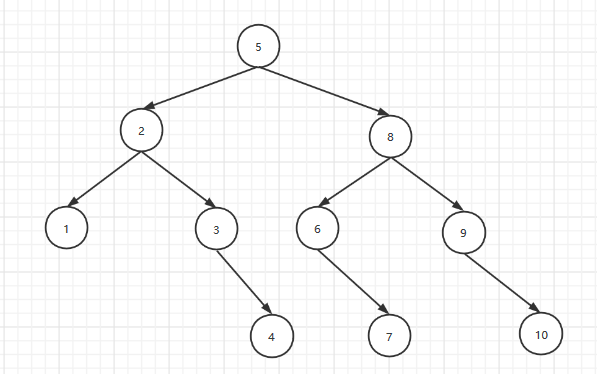
    大话数据结构 | 查找 - 图6
    如果找10,按折半查找四次，mid=(high-low)/2,适当变形为mid=low+1/2(high-low),
    这意味着是左端点+一半的区间，当换成左端点+适当区间，比如mid=low+(key-a[low]/a[high]-a[low])    [high-low],拿10来说只需要找一次，key-a[low]/a[high]-a[low]是插值查找的核心。
    算法适用场景：均匀的查找表，key-a[low]/a[high]-a[low]决定了如果遇到极端的数据{0,1,2000，…999999},比如key=2000,会导致第一查找偏后，这种情况下有悖插值算法的初衷，不太适用。
    斐波那契查找（Fibonacci Search）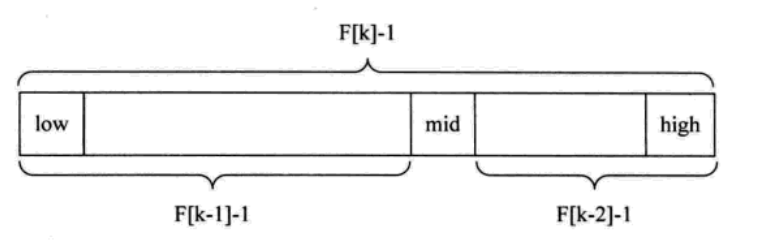
    图片.png
    斐波那契数列特征：F（k）=F(k-1)+F(k-2)
    图片.png

    1. #include"stdio.h"
    2. int F[11]={0,1,1,2,3,5,8,13,21,44,65};
    3. int Fibonacci_Search(int*a ,int n,int key)
    4. {
    5.     int low,high,mid,i,k;
    6.     low=1;//定义最低位
    7.     high=n;//定义最高位
    8.     k=0;
    9.     while(n>F[k]-1)
    10.     k++;  //计算n最斐波那契数列中的位置，全局数组的下标
    11.    for(i=n;i<=F[k]-1;i++)
    12.     a[i]=a[n];//填充至F[k]-1个，不足的用最后一个填充
    13.     while(low<=high)
    14.    {
    15.     mid=low+F[k-1]-1;//计算中间分割下标
    16.    if(key<a[mid])
    17.    {   high=mid-1;//最高值的移动
    18.        k--;
    19.    }
    20.    else if(key>a[mid])
    21.    {
    22.        low=mid+1;//最低值移动
    23.        k-=2;
    24.    }
    25.    else
    26.    {
    27.        if(mid<=n)
    28.        return mid;//存在在非补充区域
    29.        else
    30.        return n;  //mid>n说明为补全值,返回n
    31.    }
    32.    }
    35.     return 0;   
    36. }
    37. void main( )
    38. {
    39.     int a[11]={0,1,16,24,35,47,59,62,73,88,99};
    40.     int j=Fibonacci_Search(a,10,16);
    41.     printf("%d",j);   
    42. }

    图片.png
    算法分析：斐波那契查找的优势是确定在一个区域后会舍弃某一侧，时间复杂度为O(logn)，在平均性能上斐波那契数列查找优于折半查找。