回溯就是一个递归的过程

递归就一定是有中止的

回溯一般都是被抽象为一个N叉树

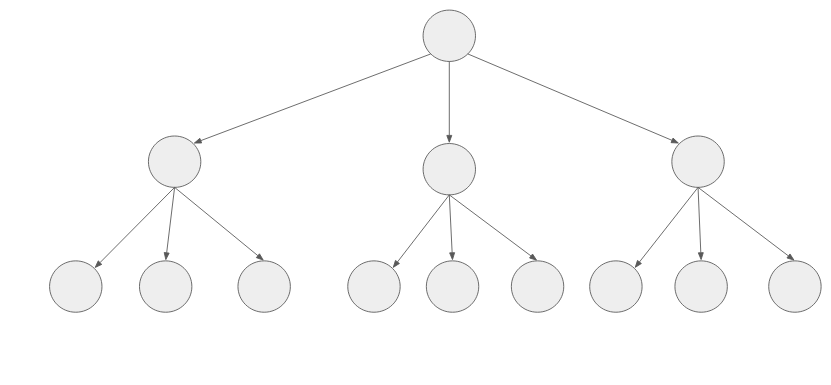
image.png

如上图所示：
树的宽度就是给定的集合的大小，通常是用for循环遍历的
树的深度就是递归来处理的

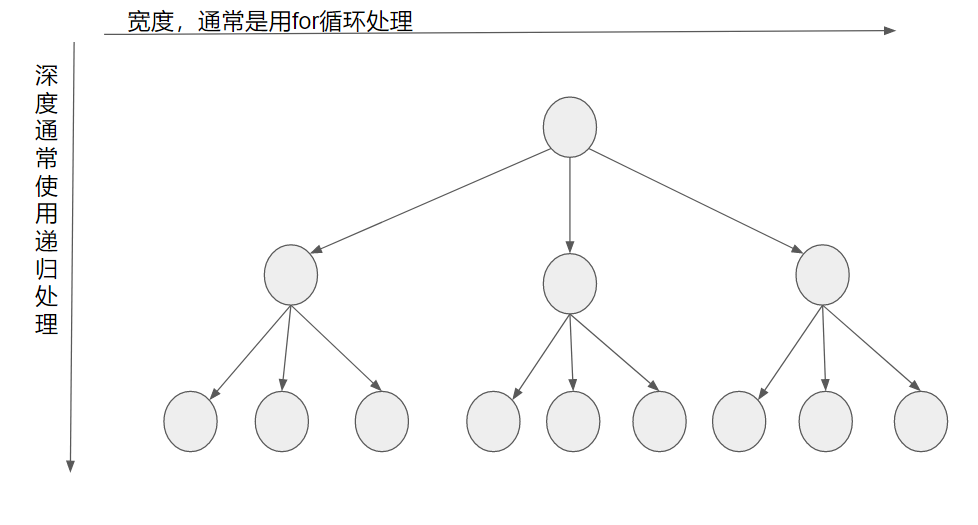
image.png
一般来说，递归方法都是没有返回值的

  2. void  递归方法名(参数){
  3.     if(终止条件){
  4.         收集结果;
  5.         return;
  6.     }
  8.     //单层搜索
  9.     for(集合元素){
  10.         处理节点；
  11.         递归函数；
  12.         回溯操作（撤销处理的情况）；//为什么要回溯可以看下面解释
  13.     }
  16.     return;
  17. }

为什么要回溯？

如果处理：{1，2，3，4} 第一次：1,2 只有回溯到1，的时候，才能把3加进来，得到：1,3 同样，只有1,3回溯一下，才能得到1，4

如果不回溯有什么后果？

如果不回溯，就会一直：1,2,3,4一直加下去

回溯之组合问题

例如：
力扣第77题，组合。
https://leetcode-cn.com/problems/combinations/

  1. 组合
    给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:

  1. [
  2. [2,4],
  3. [3,4],
  4. [2,3],
  5. [1,2],
  6. [1,3],
  7. [1,4],
  8. ]

从示例中可以看出，n=4就是代表的是：从1-4之间的数
{1，2，3，4}

k=2代表，从{1，2，3，4}中找出2个数组合的数

那么就得到了：

  1. [
  2. [2,4],
  3. [3,4],
  4. [2,3],
  5. [1,2],
  6. [1,3],
  7. [1,4],
  8. ]

1、如果找出k=2的，2个数的组合，我们可以写两个for循环，进行暴力，例如：

for(int i=0;i<size;i++){
    for(int j=i+1;j<size;j++){
        sout(i+""+j);
    }
}

2、如果找出k=3呢，3个数的组合，我们可以写三个for循环，进行暴力，例如：

for(int i=0;i<size;i++){
    for(int j=i+1;j<size;j++){
           for(int k=j+1;k<size;k++){
            sout(i+""+j+""+k);
            }
    }
}

如果k=100，k=1000呢？总不能写100个，1000个for循环吧。

那么就可以用回溯来解决这个问题。

回溯如何解决组合问题？