本章内容

  • 学习数据结构图来建立网络模型
  • 学习广度优先搜索
  • 学习有向图和无向图
  • 学习拓扑排序，这种排序与算法指出了节点之间的依赖关系。

小结

  • 广度优先算法指出是否有从A到B的路径。
    • 如果有，广度优先算法将找出最短路径。
  • 面临类似与寻找最短路径的问题时，可尝试使用图来建立模型，再使用广度优先搜索来解决问题。
  • 有向图中的边为箭头，箭头方向指明了关系的方向，例如，rama->adit 表示rama欠adit钱。
  • 无向图的边不带箭头，其中关系是双向的。
  • 队列是先进先出的。
  • 栈是后进先出的。
  • 你需要按加入顺序检测搜索列表中的人，否则找出的就不是最短路径，因此搜索列表必须是队列。
  • 对于检查过的人，务必不再去检查，否则可能导致无限循环。

练习

首先：最短距离的含义非常丰富。

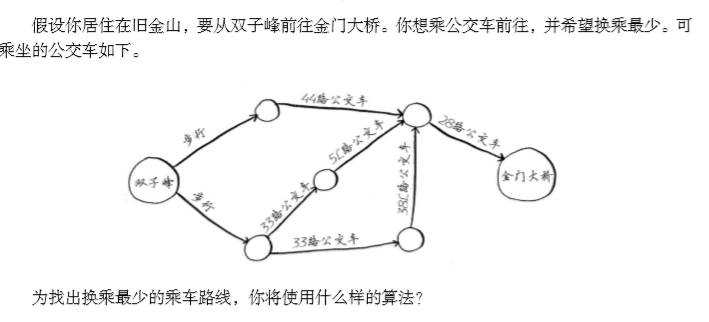
image.png

6.1 图简介

image.png
解决最短路径问题的算法被称为广度优先搜索。需要以下两步：

  1. 使用图建立问题模型。
  2. 使用广度优先搜索解决问题。

6.2 图是什么

图模拟一组连接

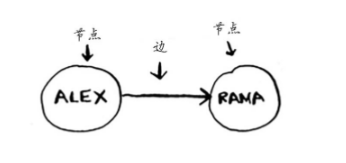
图由节点和有向边组成。根据有向边的含义不同，如下可以解释为：

  • ALEX 依赖于 RAMA 、ALEX 欠钱于 RAMA 。

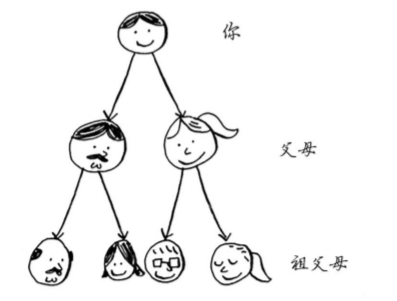
image.png

  • 树是一种特殊的图。

image.png

邻居

一个节点可能与众多节点直接相连，这些直接相连节点被称为邻居。 节点直接相连什么意思？

  • 对于无向图，两个相连的节点就是直接相连的，互为邻居。
    • image.png
  • 对于有向图，A到B直接相连，但B到A间接相连，所以B是A的邻居，但A不是B的邻居。
    • image.png

6.3 广度优先搜索

广度优先搜索是一种用于图的查找算法，可帮助 回答两类问题。

  • 第一类问题：从节点A出发，有前往节点B的路径吗？
  • 第二类问题：从节点A出发，前往节点B的哪条路径最短？

例如你需要找到一位芒果销售商，你使用一种算法来搜遍你的整个人际关系网，直到找到芒果销售商。这就是广度优先搜索算法。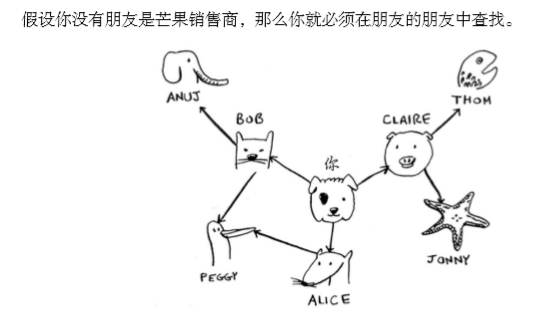
image.png

6.3.1 查找最短路径

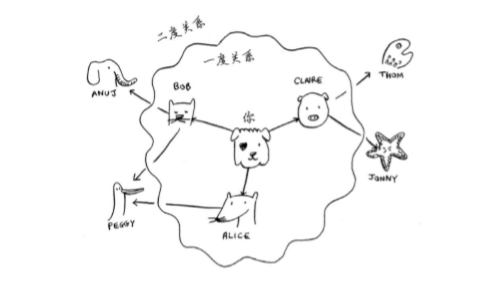
假如，朋友是一度关系，朋友的朋友是二度关系，以此类推。所以我们可以查找一度关系，再查二度关系，依次类推，便找到关系最近的供应商，也是找到最短路径。

  • 注意：需要按添加顺序进行检查。有一个可实现这种目的的数据结构，那就是队列（queue）。

image.png

6.3.2 队列

队列是一种先进先出（First In First Out，FIFO）的数据结构，而栈是一种后进先出（Last In First Out，LIFO）的数据结构。

6.4 实现图

用散列表去表示关系，例如，你和你的邻居们。

  • 注意有向图的关系是单向的，在下面的图中，你有三个邻居，但是其他人都没有邻居，因为他们并没有指向其他人。

image.pngimage.png

  1. # 注意这里映射的是一个数组
  2. graph = {} 
  3. graph["you"] = ["alice", "bob", "claire"]

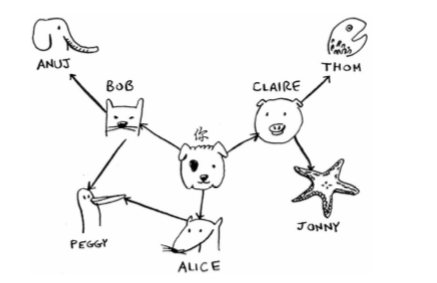
image.png

  • 将每个节点的键值对都添加到散列表，便得到了图的模型。
    • 注意1：这里是有向图，有邻居的节点才是键值，键-值对即是节点和节点的邻居们。
    • 注意2：散列表是无序的，因此添加键—值对的顺序无关紧要。

6.5 实现算法

算法基本原理

把等待检查的人都加入一个队列中，每次从队列中弹出一个人检查，如果检查成功则找到最短路径，如果检测失败则立即把他的所有朋友都压入到队列中，然后在循环上述。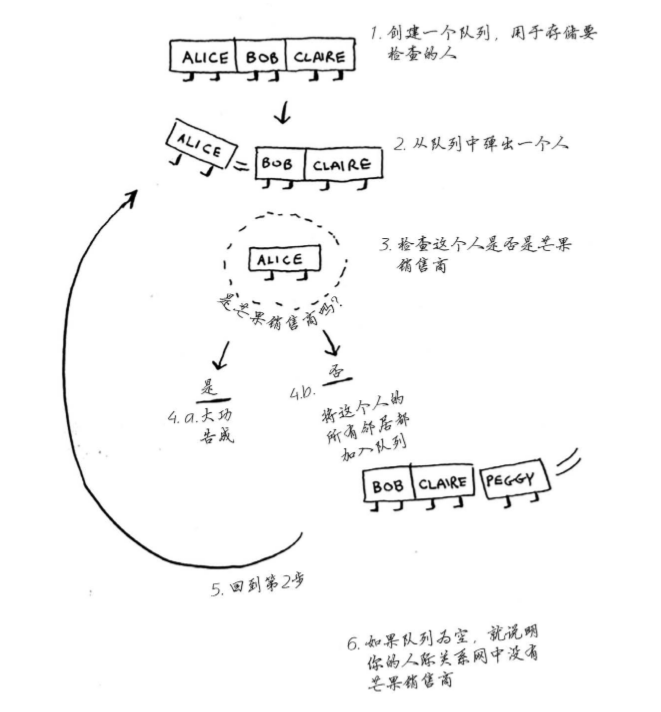
image.png

算法实现

  1. # 首先，创建一个双端队列
  2. from collections import deque
  3. search_deque = deque()   #<==============创建一个队列
  4. search_deque + = graph["you"]  #<========将你的邻居们压入，你的邻居们是一个数组。
  6. # 检查是否是供应商
  7. def person_is_seller(name):     
  8.     return name[-1] == 'mango' 
  10. while search_queue:       # <================只要队列不为空
  11.     person = search_queue.popleft()     #<======弹出队头的人检查
  12.     if person_is_seller(person):      #<======== 是供应商
  13.         print person + " is a mango seller!" 
  14.         return True                 
  15.     else: 
  16.         search_queue += graph[person]  #<======不是供应商，就将其朋友都压入队尾。
  17. return False          #<============进行到这里，说明没人是供应商。

改进广度优先搜索算法

  • 缺陷：如果C同时是A和B的朋友，那么第一，C将被检查两次，第二，这可能导致无限循环。
  • 改进：标记已经检查的人。
  1. from collections import deque
  2. def search(name):
  3.     search_deque = deque()
  4.     search_deque += gragh[name]
  5.     searched = []
  6.     while search_deque:
  7.         person = search_deque.popleft()
  8.         if not person in searched:
  9.             if person_is_seller(person):
  10.                 print person + 'is seller'
  11.                 return True
  12.             else:
  13.                 search_deque += gragh[person]
  14.                 searched.append(person)
  15. return False

运行时间

广度优先搜索的运行时间为 O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点（vertice）数，E为边数。

  • 解释：如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是 从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。 你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的， 即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。