本章内容

学习分而治之（divide and conquer，D&C）。
学习快速排序。快速排序采用分而治之策略。

小结

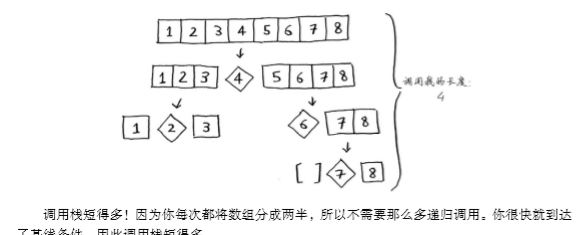
D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或只包含一个元素的数组。
实现快速排序时，请随机地选择用作基准值的元素。快速排序的平均运行时间为0(n log n)。
大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在。
比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O(n log n)的速度比O(n)快得多。

思考

4.1 分而治之

使用D&C策略！D&C算法是递归的。解决过程遵循下面两个步骤：

  1. 找出基线条件，这种条件必须尽可能简单。
  2. 不断将问题分解（或说缩小规模），直到符合基线条件。

    问题

    一个矩形足球场，如何均匀划分为方块，且方块尽可能大。

    前提知识：欧几里得算法求最大公约数

    image.png

解决

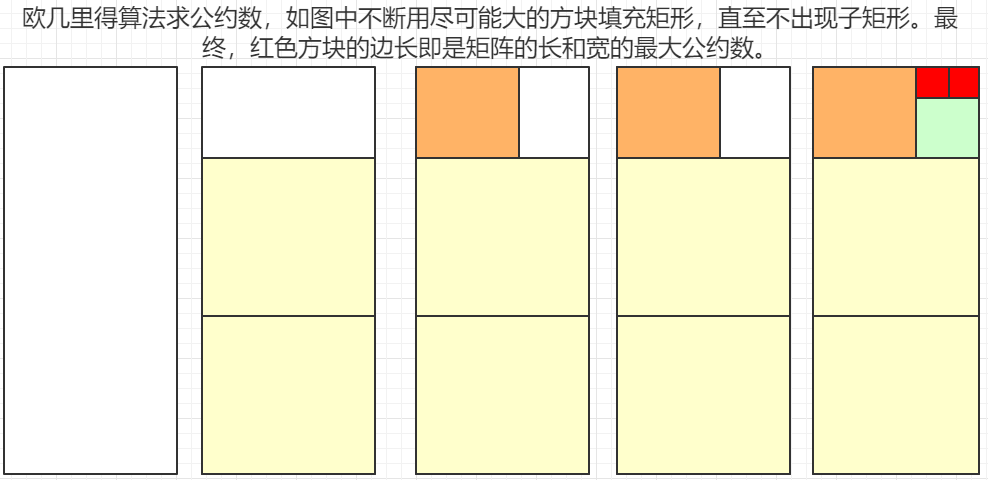
  • 基线条件可以是，某子矩形的一条边长是另一条边长的整数倍。该子矩形便可以划分出均匀的最大方块，这个方块，不仅适用于该子矩形，而且适用于整个足球场——因为，若C是A和B的公约数，那么(AB)%(CC) == 0，这里的A和B即为足球场的长和宽，C即为刚才提到的方块的边长。
  • 规模缩小可以是，不断划分出更小的子矩形，使其子矩形符合基线条件。

    提示

    涉及数组的递归函数时，基线条件通常是数组为空或数组只包含一个元素。

    函数式编程

    函数式编程常常使用递归。

    练习

    注意练习3和练习4
  1. # 练习1 数组元素之和
  2. def sum(list):
  3.     if list == []:
  4.         return 0;
  5.     else: 
  6.         return list[0]+sum(list[1:])
  9. # 练习2 编写一个递归函数来计算列表包含的元素数
  10. def count_(list):
  11.     if list == []:
  12.         return 0
  13.     else:
  14.         return (1+count_(list[1:]))
  16. # 练习3 找出列表中最大的数字
  17. def max(list):
  18.     if len(list) == 2:
  19.         return list[0] if list[0]>list[1] else list[1]
  20.     else:
  21.         sub_max = max(list[1:])
  22.         return list[0] if list[0]>sub_max else sub_max 
  24.     代码分析：1.基线条件是列表中只有两个元素 
  25.     2.递归条件是，将列表分为list[0]和list[1:]两个子列表，对于不符合基线条件的子列表再进行相同递归条件操作，
  26.     直至子列表符合基线条件，返回这两个子列表中的大者。可以看见需要需要执行递归条件的子列表的规模在不断缩小。
  28. # 练习4 分析二分查找中的分而治之
  29.     1.基线条件是数组中只含一个元素。如果查找值与这个元素匹配了，则找到了！否则，就说明它不在数组中
  30.     2.递归条件是，把数组分成两半，将其中一半丢弃，并对另一半二分查找。

4.2 快速排序

快速排序优于选择排序，C语言标准库中的函数qsqrt就是快速排序。快速排序使用了D&C。

  1. def quicksqrt(arr):
  2.     if len(arr) <= 1 :  
  3.         return arr     #<=====================================基准条件：为空或只有一个元素的数组是"有序"的
  4.     else:
  5.         pivot = arr[0] #<=====================================选择基准值pivot
  6.         less = [i for i in arr[1:] if i <= pivot]  #<========由所有【小于等于】基准值的元素组成的子数组
  7.         greater = [i for i in arr[1:] if i > pivot] #<=======由所有大于基准值的元素组成的子数组
  8.         return quicksqrt(less) + [pivot] + quicksqrt(greater) 
  10. print(quicksqrt([4,4,8,2,10]))

快速排序步骤如下：

  1. 选择基准值
  2. 以基准值为参照，将数组分成按元素的大小，分为：[小子数组]+[基准值]+[大子数组]
  3. 对2中的两个子数组，进行快速排序。

    图解

    待排序数组：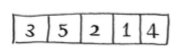
    image.png
    用3作为基准值：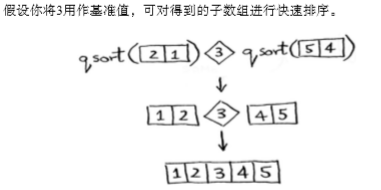
    image.png
    用5作为基准值：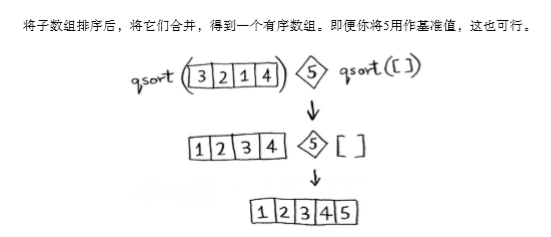
    image.png

    选取不同基准值的情况

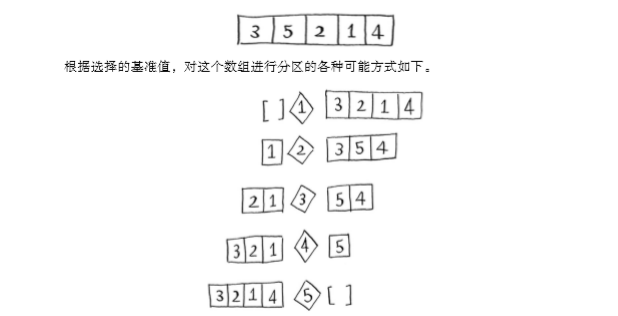
    image.png

4.3 大O表示法

image.png
快速排序的速度取决于选择的基准值。然而，归并排序的运行时间总是O(n log n)

  • 快速排序的平均速度O(n log n)，但最糟糕的情况下需要O(n)。

    4.3.2 快速排序的平均情况与最坏情况

    注意：快速排序无视数组是否已排序，这里的演示以有序数组为例。

    最坏情况：栈高度O(n) * 每层运行时间O(n) ,因此为O(n)

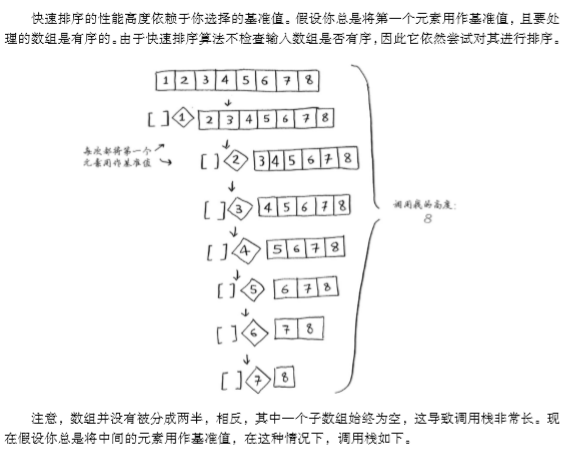
    image.png

最好情况：栈高度O(log n) * 每层时间O(n) ，因此为O(n log n)。

image.png