说明：本章内容太啰嗦了，建议直接看小结和7.5节的算法实现。

本章内容

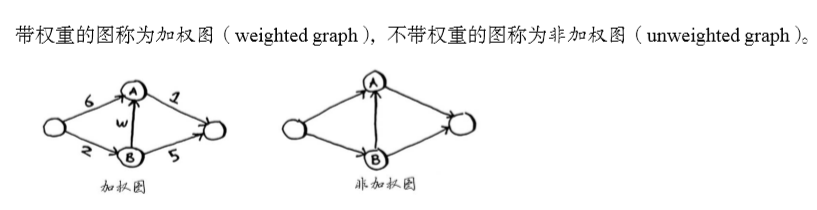
继续图的讨论，介绍加权图——提高或降低某些边的权重。
介绍狄克斯特拉算法，让你能够找出加权图中前往X的最短路径。
介绍图中的环，它导致狄克斯特拉算法不管用。

小结

广度优先搜索用于在非加权图中查找最短路径。
狄克斯特拉算法用于在加权图中查找最短路径。
仅当权重为正时狄克斯特拉算法才有用。
如果图中包含负权重，请使用贝尔曼-福德算法

7.1 使用狄克斯特拉算法

找出加权图中前往X的最短路。

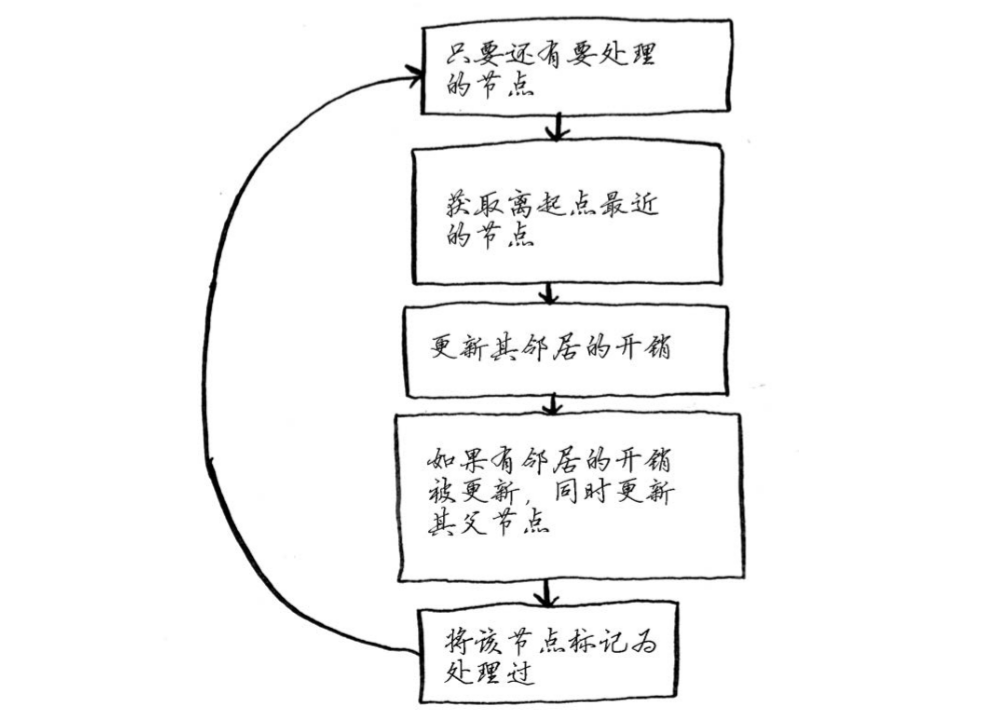
image.png

狄克斯特拉算法包含4个步骤

  1. 找出“最便宜”的节点，即可在最短时间内到达的节点。
  2. 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销
  3. 重复这个过程，直到对图中的每个节点都这样做了。
  4. 计算最终路径。
  • 实际的算法实现如下：（详见7.5实现部分）

image.png

距离向量算法？

如果你学过计算机网络的话，其中有一种路由算法，就是狄克斯特拉算法（Dijkstra）——距离向量算法。简单地说：我们需要利用每个节点到其邻居的代价，来不断地更新起点节点的”路由表”。

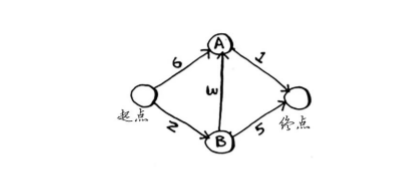
举个例子

image.png

第一步：找出最便宜的节点。

得到起点的表。知道最便宜的节点，即是B节点。
image.png

第二步：更新节点B的各个邻居的时间开销。

得到：起点—->B—>A 代价5。 起点—->B—->终点 代价5。更新起点的表。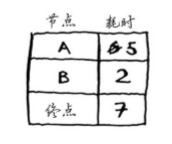
image.png

第三步：重复。

重复第一步：找出可在最短时间内前往的节点。你对节点B执行了第二步，除节点B外，可在最短时间内前往的节点是节点A。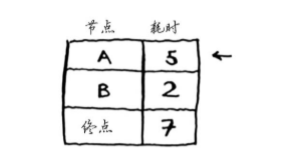
image.png
重复第二步：更新节点A的所有邻居的开销。
image.png

最后一步

计算最终路径将留到下一节去介绍，这里先直接将最终路径告诉你。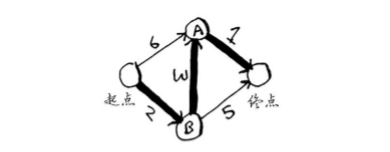
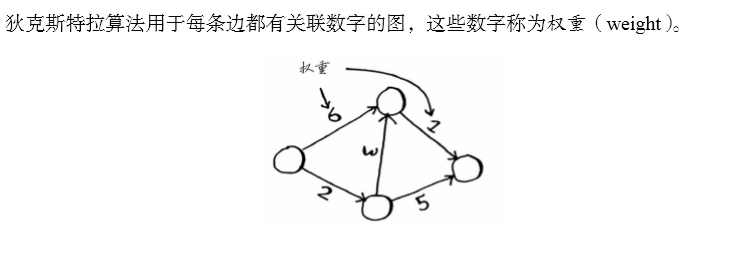
image.png

7.2 术语

权重

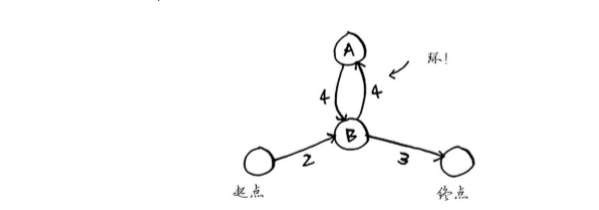
image.png

image.png

带环的加权图

image.png
在无向图中，每条边都是一个环。狄克斯特拉算法只适用于有向无环图（directed acyclic graph，DAG）。
无向图意味着两个节点彼此指向对方，其实就是环！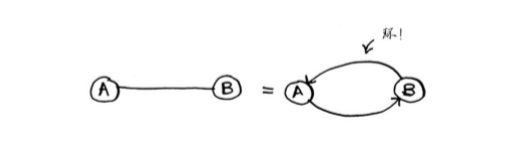
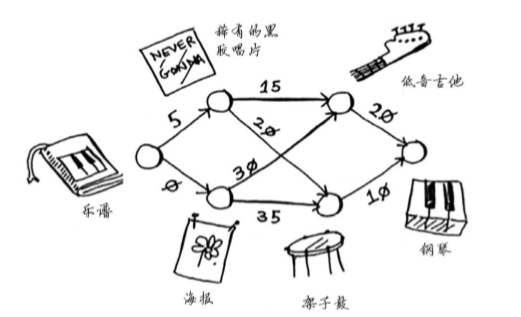
image.png

7.3 乐谱换钢琴

如下图，你现在拥有一本乐谱，你可以通过交换来最终换取钢琴，但是每个物品之间的交换代价是不同的。

image.png

准备工作

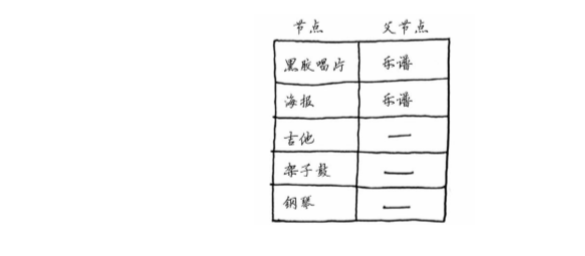
创建一个表格，在其中列出每个节点的开销。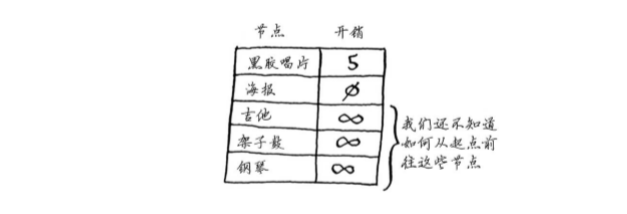
image.png
在执行狄克斯特拉算法的过程中，你将不断更新这个表。为计算最终路径，还需在这个表中 添加表示父节点的列。

image.png

第一步：找出最便宜的节点。

换海报需要支付的额外费用最少。

  • 这是狄克斯特拉算法背后的关键理念：找出图中最便宜的节点，并确保没有到该节点的更便宜的路径！

第二步：计算经过该节点前往其各个邻居的开销。

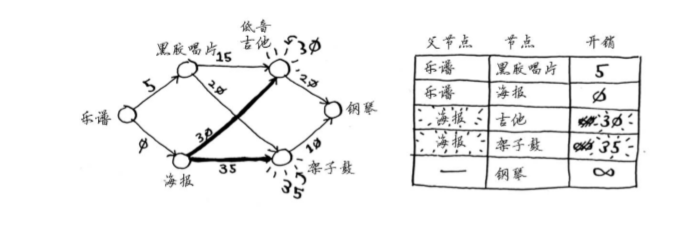
image.png
现在的表中包含低音吉他和架子鼓的开销。这些开销是用海报交换它们时需要支付的额外费用，因此父节点为海报。这意味着，要到达低音吉他，需要沿从海报出发的边前行，对架子鼓来说亦如此。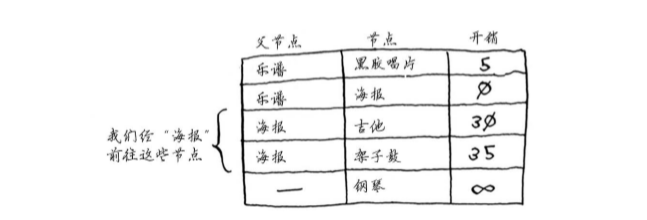
image.png

重复

再次执行第一步：下一个最便宜的节点是黑胶唱片——需要额外支付5美元。
再次执行第二步：更新黑胶唱片的各个邻居的开销。
image.png
你更新了架子鼓和吉他的开销！这意味着经“黑胶唱片”前往“架子鼓”和“吉他”的开销 更低，因此你将这些乐器的父节点改为黑胶唱片。
再次执行第一步：下一个最便宜的是吉他，因此更新其邻居的开销。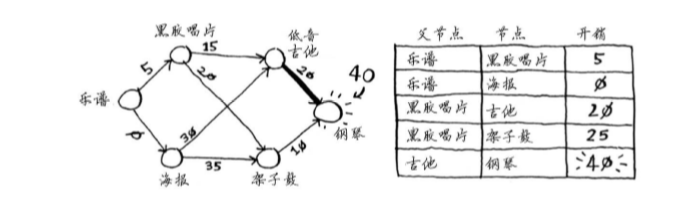
image.png
你终于计算出了用吉他换钢琴的开销，于是你将其父节点设置为吉他。最后，对最后一个节 点——架子鼓，做同样的处理。
image.png
如果用架子鼓换钢琴，Rama需要额外支付的费用更少。因此，采用最便宜的交换路径时， Rama需要额外支付35美元。

计算最终路径

现在来兑现前面的承诺，确定最终的路径。当前，我们知道最短路径的开销为35美元，但如 何确定这条路径呢？为此，先找出钢琴的父节点——架子鼓，再找出架子鼓的父节点——黑胶唱片，再出黑胶唱片的父节点——乐谱。
image.png

7.4 负权边

先说结论：不能将狄克斯特拉算法用于包含负权边的图。在包含负权边的图中，要找出最短路径，可使用另一种算法——贝尔曼-福德算法（Bellman-Ford algorithm）

  • 这是因为狄克斯特拉算法这样假设：该算法认为空权比负权最便宜，所以选择错了最便宜节点，并且认为对于处理过的最便宜节点，没有前往该节点的更短路径。 这种假设仅在没有负权边时才成立

7.5 代码实现

image.png

准备工作，建立模型

要编写解决这个问题的代码，需要三个散列表。 随着算法的进行，你将不断更新散列表costs和parents。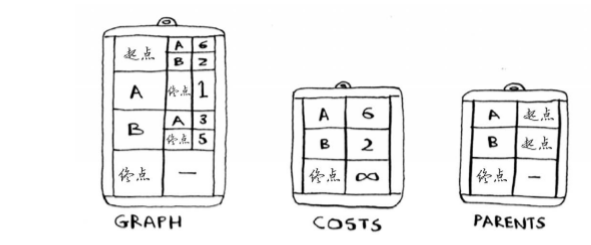
image.png

第一个表，graph散列表。

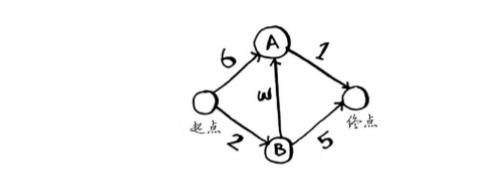
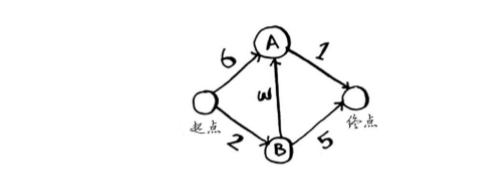
存储节点的所有邻居，建立图模型。为了在图模型中表示这些边的权重，还需要使用另一个散列表。简单说，图模型的散列表是长这样的：
graph = { ‘start’ : { ‘a’ : 6 , ‘b’ : 2 } , ‘a’ : { ‘fin’ : 1 } , ‘b’ : { ‘a’ : 3 , ‘fin’ : 5 } ，’fin’ : { } } 。
image.png

  1. # 创建图
  2. graph = {} 
  4. # start节点及其邻居们
  5. graph['start'] = {}
  6. graph['start']['a'] = 6
  7. graph['start']['b'] = 2
  9. # a节点及其邻居们
  10. graph['a'] = {}
  11. graph[a]['fin'] = 1
  13. # b节点及其邻居们
  14. graph['b'] = {}
  15. graph[b]['a'] = 3
  16. graph[b]['fin'] = 5
  18. # 终点没有任何邻居
  19. graph['fin'] = {}

第二个表，cost散列表。

存储从起点到其他节点的开销。未知开销被设为无限大，python的表示：infinity = float(‘inf’)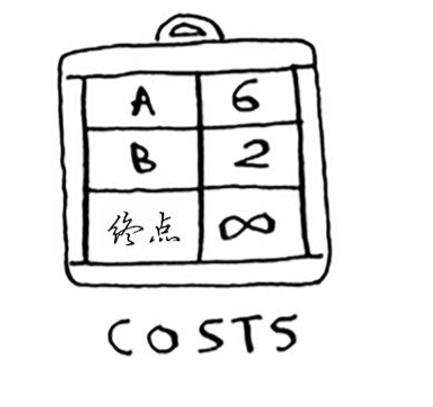
image.png

  1. # cost散列表
  2. infinity = float('inf')
  3. costs = {}
  4. costs['a'] = 6
  5. cost['b'] = 2
  6. cost['fin'] = infinity

第三个表，parents散列表。

用于存储父节点。没有父节点，则设置为None。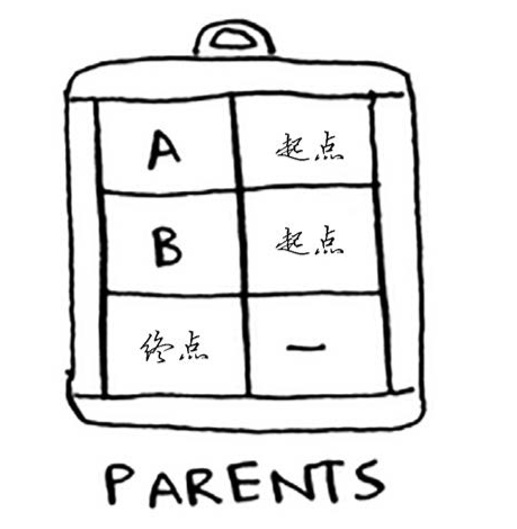
image.png

  1. # parents散列表
  2. parents = {}
  3. parents['a'] = 'start'
  4. parents['b'] = 'start'
  5. parents['fin'] = None

最后，需要一个数组用于记录

记录处理过的节点，因为在Dijkstra算法中，对于同一个节点，只需要处理一次。

  1. processed = {}

Dijkstra算法实现

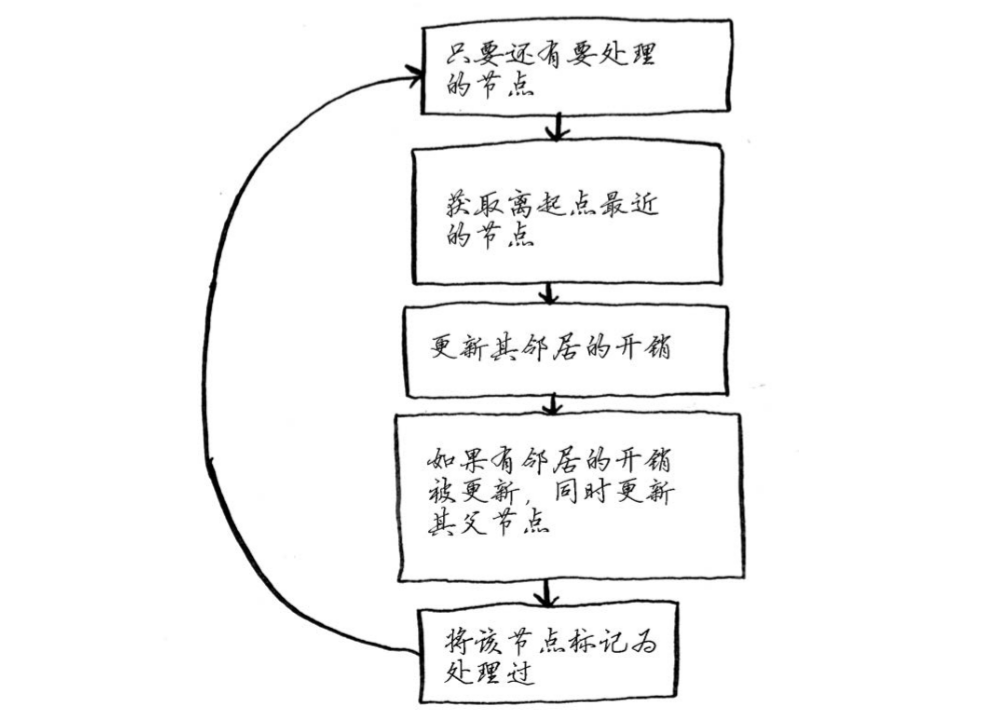
image.png

完整代码

1.建立图模型

  1. ### 创建图
  2. graph = {} 
  3. # start节点及其邻居们
  4. graph['start'] = {}
  5. graph['start']['a'] = 6
  6. graph['start']['b'] = 2
  7. # a节点及其邻居们
  8. graph['a'] = {}
  9. graph['a']['fin'] = 1
  10. # b节点及其邻居们
  11. graph['b'] = {}
  12. graph['b']['a'] = 3
  13. graph['b']['fin'] = 5
  14. # 终点没有任何邻居
  15. graph['fin'] = {}
  17. ### cost散列表
  18. infinity = float('inf')
  19. costs = {}
  20. costs['a'] = 6
  21. costs['b'] = 2
  22. costs['fin'] = infinity
  24. ### parents散列表
  25. parents = {}
  26. parents['a'] = 'start'
  27. parents['b'] = 'start'
  28. parents['fin'] = None
  29. parents['start'] = None

2.算法实现

  1. ### 已处理列表
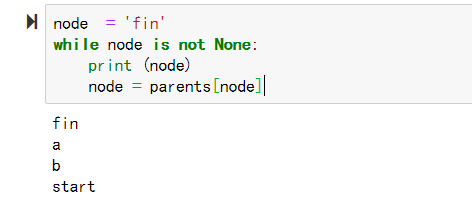
  2. processed = []
  4. ### 首先，找出未处理且开销最低的节点的函数
  5. def find_lowest_cost_node(costs):
  6.     lowest_cost = float('inf')
  7.     lowest_cost_node = None
  8.     for node in costs:        # 遍历所有节点,找出没有被处理过，且开销最低的节点
  9.         cost = costs[node]
  10.         if node not in processed and cost < lowest_cost:  
  11.             lowest_cost = cost
  12.             lowest_cost_node = node
  13.     return lowest_cost_node
  15. ### 更新节点邻居
  16. node  = find_lowest_cost_node(costs)
  17. while node is not None:  #<=====while循环在所有节点都被处理后结束
  18.     cost = costs[node]
  19.     neighbors = graph[node]  
  20.     for n in neighbors.keys():   #<=====遍历当前节点的邻居
  21.         new_cost = cost + neighbors[n]
  22.         if new_cost < costs[n]: #<=======如果经过当前节点到其邻居的代价更小，
  23.             costs[n] = new_cost #<======就更新该邻居的开销
  24.             parents[n] = node #<======同时将该邻居的节点更新为当前节点
  25.     processed.append(node)  #<=======将当前节点放入已处理列表
  26.     node  = find_lowest_cost_node(costs)   #<===找出接下来要处理的节点，并循环

3.测试输出，得到代价路径为 start -> b -> a -> fin
image.png