编码与调制

在计算机网络中

1. 计算机需要处理和传输用户的文字、图片、音频和视频。统称为消息
2. 数据是运送消息的实体。人类比较熟悉的是十进制数据，而计算机只能处理二进制数据（0/1）
3. 计算机中的网卡将0/1变换成相应的电信号发送到网线。也就是说，信号是数据的电磁表现
4. 由信源发出的原始电信号，称为基带信号。基带信号又可分为两类
   1. 数字基带信号。例如，计算机内部CPU与内存之间的传输信号
   2. 模拟基带信号。例如，麦克风收到声音后产生的音频信号
5. 信号需要在信道中进行传输。信道可分为数字信道和模拟信道两种

编码

• 在不改变信号性质的前提下，仅对数字基带信号的波形进行交换，称为编码
• 编码后产生的信号仍为数字信号，可以在数字信道中传输。例如，以太网使用曼彻斯特编码、4B/5B、8B/10B等编码

调制：

• 把数字基带信号的频率范围，搬移到较高的频段，并转换为模拟信号，称为调制。
• 调制后产生的信号是模拟信号，可以在模拟信道中传输。例如，WIFI使用补码键控、直接序列扩频、正交频分复用等调制方法

对于模拟基带信号的处理，也有编码和调制两种方法

• PCM：将模拟音频信号，通过采样、量化、编码这三个步骤进行数字化
• 模拟基带信号调制，例如传统电话

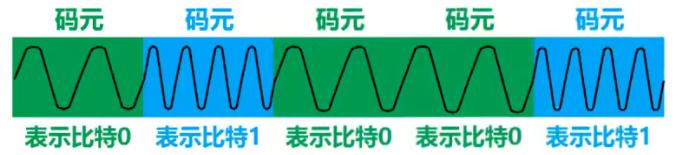
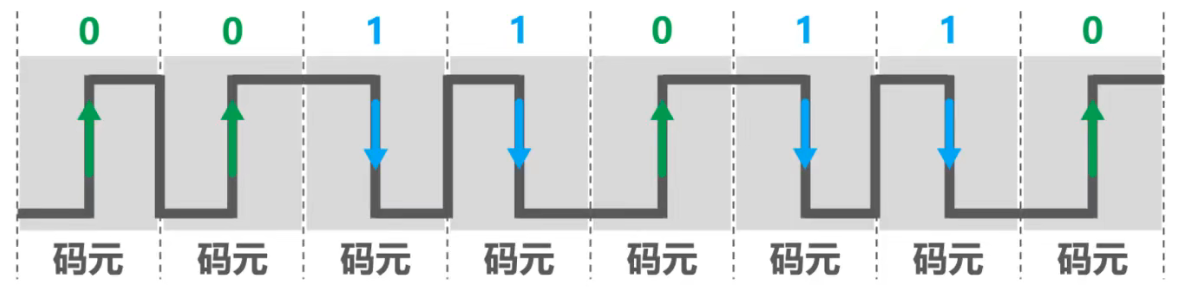
码元

在使用时间域的波形表示数字信号时，代码不同离散数值的基本波形称为码元

• 简单来说，码元就是构成信号的一段波形
• 比如，图中第一段波形是构成该信号的一个基本波形，我们可称其为码元，它可以表示比特0。可见此图的信号由两种码元构成

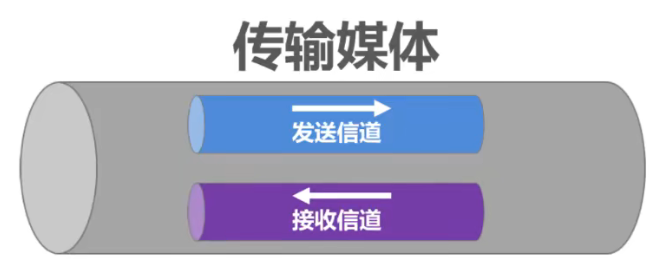
传输媒体与信道的关系

严格来说，传输媒体和信道不能直接划等号

1. 对于单工传输，传输媒体中只包含一个信道。要么是发送信道，要么是接收信道
2. 而对于半双工和全双工传输，传输媒体中要包含两个信道。一个是发送信道，另一个是接收信道
3. 如果使用信道复用技术，一条传输媒体还可以包含多个信道

在计算机网络中，常见的是将数字基带信号通过编码或调制的方法在相应信道进行传输。

常用编码

不归零编码（存在同步问题）

所谓不归零，就是指在整个码元时间内，电平不会出现零电平。一个码元的所有时间内都是正电平或低电平

问题：接收端如何判断出某个时间内是2个码元，还是3个码元？

• 这需要发送方的发送与接收方的接收做到严格的同步。这就需要额外一根传输线来传输时钟信号
• 接收方按照时钟信号的节拍来逐个接收码元

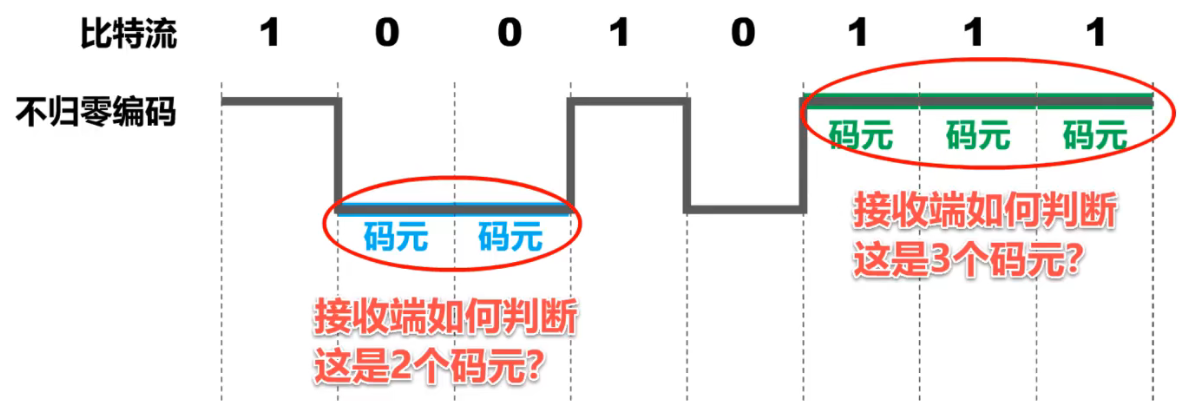
然而，对于计算机网络，宁愿用这根传输线来传输数据信号，而不是传输时钟信号。因此，由于不归零编码存在同步的问题，计算机网络中的数据传输不采用这类编码

归零编码（自同步，编码效率低）

每个码元传输结束后，信号都要“归零”。所以，接收方只要在信号归零后进行采样即可。不需要单独的时钟信号

• 实际上，归零编码相当于把时钟信号用“归零”方式编码在了数据之内，这称为“自同步”信号

但是，归零编码中大部分的数据带宽，都用来传输“归零”而浪费掉了。

曼彻斯特编码

在每个码元时间的中间时刻，信号都会发生跳变

• 例如，负跳变表示比特1，正跳变表示比特0
• 码元中间时刻的跳变既表示时钟，又表示数据
• 传统以太网（10Mb/s）使用的就是曼彻斯特编码

差分曼彻斯特编码

在每个码元时间的中间时刻，信号都会发生跳变。

• 与曼特斯特编码不同，跳变仅表示时钟。
• 码元开始处电平是否发生变化，来表示0或1
• 比曼特斯特编码变化少，更适合较高的传输速率

习题

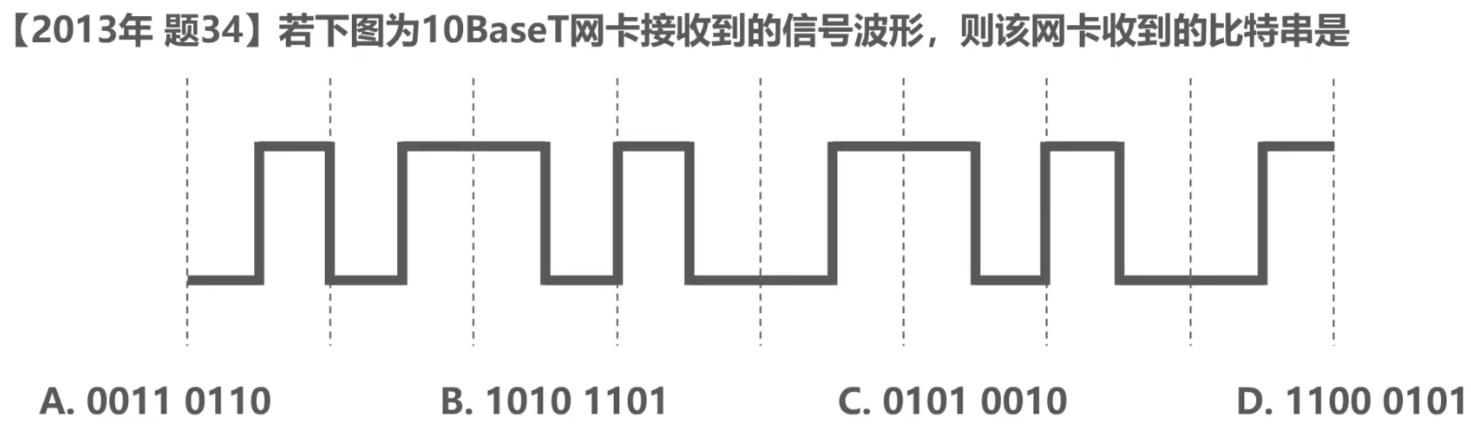
解析

• 10表示10Mb/s；Base表示基带传输；T表示双绞线。这种以太网使用曼彻斯特编码
• 每个码元在中间时刻跳变，按此特点找出每个码元

• 正跳变表示1，还是表示0，可自行假设。然后看有没有选项

  

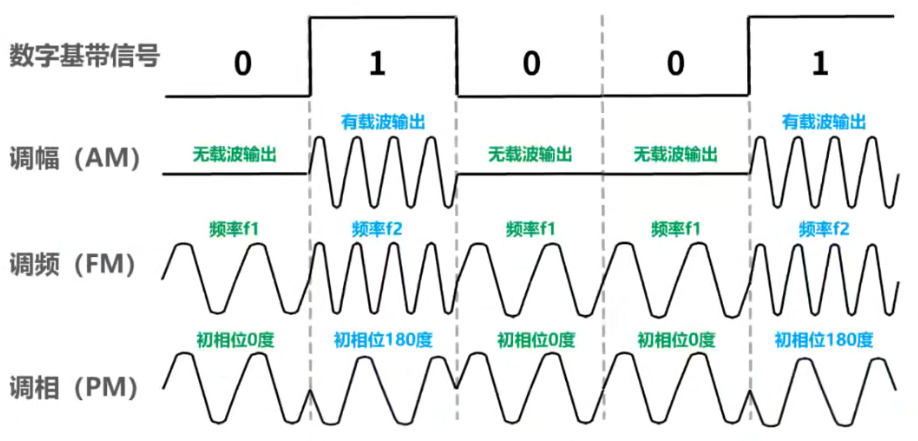
调制方法

基本调制方法

一个数字基带信号，来自信源的原始数字信号，我们要使用模拟信道来传输，因此需要将数字基带信号通过调制方法，调制成可以在模拟信道中传输的模拟信号。

• 第二图像是调幅所产生的模拟信号
• 第三幅是调频所产生的模拟信号
• 第四幅是调相所产生的模拟信号

混合调制

使用基本调制方法，1个码元只能包含1个比特信息。如何能使1个码元包含更多比特呢？

• 可以采用混合调制的方法

模拟信号有三种元素：频率、相位、振幅

• 因为频率是相位随时间的变化率，即频率和相位是相关的。所以用频率和相位混合没有用，还是只有一个变量。因此，一次只能调制频率和相位两个中的一个
• 通常情况下，相位和振幅可以结合起来一起调制，称为正交振幅调制QAM

举例，属于QAM的QAM-16

• 这种调制方法所调制出来的波形可以有12种相位
• 每种相位有1或2种振幅可选

定义一个二维直角坐标系，根据下列定义将码元画在图中。此图，称之为星座图

• 振幅：点与圆心连线的距离
• 相位：连线与横坐标的夹角

使用此方法，可将QAM16可调制出的16种码元，都绘制到此星座图上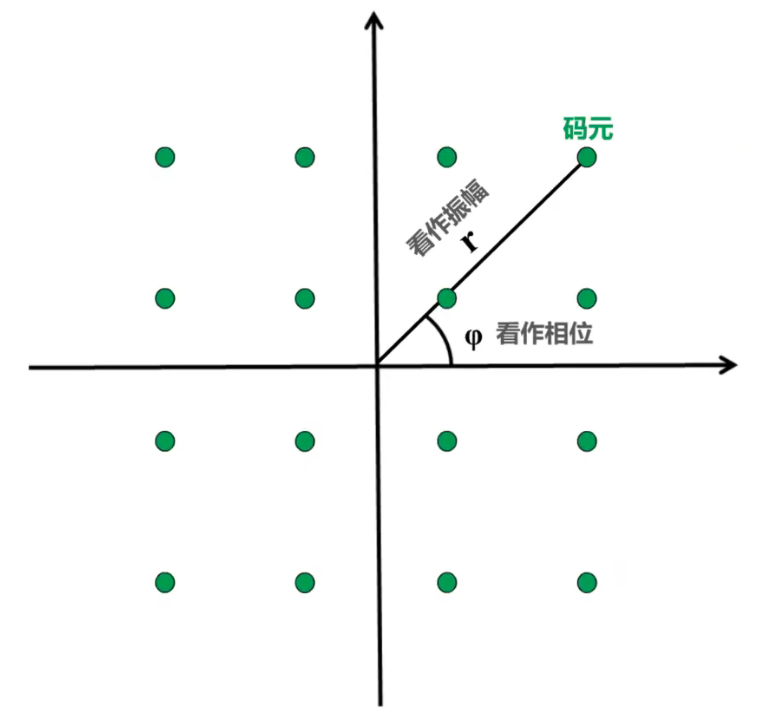

每个码元可以包含几个比特？

• 可以调制出16种码元（波形），每种码元可对应表示4个比特
• 因为16是2的4次方，一个比特可以有1/0两种，4个比特就有222*2=16种
• 四个二进制数可以表示16种情况，刚好对应这16个码元

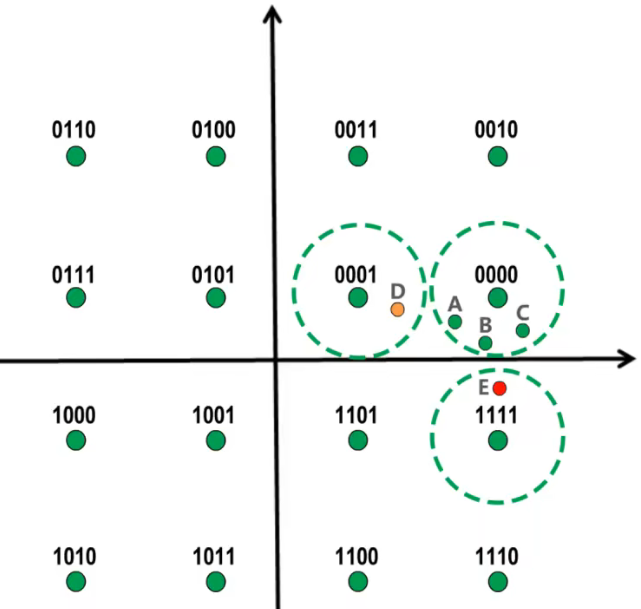
每个码元与4个比特的对应关系可以随便定义吗？

• 如图所示，我们随便定义每个码元所对应的4个比特
• 假设ABCDE是接收端收到的5个码元
  • 在发送端，这5个码元都是0000（即4个比特0）
  • 但是由于传输过程中产生失真，我们将接收到的模拟信号根据星座图的定义，绘制在图中
  • 发现，它们在星座图中并未落在理想位置（即0000上）
• 接收端根据最近原则，将这5个码元进行解调
  • A、B、C解调为0000。这和发送时是一样的，即这三个码元解调正确
  • D被解调为0001。但发送端发送的是0000，这其实错误了，有1个错位了
  • 将E解调为1111。但发送端发送的是0000。4位全错了
• 这就说明，每个码元与4个比特的对应关系不能随便定义。就是为了防止信号的失真导致的错误

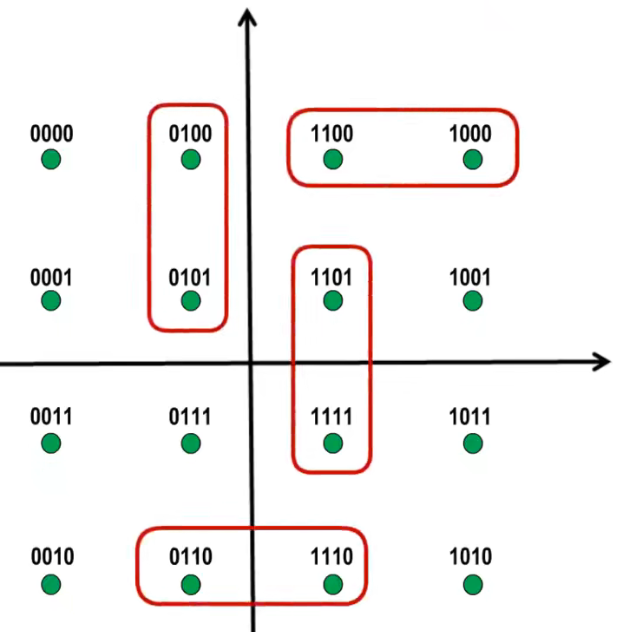
每个码元与4个比特的对应关系采用格雷码

• 也就是任意两个相邻码元只有1个比特不同
• 这样就把信号的失真导致的影响，降到了一个比特。也就是说，现在最多就错一位，原来的方法最多4位全错！