B+索引在数据库中有一个特点是高扇出性，因此在数据库中，B+树的高度一般都在2~4层，这也就是说查找某一键值的行记录时最多只需要2到4次IO。

插入

B+树的插入必须保证插人后叶子节点中的记录依然排序，同时需要考虑插人到B+树的三种情况，每种情况都可能会导致不同的插入算法。

Leaf Page满 Index Page满 操作
No No 直接将记录插入到叶子节点
Yes No
1. 拆分 Leaf Page
1. 将中间的节点放入到 Index Page中
1. 小于中间节点的记录放在左边
1. 大于或等于中间节点的记录放右边
Yes Yes
1. 拆分 Leaf Page
1. 小于中间节点的记录放左边
1. 大于或等于中间节点的记录放右边
1. 拆分 Index Page
1. 小于中间节点的记录放左边
1. 大于中间节点的记录放右边
1. 中间节点放入上一层 Index Page

基础B+数图
MySQL B+树-初始状态.png
用户插入 28 这个键值，发现当前 Leaf Page 和 Index Page 都没有满，直接进行插入。
结果如图：
MySQL B+树-插入28.png
接着再插入70这个键值，这时原来的 Leaf Page 已经满了，但是 Index Page 还没有满，此时插入 Leaf Page后的情况为，50/55/60/65/70，并根据中间的值 60 来拆分叶子节点。
结果如图
MySQL B+树-插入70.png
最后插入键值95，这时Leaf Page 和 Index Page都满了，这时需要做两次拆分。
先根据75/80/85/90/95的中间值85进行拆分Leaf Page，75/80 作为一个Leaf Page，85/90/95作为一个Leaf Page；
再根据25/50/60/75/85的中间值60进行拆分Index Page，25/50作为一个中间的Index Page，60单独作为一个Index Page，75/85作为一个中间的Index Page。
结果如图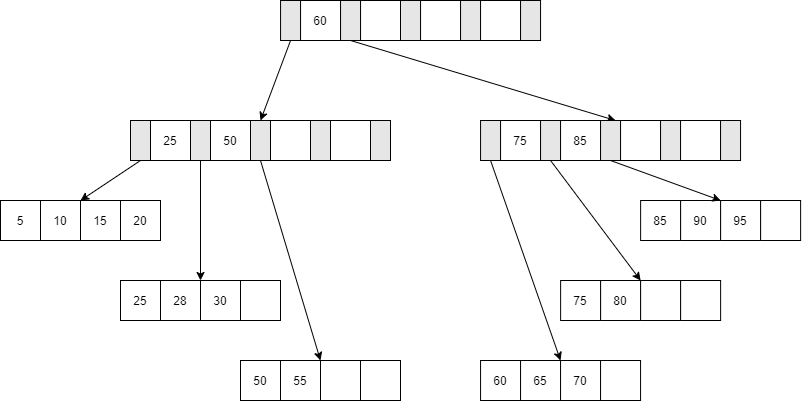
MySQL B+树-插入95.png

旋转插入

不管怎么变化，B+树总会保持平衡。但是为了保持平衡对于新插入的键值可能需要做大量的拆分页操作。因为B+树结构主要用于磁盘，页的拆分意味着磁盘的操作，所以应该在可能的情况下尽量减少页的拆分操作。因此，B+树同样提供了类似于平衡二叉树的旋转功能。
旋转发生在 Leaf Page 已经满，但是其他左右兄弟节点没有满的情况下。此时B+树不会急于去做拆分页的操作，而是将记录所在页的兄弟节点上。
例如，若插入键值70，其实B+树并不会急于拆分叶子节点，而是做旋转操作。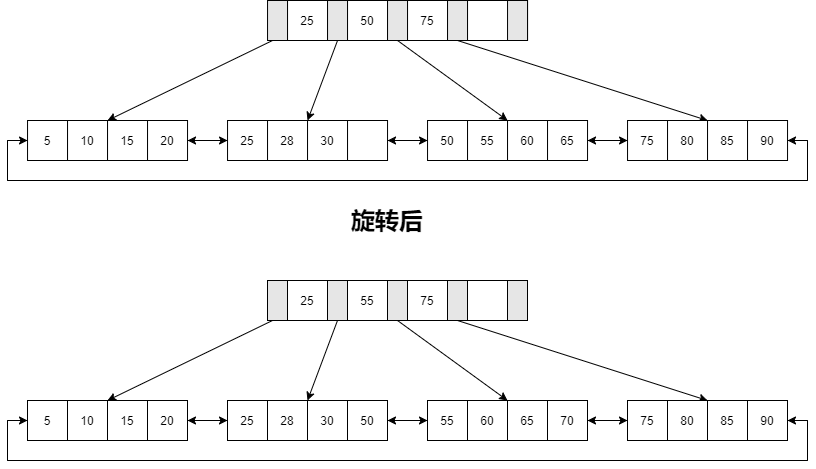
MySQL B+树-旋转插入70.png

删除

B+树使用填充因子（fillfactor）来控制树的删除变化，50%是填充因子可设的最小值。B+树的删除操作同样必须保证删除后叶子节点中的记录依然排序，同插人一样，B+树的删除操作同样需要考虑三种情况，与插入不同的是，删除根据填充因子的变化来衡量。
B+树使用填充因子来控制页面的分裂和合并，设置数据占用页面空间的百分比，目的是为后面的数据预留一部分页空间，当有新数据时，可以放到预留的页空间中，避免分页的发生。

叶子节点小于填充因子 中间节点小于填充因子 操作
No No 直接将记录从叶子节点上删除，如果该节点还是Index Page的节点，用该节点的有节点代替
Yes No
1. 合并叶子节点和他的兄弟节点
1. 同时更新 Index Page
Yes Yes
1. 合并叶子节点和他的兄弟节点
1. 更新 Index Page
1. 合并 Index Page 和他的兄弟节点

删除键值70，60/65/70 这一叶子节点，删除后70后，填充因子为50%，中间节点75/85不受影响，填充因子保持50%没有变化，直接删除即可。
结果如图：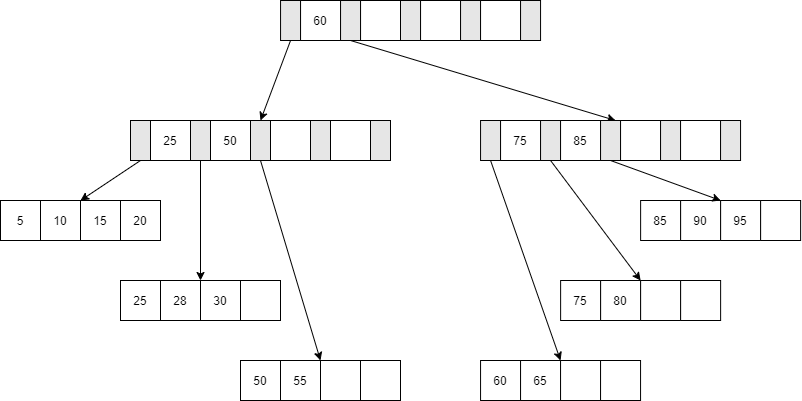
MySQL B+树-删除70.png
接着删除键值25，在Leaf Page上25/28/30，删除25后，填充因子为50%，同时25也是中间节点，所以需要将25删除后，再将右边的28代替Index Page原来25的位置。
结果如图：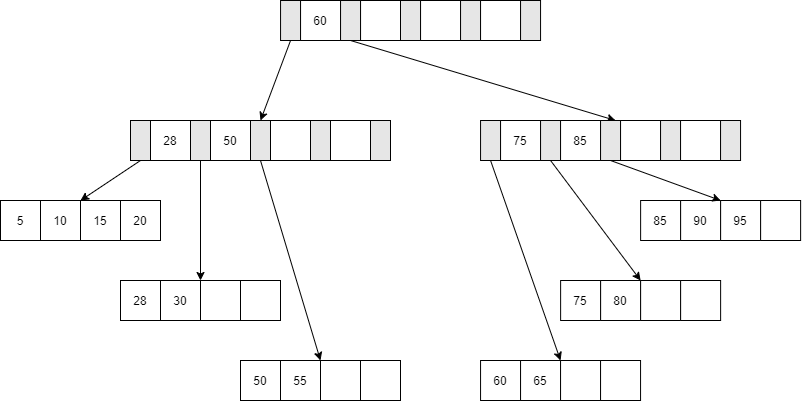
MySQL B+树-删除25.png
最后删除键值60，删除键值为60的记录后，60/65的填充因子为25%，小于50%，此时需要合并其他兄弟节点，同样60还在Index Page 上，删除60后，60所在的Index Page 填充因子为0%，小于50%，所以也需要Index Page 做合并操作。
MySQL B+树-删除60.png