Lecture 1 : How to achieve high-performance?

• Multicore: factor 4• Superscalar: factor 2• Pipelining: factor 4• Vectorization: factor 8

Clock Speed

Clock Speed of the CPU: the number of clock cycles per second

The total latency of the instruction (roughly speaking, the time it takes to launch multiplication to the time when the result is available) has dropped significantly over the years: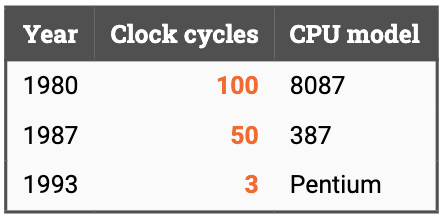

The joint effect of increasing clock speeds and decreasing instruction latencies implied massive improvements in the performance. In just a couple of decades, the time it took to complete a floating point multiplication decreased several orders of magnitude, from tens of microseconds to tens of nanoseconds.

After 2000

Clock Speeds stopped improving. The clock speed of a modern computer is almost always somewhere in the ballpark of 2–3 GHz.

Since 2000, the number of transistors in a state-of-the-art CPU has increased by more than two orders of magnitude, but this is not visible in the performance if we look at the time it takes to complete a single instruction. A single floating point multiplication took roughly 2 nanoseconds in 2000, and it still takes roughly 2 nanoseconds today.

• Latency: time to perform an operation from start to finish.
• Throughput: how many operations are completed per time unit, in the long run.

Modern CPUs do exactly the same thing as our university: they are able to keep several instructions in execution simultaneously, and hence they can obtain a much higher throughput than what one would expect based on the instruction latency.

Pipelining

Each arithmetic unit typically has a throughput of 1 operation per clock cycle, and modern CPUs have a large number of parallel arithmetic units. For example, in a typical modern CPU there are 16 parallel units for single-precision floating point multiplications per core. Hence a modern 4-core CPU can do floating point multiplications at a throughput of 64 operations per clock cycle, or roughly 200 billion operations per second (recall that the clock speed is typically around 3 GHz, i.e., 3 billion clock cycles per second).

This is a dramatic improvement in comparison with the CPUs from the 1990s, in which the throughput of floating point multiplications was typically in the ballpark of 0.5 operations per clock cycle.

the latency of individual operations is not improving at all, only throughput is improving. And to benefit from the new kind of performance, we will need new kind of software that explicitly takes into account the difference between throughput and latency.

How to exploit parallelism?

independent operations

we need to have independent operations in our program.
Dependent operations: The entire sequence of operations is inherently sequential. Even if we had a large number of parallel multiplication units available, we could not use more than one at the same time. Pipelining would not help, either; we cannot start an operation until we know the values of the operands.

Independent operations: There are lots of opportunities for parallelism in this code, and the only fundamental limitation for the performance is the throughput of multiplications.

Instruction-level parallelism

Instruction-level parallelism is automatic

Main Idea:
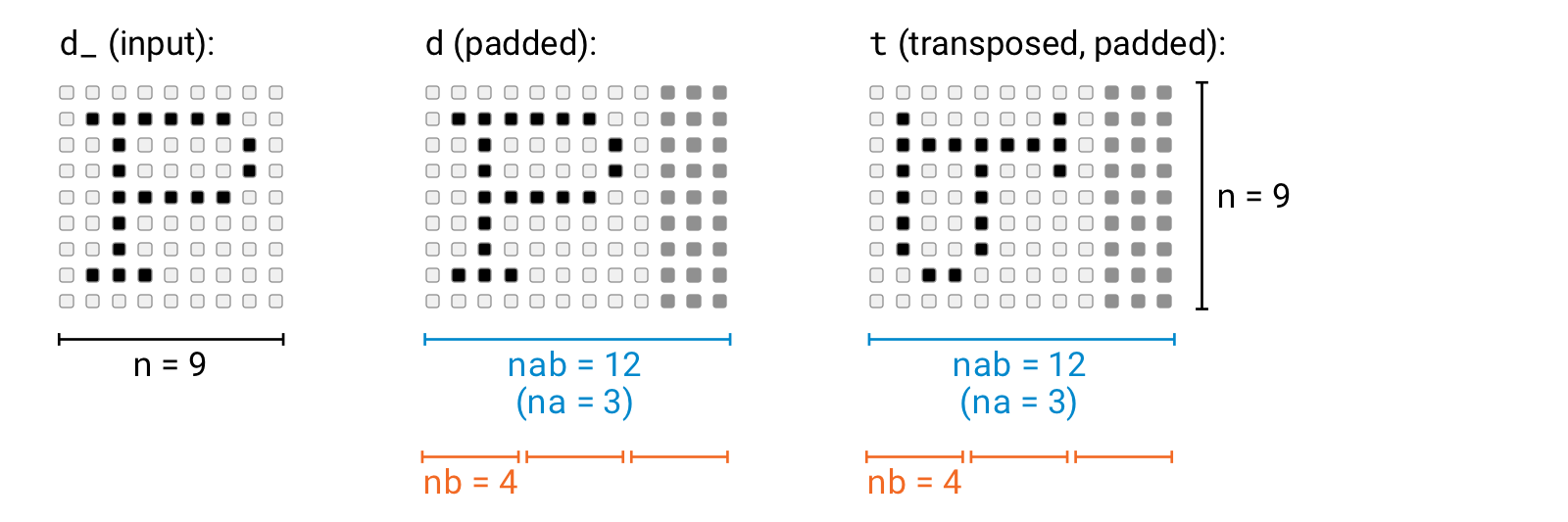
Preprocess the data so that we add some padding elements so that the width of the array is a multiple of 4.

constexpr int nb = 4;
int na = (n + nb - 1) / nb;
int nab = na*nb;
    constexpr float infty = std::numeric_limits<float>::infinity();
    //copy the value
    #pragma omp parallel for
    for (int j = 0; j < n; ++j) {
        for (int i = 0; i < n; ++i) {
            d[nab*j + i] = d_[n*j + i];
            t[nab*j + i] = d_[n*i + j];
        }
    }
    #pragma omp parallel for
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            // vv[0] = result for k = 0, 4, 8, ...
            // vv[1] = result for k = 1, 5, 9, ...
            // vv[2] = result for k = 2, 6, 10, ...
            // vv[3] = result for k = 3, 7, 11, ...
            float vv[nb];
            for (int kb = 0; kb < nb; ++kb) {
                vv[kb] = infty;
            }
            for (int ka = 0; ka < na; ++ka) {
                for (int kb = 0; kb < nb; ++kb) {
                    float x = d[nab*i + ka * nb + kb];
                    float y = t[nab*j + ka * nb + kb];
                    float z = x + y;
                    vv[kb] = std::min(vv[kb], z);
                }
            }
            // v = result for k = 0, 1, 2, ...
            float v = infty;
            for (int kb = 0; kb < nb; ++kb) {
                v = std::min(vv[kb], v);
            }
            r[n*i + j] = v;
        }
    }

superscalar processor

in each clock cycle, we can launch more than one instruction. With one thread, we are now doing 1.6 useful operations per clock cycle.