赫夫曼编码是赫夫曼树在电讯通信中的经典应用之一。
广泛地用于数据文件压缩。其压缩率通常在20%～90%之间。
赫夫曼编码是可变长编码（VLC）的一种。
赫夫曼编码压缩数据，是无损压缩。

原理剖析

定长编码

比如下面的字符串：

i like like like java do you like a java

一共有40个字符（包括标点符号和空格）

计算机中的信息最终都会转换成01二进制，上面的字符串最终转换成二进制如下

01101001001000000110110001101001011010110110010100100000011011000110100101101011011001010010000001101100011010010110101101100101001000000110101001100001011101100110000100100000011001000110111100100000011110010110111101110101001000000110110001101001011010110110010100100000011000010010000001101010011000010111011001100001

上面的二进制可以参考下图，不足8位的在前面补0，8位一字节，就是上面字符串的一个字符。
转换成二进制后，二进制的长度是320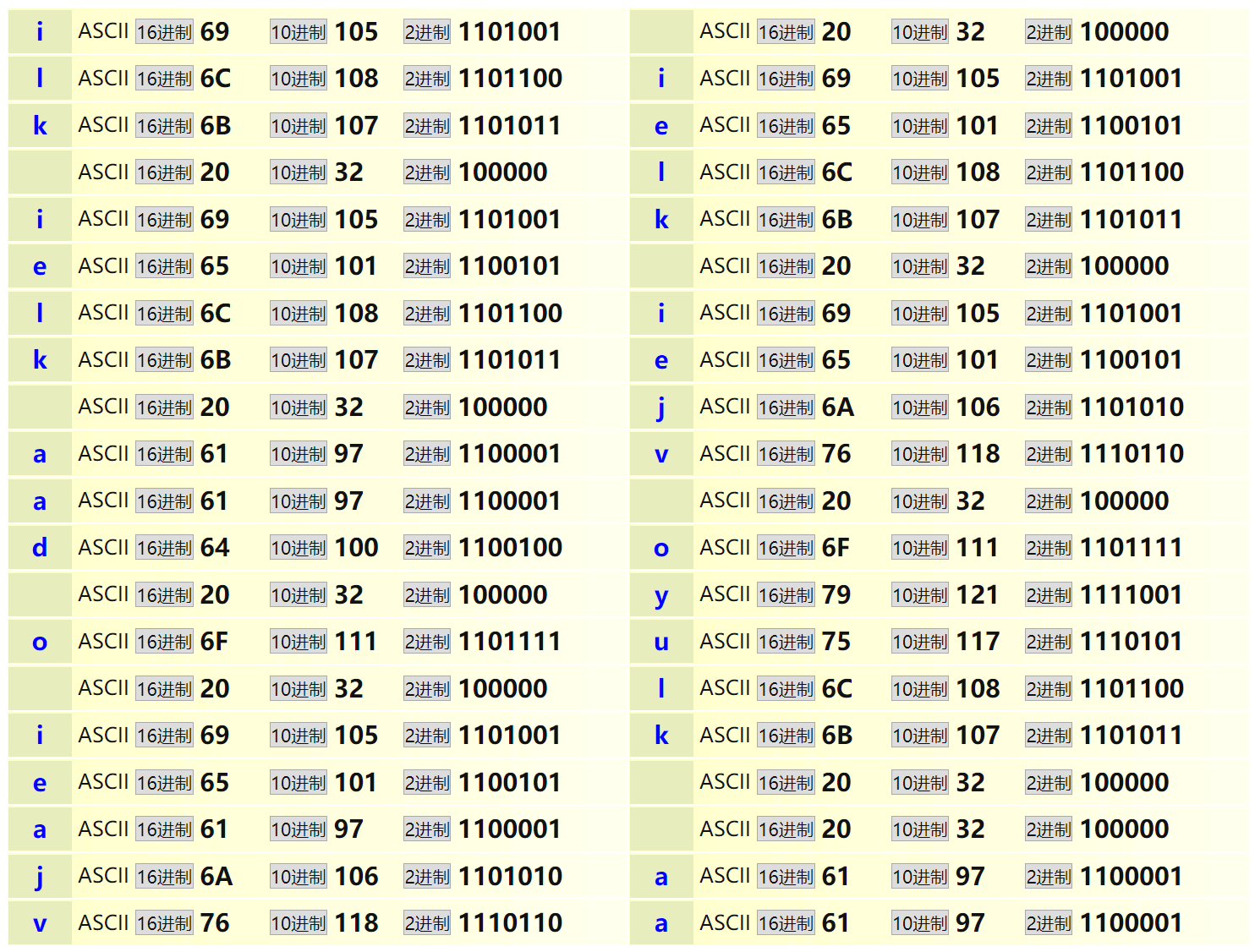
image.png

变长编码

i like like like java do you like a java

  1. 统计每个字符对应的个数
    • d：1
    • y：1
    • u：1
    • j：2
    • v：2
    • o：2
    • l：4
    • e：4
    • i：5
    • a：5
    • ：9
  2. 按各个字符出现的次数进行编码，原则是出现次数越多的，则编码越小，比如空格出现了9次，编码为0
    • 0=
    • 1=a
    • 10=i
    • 11=e
    • 100=k
    • 101=l
    • 110=o
    • 111=v
    • 1000=j
    • 1001=u
    • 1010=y
    • 1011=d
  3. 按照上面的各个字符编码规定，最终的编码是

    10010110100……

根据颜色可以一一对应上面的编码规则，但是这种编码存在二义性。
比如前面三个字符100，这里是分成10，0，代表i，也可以划分成1，0，0，代表a。
解决这种二义性的办法，如下

前缀编码

字符的编码都不能是其他字符编码的前缀，符合此要求的编码叫做前缀编码，即不能匹配到重复的编码。
具体例子如下

赫夫曼编码

i like like like java do you like a java

  1. 统计每个字符对应的个数
    • d：1
    • y：1
    • u：1
    • j：2
    • v：2
    • o：2
    • l：4
    • e：4
    • i：5
    • a：5
    • ：9
  2. 按照上面字符出现的次数构建一颗赫夫曼树（看赫夫曼树的笔记），次数作为权值，字符也要记录在节点里面

image.png

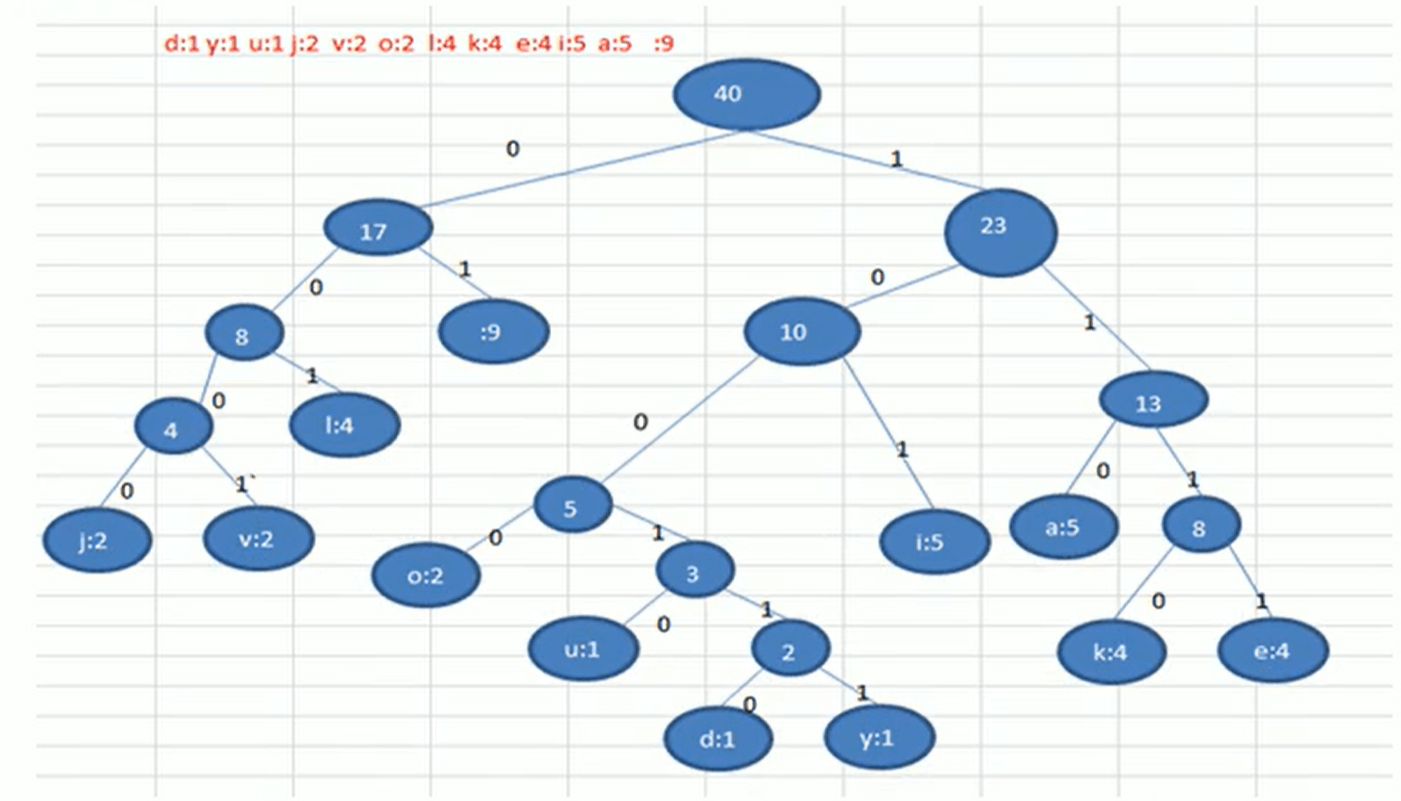
  1. 根据赫夫曼树给各个字符规定编码，向左的路径为0，向右的路径为1，编码如下：
    • o：1000
    • u：10010
    • d：100110
    • y：100111
    • i：101
    • a：110
    • k：1110
    • e：1111
    • j：0000
    • v：0001
    • l：001
    • ：01

赫夫曼编码是前缀编码，没有哪个编码是另一个编码的前缀，这样就不会出现多义性

  1. 按照赫夫曼编码，上面的字符对应的编码就是

    101010011011110111101001101111011110100110111101111010000110000111001100111100011001111000100100100110111101111011100100001100001110

如上编码，匹配数据时，从左到右，1没有，10没有，101，发现能匹配到i，101后面的0没有，01发现能匹配空格……

赫夫曼编码长度变成了132，压缩了(320-132)/320=58.75%

注意：
赫夫曼编码根据排序方法的不同，也可能不太一样，这样对应的赫夫曼编码不完全一样，但是WPL是一样的，都是最小的。所以最终的结果都是一样的

赫夫曼编码与解码代码

  1. using System;
  2. using System.Collections.Generic;
  3. using System.Globalization;
  4. using System.IO;
  5. using System.Runtime.Serialization.Formatters.Binary;
  6. using System.Text;
  8. namespace ConsoleApp1
  9. {
  10.     class Program
  11.     {
  12.         //生成赫夫曼树对应的赫夫曼编码，用字典存，key是原始数据，value是编码值
  13.         static Dictionary<byte, string> huffmanCodes = new Dictionary<byte, string>();
  14.         static void Main(string[] args)
  15.         {
  16.             string str = "i like like like java do you like a java";
  17.             //得到字节数组
  18.             byte[] bytes = Encoding.Default.GetBytes(str);
  20.             Console.WriteLine("赫夫曼编码后的字节数组");
  21.             byte[] hfcb = huffmanZip(bytes);
  22.             foreach (var b in hfcb)
  23.             {
  24.                 Console.Write(b + "  ");
  25.             }
  26.             Console.WriteLine();
  28.             Console.WriteLine("解码");
  29.             byte[] dbytes = decode(hfcb);
  30.             Console.WriteLine(Encoding.Default.GetString(dbytes));
  31.         }
  33.         #region 编码
  34.         //把数据字节数组做成节点集合
  35.         public static List<HFNode> getNodes(byte[] bytes)
  36.         {
  37.             List<HFNode> nodes = new List<HFNode>();
  38.             //存储每个byte出现的次数，用字典，唯一键
  39.             Dictionary<byte, int> weights = new Dictionary<byte, int>();
  40.             foreach(var b in bytes)
  41.             {
  42.                 bool bo =weights.ContainsKey(b);
  43.                 if (bo)
  44.                     weights[b] += 1;
  45.                 else
  46.                     weights.Add(b, 1);
  47.             }
  48.             //把每个键值对转换成nodes集合
  49.             foreach(var w in weights)
  50.             {
  51.                 nodes.Add(new HFNode(w.Value, w.Key));
  52.             }
  53.             return nodes;
  54.         }
  56.         //创建赫夫曼树
  57.         public static HFNode CreateHuffmanTree(List<HFNode> nodes)
  58.         {
  59.             while (nodes.Count > 1)
  60.             {
  61.                 //排序从小到大
  62.                 nodes.Sort();
  63.                 //取出前两棵最小的二叉树
  64.                 HFNode leftnode = nodes[0];
  65.                 HFNode rightnode = nodes[1];
  67.                 //合并成一颗新的二叉树
  68.                 HFNode parent = new HFNode(leftnode.weight + rightnode.weight, 0);
  69.                 parent.left = leftnode;
  70.                 parent.right = rightnode;
  72.                 //去掉已经使用的两个节点,加入新的节点
  73.                 nodes.Remove(leftnode);
  74.                 nodes.Remove(rightnode);
  75.                 nodes.Add(parent);
  76.             }
  77.             //nodes最后的一个节点就是赫夫曼树的根节点
  78.             return nodes[0];
  79.         }
  82.         //将传入的hfnode节点的所有叶子节点的赫夫曼编码得到
  83.         //node是传入节点
  84.         //code是路径：左子节点是0，又子节点是1
  85.         //path是用于拼接路径
  86.         public static void getCodes(HFNode node,string code,StringBuilder path)
  87.         {
  88.             path.Append(code);
  89.             if (node != null)
  90.             {
  91.                 //判断当前节点是叶子节点还是非叶子节点
  92.                 if (node.left!=null || node.right!=null)//左右子节点只要有一个不为null，就是非叶子节点
  93.                 {
  94.                     //递归
  95.                     getCodes(node.left, "0", path);
  96.                     getCodes(node.right, "1", path);
  97.                 }
  98.                 else//叶子节点
  99.                 {
  100.                     //表示找到了某个叶子节点的最后
  101.                     huffmanCodes.Add(node.data, path.ToString());
  102.                 }
  103.             }
  104.         }
  106.         //将字符串对应的byte[]数组，通过生成赫夫曼编码表，返回一个赫夫曼编码压缩后的byte[]
  107.         //bytes：原始数组
  108.         public static byte[] Zip(byte[] bytes)
  109.         {
  110.             //利用huffmanCodes将bytes转成赫夫曼编码对应的字符串
  111.             string hfcstr = "";//赫夫曼编码对应的字符串
  112.             StringBuilder strb = new StringBuilder();//用StringBuilder来拼接，速度快
  113.             foreach( var b in bytes)
  114.             {
  115.                 //在赫夫曼编码字典里面查找
  116.                 strb.Append(huffmanCodes[b]);
  117.             }
  118.             hfcstr = strb.ToString();
  119.             //Console.WriteLine(hfcstr);
  120.             //将hfcstr字符串，8位一字节的转换成一个byte[]数组
  121.             //先计算byte[]的长度，如果hfcstr%8有余数，始终都要+1，不如直接+7后/8,保留整数部分
  122.             int len = (hfcstr.Length + 7) / 8;
  123.             //创建存储压缩后的byte数组
  124.             byte[] hfcb = new byte[len];
  125.             int index = 0;//数组的计数器，记录第几个byte
  126.             for(int i = 0; i < hfcstr.Length; i += 8)//8位1字节所以步长+8
  127.             {
  128.                 //从i开始截取8个字符
  129.                 string strbyte = "";
  130.                 if (i + 8 > hfcstr.Length)//最后一次，不够8位
  131.                     strbyte += hfcstr.Substring(i);
  132.                 else
  133.                     strbyte += hfcstr.Substring(i, 8);
  134.                 //将strbyte转换成byte放入到hfcb里面
  135.                 hfcb[index++] = Convert.ToByte(strbyte,2);
  136.             }
  137.             return hfcb;
  138.         }
  140.         /// <summary>
  141.         /// 赫夫曼压缩总方法
  142.         /// </summary>
  143.         /// <param name="bytes">原始字节数组</param>
  144.         /// <returns></returns>
  145.         public static byte[] huffmanZip(byte[] bytes)
  146.         {
  147.             //1.根据原始字节数据，得到赫夫曼节点集合
  148.             List<HFNode> hfl = getNodes(bytes);
  149.             //2.根据赫夫曼节点集合创建赫夫曼树，得到根节点
  150.             HFNode root = CreateHuffmanTree(hfl);
  151.             //3.得到赫夫曼编码字典
  152.             getCodes(root, "", new StringBuilder());
  153.             //4.得到一个赫夫曼编码压缩后的字节数组
  154.             byte[] hfcb = Zip(bytes);
  156.             return hfcb;
  157.         }
  159.         #endregion
  161.         #region 解码
  162.         //将一个byte转换成一个二进制的字符串,flag:最后一个字节不用补高位，这儿flag就是判断是否补高位的
  163.         public static string byteTobitstring(byte b,bool flag)
  164.         {
  165.             string bitstr = Convert.ToString(b,2);//转换成二进制字符串
  166.             if (flag)//要补高位
  167.             {
  168.                 int len = 8 - bitstr.Length;
  169.                 for (int t = 0; t < len; t++)
  170.                     bitstr = "0" + bitstr;
  171.             }
  172.             return bitstr;
  173.         }
  175.         /// <summary>
  176.         /// 赫夫曼解码.
  177.         /// </summary>
  178.         /// <param name="huffmanBytes">传入一个赫夫曼编码后的一个字节数组</param>
  179.         /// <returns></returns>
  180.         public static byte[] decode(byte[] huffmanBytes)
  181.         {
  182.             //先得到huffmanBytes对应的二进制字符串
  183.             string bitstr = "";
  184.             StringBuilder sb = new StringBuilder();//用StringBuilder拼接速度快
  185.             for(int i = 0; i < huffmanBytes.Length; i++)
  186.             {
  187.                 //判断是否是最后一个字节，如果是最后一个字节，不用补高位，是多少位就是多少位数
  188.                 bool b = !(i == huffmanBytes.Length - 1);
  189.                 sb.Append(byteTobitstring(huffmanBytes[i], b));
  190.             }
  191.             bitstr = sb.ToString();
  192.             Console.WriteLine("得到对应的二进制字符串完成");
  193.             //Console.WriteLine(bitstr);
  194.             //把字符串按照指定的赫夫曼编码进行解码
  195.             //原来的字典是通过字符ASCII码查询赫夫曼编码，现在重新建一个字典，反过来通过赫夫曼编码查询字符ASCII码
  196.             Dictionary<string, byte> hfcodes = new Dictionary<string, byte>();
  197.             foreach(var a in huffmanCodes)
  198.                 hfcodes.Add(a.Value, a.Key);
  199.             //创建一个集合存放byte
  200.             List<byte> list = new List<byte>();
  201.             //扫描bitstr,i就是每个字符的指针
  202.             for(int i = 0; i < bitstr.Length; i++)
  203.             {
  204.                 //长度，从i开始多少长度的字符串，是一个赫夫曼编码。这个长度区间在1——bitstr.Length - i之间，一定得是<=,能匹配到最后一个字符
  205.                 for (int t = 1; t <= bitstr.Length - i; t++)
  206.                 {
  207.                     //判断从i开始，取t个字符的字符串是不是已经存在的赫夫曼编码，
  208.                     bool b = hfcodes.ContainsKey(bitstr.Substring(i, t));
  209.                     if(b)
  210.                     {
  211.                         //如果是赫夫曼编码，就把数据字符的ASCII码加入到list中
  212.                         list.Add(hfcodes[bitstr.Substring(i, t)]);
  213.                         i += t-1;//从0开始到i+t之前的字符串已经扫描过了，现在从i+t开始，为什么要t-1，因为这里退出后，进入外层循环，i++，先-1，在++，就保持不变
  214.                         break;
  215.                     }  
  216.                 }
  217.             }
  218.             //到这里list里面就已经存放了所有字符的ASCII码
  219.             return list.ToArray();
  220.         }
  222.         #endregion
  224.         /// <summary>
  225.         /// 赫夫曼节点实现IComparable接口，作用是进行排序
  226.         /// </summary>
  227.         public class HFNode : IComparable<HFNode>
  228.         {
  229.             public int weight;//权值，表示字符出现的次数
  230.             public byte data;//存放数据本身，比如'a'==97,' '==32,存放ASCII码
  231.             public HFNode left;
  232.             public HFNode right;
  233.             public HFNode(int weight,byte data)
  234.             {
  235.                 this.weight = weight;
  236.                 this.data = data;
  237.             }
  238.             //实现接口方法
  239.             public int CompareTo(HFNode hfnode)
  240.             {
  241.                 //从小到大排序
  242.                 return this.weight - hfnode.weight;
  243.             }
  245.             //前序遍历
  246.             public void preOrder()
  247.             {
  248.                 Console.WriteLine(this.weight);
  249.                 if (this.left != null)
  250.                     this.left.preOrder();
  251.                 if (this.right != null)
  252.                     this.right.preOrder();
  253.             }
  254.         }
  255.     }
  256. }

赫夫曼编码压缩文件代码

  1. using System;
  2. using System.Collections.Generic;
  3. using System.Globalization;
  4. using System.IO;
  5. using System.Runtime.Serialization.Formatters.Binary;
  6. using System.Text;
  8. namespace ConsoleApp1
  9. {
  10.     class Program
  11.     {
  12.         //生成赫夫曼树对应的赫夫曼编码，用字典存，key是原始数据，value是编码值
  13.         static Dictionary<byte, string> huffmanCodes = new Dictionary<byte, string>();
  14.         static void Main(string[] args)
  15.         {
  16.             //zipFile(@"D:\B\a.pdf", @"D:\B\a.dat");
  17.             unzipFile(@"D:\B\a.dat", @"D:\B\Aa.pdf");
  18.         }
  20.         //省略部分和上面一样
  21.         #region 编码
  22.         public static List<HFNode> getNodes(byte[] bytes){}
  23.         public static HFNode CreateHuffmanTree(List<HFNode> nodes){}
  24.         public static void getCodes(HFNode node,string code,StringBuilder path){}
  25.         public static byte[] Zip(byte[] bytes){}
  26.         public static byte[] huffmanZip(byte[] bytes){}
  27.         #endregion
  29.         #region 解码
  30.         public static string byteTobitstring(byte b,bool flag){}
  31.         public static byte[] decode(byte[] huffmanBytes){}
  32.         #endregion
  34.         #region 文件压缩
  35.         public static void zipFile(string srcFileName,string dstFileName)
  36.         {
  37.             FileStream srcstream = new FileStream(srcFileName, FileMode.Open, FileAccess.Read);
  38.             byte[] b = new byte[srcstream.Length];
  39.             srcstream.Read(b, 0, b.Length);
  41.             byte[] hfcb = huffmanZip(b);
  43.             //序列化两个东西到文件里面，赫夫曼字节数组，和赫夫曼编码字典
  44.             FileStream dststream = new FileStream(dstFileName, FileMode.OpenOrCreate, FileAccess.Write);
  45.             BinaryFormatter formatter = new BinaryFormatter();
  46.             formatter.Serialize(dststream, hfcb);
  47.             formatter.Serialize(dststream, huffmanCodes);
  49.             srcstream.Dispose();
  50.             dststream.Dispose();
  51.             Console.WriteLine("压缩成功");
  52.         }
  54.         public static void unzipFile(string zipFileName,string dstFileName)
  55.         {
  56.             FileStream zipstream = new FileStream(zipFileName, FileMode.Open, FileAccess.Read);
  58.             BinaryFormatter formatter = new BinaryFormatter();
  59.             byte[] hfbs = (byte[])formatter.Deserialize(zipstream);
  60.             huffmanCodes = (Dictionary<byte, string>)formatter.Deserialize(zipstream);
  62.             Console.WriteLine("反序列化完成");
  63.             //解压赫夫曼编码
  64.             byte[] bytes = decode(hfbs);
  66.             Console.WriteLine("解压赫夫曼编码完成");
  67.             //输出文件
  68.             FileStream dststream = new FileStream(dstFileName, FileMode.OpenOrCreate, FileAccess.Write);
  69.             dststream.Write(bytes, 0, bytes.Length);
  71.             zipstream.Dispose();
  72.             dststream.Dispose();
  73.             Console.WriteLine("解压成功");
  74.         }
  75.         #endregion
  76.         public class HFNode : IComparable<HFNode>{}
  77.     }
  78. }