克鲁斯卡尔算法介绍

  • 克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法
  • 基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路

  • 具体做法：首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止

    问题描述

    image.png

  • 某城市新增7个站点(A, B, C, D, E, F, G) ，现在需要修路把7个站点连通

  • 各个站点的距离用边线表示(权) ，比如 A – B 距离 12公里
  • 问：如何修路保证各个站点都能连通，并且总的修建公路总里程最短?

图解

  1. 把边的权值排好序，选择权值最小的一条边，[2]

image.png

  1. 继续选择剩余的边，权值最小的，[3]

image.png

  1. 继续选择剩余权值最小的边，[4]

image.png

  1. 下一个权值最小的是[5]，但是C的终点是F，E的终点也是F，也就是说CE的终点相同，构成回路，所以不能选择CE
  2. 继续下一个，[6]，同样，CF的终点都是F，构成回路
  3. 下一个[7]，BF的终点不相同，不构成回路，所以选择BF

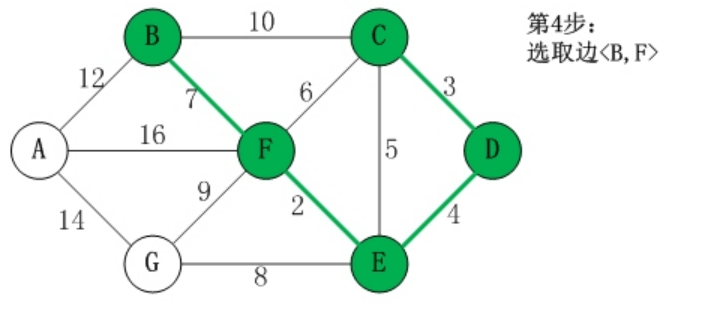
image.png

  1. 如上的选择方式同理，选择剩下的部分

image.png
image.png

代码

  1. using System;
  2. using System.Collections.Generic;
  3. using System.Globalization;
  4. using System.IO;
  5. using System.Runtime.Serialization.Formatters.Binary;
  6. using System.Text;
  8. namespace ConsoleApp1
  9. {
  10.     class Program
  11.     {
  13.         static void Main(string[] args)
  14.         {
  15.             char[] vertexs = new char[] { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
  16.             //邻接矩阵的关系使用二维数组
  17.             //比如C和G之间不连通，就用8888来表示，权值太大就不考虑了
  18.             int x = 8888;
  19.             int[,] matrix = new int[,]
  20.             {
  21.                 //A   B   C   D   E   F   G
  22.                 /*A*/{0 , 12, x , x , x , 16, 14 },
  23.                 /*B*/{12, 0 , 10, x , x , 7 , x  },
  24.                 /*C*/{x , 10, 0 , 3 , 5 , 6 , x  },
  25.                 /*D*/{x , x , 3 , 0 , 4 , x , x  },
  26.                 /*E*/{x , x , 5 , 4 , 0 , 2 , 8  },
  27.                 /*F*/{16, 7 , 6 , x , 2 , 0 , 9  },
  28.                 /*G*/{14, x , x , x , 8 , 9 , 0  }
  29.             };
  31.             KruskalCase kruskal=new KruskalCase(vertexs, matrix);
  32.             kruskal.print();
  33.             Console.WriteLine("没排序");
  34.             EData[] edatas = kruskal.getEdges();
  35.             foreach(var edata in edatas)
  36.             {
  37.                 edata.print();
  38.             }
  39.             Console.WriteLine("排序完");
  40.             kruskal.sortEdges(edatas);
  41.             foreach (var edata in edatas)
  42.             {
  43.                 edata.print();
  44.             }
  45.             kruskal.kruskal();
  46.         }
  48.     }
  51.     class KruskalCase
  52.     {
  53.         private int edgeNum;//边的个数
  54.         private char[] vertexs;//顶点数组
  55.         private int[,] matrix;//邻接矩阵
  56.         public KruskalCase(char[] vertexs,int[,] matrix)
  57.         {
  58.             this.vertexs = vertexs;
  59.             this.matrix = matrix;
  60.             //统计边的数量,j=i+1,自己跟自己就没有必要再进行连接了
  61.             for(int i = 0; i < matrix.GetLength(0); i++)
  62.             {
  63.                 for(int j = i+1; j < matrix.GetLength(1); j++)
  64.                 {
  65.                     if (this.matrix[i, j] != 8888)
  66.                     {
  67.                         edgeNum++;
  68.                     }
  69.                 }
  70.             }
  71.         }
  73.         //克鲁斯卡尔算法
  74.         public void kruskal()
  75.         {
  76.             int index = 0;//最后结果数组的索引
  77.             int[] ends = new int[vertexs.Length];//用于保存 "已有最小生成" 中的每个顶点在最小生成树中的终点
  78.             //创建结果数组，保存最后的最小生成树
  79.             EData[] rets=new EData[vertexs.Length-1];
  80.             //获取图中所有边的集合
  81.             EData[] edges = getEdges();
  82.             //按照边的权值大小排序
  83.             sortEdges(edges);
  84.             //遍历edges数组，将边添加到最小生成树中时，判断准备加入的边是否构成了回路，如果没有就加入rets,否则就不能加入
  85.             for(int i = 0; i < edgeNum; i++)
  86.             {
  87.                 //获取到第i条边的第一个顶点(起点),第二个顶点(终点)
  88.                 int p1 = getPosition(edges[i].start);
  89.                 int p2 = getPosition(edges[i].end);
  91.                 //获取p1,p2这个顶点在已有的最小生成树中的终点
  92.                 int m = getEnd(ends, p1);
  93.                 int n = getEnd(ends, p2);
  94.                 //判断是否构成回路
  95.                 if (m != n)//两条边的终点不一样就没有构成回路
  96.                 {
  97.                     ends[m] = n;//设置m在已有最小生成树的终点
  98.                     rets[index++] = edges[i];//有一条边入选了
  99.                 }
  100.             }
  101.             Console.WriteLine("最小生成树");
  102.             foreach (var ret in rets)
  103.             {
  104.                 ret.print();
  105.             }
  106.         }
  108.         //打印邻接矩阵
  109.         public void print()
  110.         {
  111.             for (int i = 0; i < matrix.GetLength(0); i++)
  112.             {
  113.                 for (int j = 0; j < matrix.GetLength(1); j++)
  114.                     Console.Write(matrix[i, j] + "  ");
  115.                 Console.WriteLine();
  116.             }
  117.         }
  118.         //对边进行排序处理，这里用冒泡
  119.         public void sortEdges(EData[] edges)
  120.         {
  121.             for(int i = 0; i < edges.Length; i++)
  122.             {
  123.                 for (int j = 0; j < edges.Length - 1 - i; j++)
  124.                 {
  125.                     if (edges[j].weight > edges[j + 1].weight)//交换
  126.                     {
  127.                         EData temp = edges[j];
  128.                         edges[j] = edges[j + 1];
  129.                         edges[j+1] = temp; ;
  130.                     }
  131.                 }
  132.             }
  133.         }
  135.         //返回ch顶点对应的下标，找不到返回-1
  136.         public int getPosition(char ch)
  137.         {
  138.             for(int i =0;i<vertexs.Length;i++)
  139.                 if (vertexs[i] == ch)
  140.                     return i;
  141.             return -1;
  142.         }
  144.         //获取图中的边，放到EData[]数组中，后面需要遍历该数组
  145.         //通过matrix邻接矩阵来获取
  146.         public EData[] getEdges()
  147.         {
  148.             int index = 0;
  149.             EData[] edges = new EData[edgeNum];
  150.             for(int i = 0; i < vertexs.Length; i++)
  151.             {
  152.                 for(int j = i + 1; j < vertexs.Length; j++)
  153.                 {
  154.                     if (matrix[i, j] != 8888)
  155.                     {
  156.                         edges[index++] = new EData(vertexs[i], vertexs[j], matrix[i, j]);
  157.                     }
  158.                 }
  159.             }
  160.             return edges;
  161.         }
  163.         //获取下标为i的顶点的终点，用于后面判断两个顶点的终点是否相同
  164.         //ends记录了各个顶点对应的终点是哪个，ends是在遍历过程中逐步行程的
  165.         //i表示传入的顶点对应的下标
  166.         //返回i这个顶点对应的终点的下标
  167.         public int getEnd(int[] ends,int i)
  168.         {
  169.             while (ends[i] != 0)
  170.                 i = ends[i];
  171.             return i;
  172.             /*
  173.              * 一开始ends这个数组是这样的[0,0,0,0,0,0,0]
  174.              * i表示传入的顶点的下标，如果这个下标为0，说明这个顶点还没有终点，为0都不进while，直接返回这个下标
  175.              * 比如EF这条边，
  176.              * m = E这个点下标为4，最开始传入的时候ends[4]==0,所以直接返回4出去
  177.              * n = F这个点下标为5，直接返回5
  178.              * m和n不相同，所以不构成回路，这条边可以加入，加入后，就要设置ends，ends[4]=5
  179.              * [0,0,0,0,5,0,0]
  180.              * 表示什么意思,第4个顶点，就是E的终点是5，5指向F，所以E的终点是F。
  181.              * 下次检测的时候，如果传入的是4，返现ends[4]!=0,说明设置了终点，就把终点的下标赋值给当前下标，循环检测
  182.              */
  183.         }
  185.     }
  187.     //边
  188.     class EData
  189.     {
  190.         public char start;//边的一个点
  191.         public char end;//边的另一个点
  192.         public int weight;//边的权值
  193.         public EData(char start,char end,int weight)
  194.         {
  195.             this.start = start;
  196.             this.end = end;
  197.             this.weight = weight;
  198.         }
  199.         public void print()
  200.         {
  201.             Console.WriteLine($"起始{start}，结束{end}，权值{weight}");
  202.         }
  203.     }
  204. }