一、简单的解方程

1. 例子

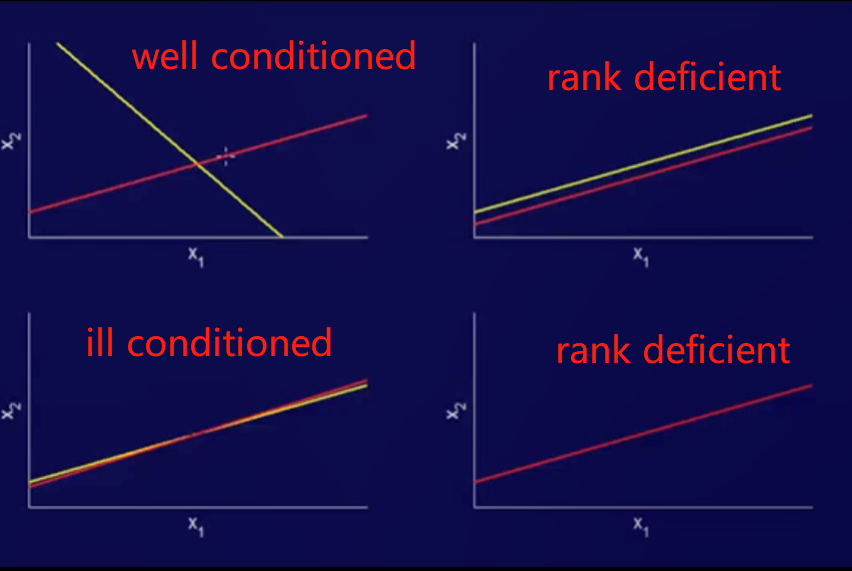
2. Stability and condition

• Stability是算法（方法）的性质，condition是问题（problem）本身的性质。

二、Cramer’s rule

• 法则

• 例子 ```python import numpy as np

系数矩阵

A = np.matrix(np.random.randint(1,10, size=(4,4)))

解

x = np.matrix([1,2,3,4]).reshape((4,1)) print(A*x)

得到b

b = np.matrix([[59],[56],[56],[49]])

Cramer’s rule

A1 = A.copy() A1[:,0]=b

A2 = A.copy() A2[:,1]=b

A3 = A.copy() A3[:,2]=b

A4 = A.copy() A4[:,3]=b

x1 = np.linalg.det(A1) / np.linalg.det(A) x2 =np.linalg.det(A2) / np.linalg.det(A) x3 =np.linalg.det(A3) / np.linalg.det(A) x4 =np.linalg.det(A4) / np.linalg.det(A) ```

三、Elimination

• 目标：从方程组中消除某些x变量。
• 例子

因此，Cramer=Elimination

四、Naive Gauss Elimination

1. 图解算法

• 例子，

• Forward elimination
  • 第一轮迭代
    • 首先对第[1]行乘以，得到；然后，第[2]行减去[4]，得到新的第二行
    • 同理，对第[3]行进行同样的操作，将第[3]行-(第[1]行*)，得到新的第三行
    • 因此，第一轮结果为

• 第二轮迭代
  • 接着，将新的第3行 - 新的第2行*，得到

从而有。

• Back substitution
  • 先解出，再得到。

2. 算法说明

• 前向迭代
  • 最外层一共迭代n-1次，记号为k；
  • 第1次迭代，从第2行开始，将第2行-第1行，第3行-第1行，第n行-第1行*，得到第1次更新的结果；
  • 第2次迭代从第3行开始，将第3行-新的第2行，将第4行-新的第2行，将第n行-新的第2行*，得到第2次更新的结果；
  • 在第k次迭代从第k+1行开始；此刻第k行的结果是，第(k+1)行的结果是；
    • 将第k+1行-第k行*，得到了第k次迭代的第k+1行结果，以此类推，k+2~n行都要和第k行进行相同操作；那么k+1~n行得到了第k次的更新的结果；
  • 里面的循环是，在第i行，从第i个元素开始更新该行元素。
• 在得到了上三角矩阵U之后，通过后向迭代，求解每个x；
  • 首先，得到最后一个；
  • 然后求解倒数第二个；
  • 以此类推。

3. C++代码

五、Gauss-Jordan Elimination

• 消元+正态化

依次往下，每次消元+标准化为1。

六、Gauss Elimination缺点

• 如果是0，那么整个方法就失效了；使用permutation matrix，PAx=Pb解决；
• roundoff error；
• ill-conditioned systems。

七、LU Decomposition

1. 简要步骤

• 第一步，将矩阵分解为；
• 第二步forward substitution，分解出，从而；
• 第三步back substitution，解x，。

2. 详解

• 将A分解为LU；
  • 通过Gauss Elimination，我们得到了上三角矩阵，

，,
过程是第2行-第一行乘以，第3行-第一行乘以，第三行-第二行乘以。

• 在此过程中，得到了L矩阵，

• 分解出（Forward substitution）
  • 得到了L之后，

• 解出x（Back substitution）
  • 

3. 使用LU分解找到逆矩阵

• 当系数矩阵A重复使用的时候，那么使用LU分解将会简化。
• 
  

4. 使用LU分解找到A的行列式

5. 使用LU分解找到A的条件

\scriptsize
\begin{aligned}
\left(
\begin{array}{c}
\end{array}
\right)
\end{aligned}