主要内容:
- 误差来源
- 有效数字
- 有没有小数点
- 误差
- 舍入误差
零、误差的来源
一、有效数字
- 定义1:没有小数点的数:从左边的第一个非零数字到右边最后的非零数字之间的所有数字,例如12000有两个有效数字“1”“2”。
- 定义2:有小数点的数:从左边第一个非零数字到右边最后的数字(不管是否为0),例如2000.5有5个有效数字,2000.5000有8个有效数字,0.0001有一个有效数字,0.000100有三个有效数字。
- 有效数字:只有最后一位是不准确的。例如,如果某个重量为10.5g,那么有效数字为3个,那么大概介于10.45~10.55之间;如果重量是10.500g,那么有效数字是5个,那么重量介于10.495~10.505之间。
二、迭代(Iterative refinement)VS 直接(Direct)
- 迭代:从一个处置开始,然后越来越接近真值;
- 直接:一步到位真值。
三、误差定义
- 误差:真值和近似值之间的差
- 绝对误差
真值true value - 近似值approx,相对误差
误差/真值。相对误差更有效地测量准确程度,因为和单位无关。
- 百分比真实相对误差(true percent relative error)
——we don’t know.
- Percent approximation error =
——we know it.
- 在迭代计算过程中,每一步的误差
,一般而言,只要定义一个百分比公差eps,当误差下降到eps内,那么停止计算。
- 绝对误差
- Newton-Raphson求方程的解
四、舍入误差Roundoff error
1. Quantization error
- 数字在计算机中如何表示:
- 整数(Integer)
- 固定点(Fixed-point)
- 浮点(Floating-point)
- 整数表达:16位二正数进制的表达的范围-32768~32767。

左边第一位是符号位置,1=负数,0=正数;
剩下的15个位置表示数字,右边第一个位置是,右边第二个位置是
,左边第二个位置是
;对应位置的01表示01和对应的2的指数幂相乘。
- 0的表达:
;
- 最大正数:
;
- 第二个最大负数:
;
- 最大的负数:
,这是因为0的表达已经是16个0,因此这里特指1+15个0是最大的负数(虽然计算方式和上面的相悖)。
- 因此,范围是-32768~32767。
- 浮点数的表示;那么整数部分称为exponent(characteristic),分数部分称为mantissa(significand)。
,m=mantissa,b=base,e=exponent,中间的点是乘号;例如10进制base=10,二进制中base=2;
- Normalization:丢掉多余的0,例如0.05=
;
- 标准,
;
- 例如,10进制中,存在
;二进制中,存在
。
- 标准,

- 例子,使用7位二进制的浮点数表达,左边第一位是整体的正负符号,第二位是幂的正负符号,三四两位是幂的大小,5~7位是整数位置的大小。找到最小的正数。

那么第一位=0,表示正数;第二位幂的符号取负数;三四两位得到最大的幂=12^1+12^0=3;5~7位是整数m的位置(需要处在0.5<=m<1之间),最小=0.5+0+0=0.5,因此最小的正数=0.5*2^{-3}=0.0625
第二小的正数=2^{-3}(12^{-1}+02^{-2}+12^{-3})
最大的正数=2^{3}(2^-1+2^-2+2^-3)=7。
在这个数值系统中,不仅仅存在overflow的问题(不能超出-7~7的范围),也存在underflow的问题,不能够小于0.0625的误差;随着数字增大,*数字之间的空隙(无法表达的数字)也越来越大。
const float a = 1.234; const float b = 0.0000005678; const double c = 1.234; const double d = 0.0000005678;
class p1
{
private:
float x;
double y;
public:
void floating()
{
x = a + b;
y = c + d;
cout.setf(ios::fixed, ios::floatfield); //固定格式
cout.precision(10); //高精度
cout << x << endl;
cout << y << endl;
}
};
int main()
{
p1 p;
p.floating();
return 0;
}
```
结果:x=1.2340005636,y=1.2340005678。
如果设定精度为15位,那么结果为x=1.234000563621521,y=1.234000567800000。
因此,double更加准确。
2. Numerical manipulations
- 各种运算
- Stability and condition
- Stability:算法的问题。
- Condition:问题本身的条件不好。
五、Truncation error
- 例子
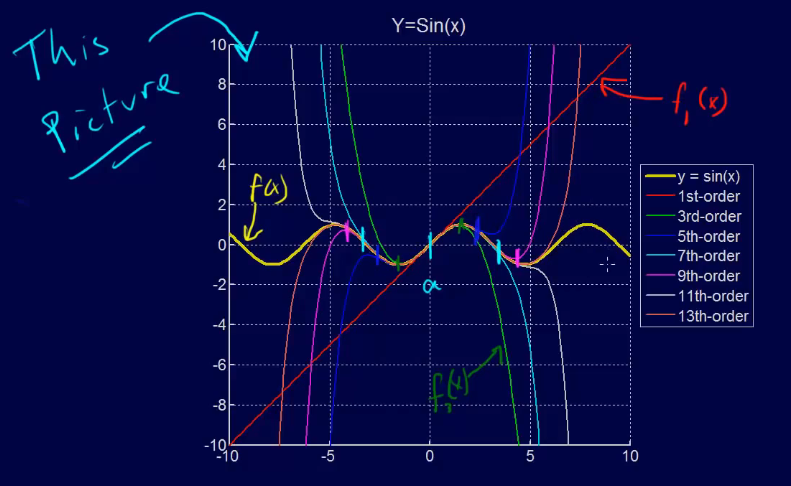
这里a表示开始拟合的位置。
2. 误差的表示
- 推导
- 积分均值的第一定理
- 积分均值的第二定理
积分均值的第一定理即为第二定理的特殊情况,h(t)=1。
- 那么令

