二叉树由一个根节点加上两个互不相交的左右子树构成,或者是一个没有结点的空树。
- 每个结点最多有两个子结点。
- 左子树和右子树不可互换,是有序的。
例如,结点A 为根节点,以结点B 为根节点的子树为左子树,以结点C为根节点的子树称为右子树。
二叉树的5种基本形态
- 空树
- 只含根节点
- 右子树为空
- 左子树为空
- 左右子树都不为空
满二叉树和完全二叉树
- 满二叉树 —>> 每一层都充满结点
- 叶子结点只能在最后一层
- 非叶子结点的度一定是2
- 在同样深度的二叉树中
- 满二叉树的结点数最多(因为每个结点都有两个孩子);
- 拥有的叶子结点的个数也最多(因为每个结点都有两个孩子,一直到最后一层叶子结点,必然是最多的);
- 在相同结点数的树中,满二叉树的深度最小。
- 完全二叉树 —>> 最后一层结点可以不满,但必须集中在左边。
- 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
- 某结点的度如果为1,则它只有左孩子。
- 叶子结点只能出现在最后两层。
- 相同结点的树中,完全二叉树的深度最小。
二叉树的性质
- 性质1
第 a 层的节点数,至多为 2a-1 - 性质2
深度为 k 的二叉树,节点数至多为 2k - 1 个 - 性质3
若 nk 代表度(孩子个数)为 k 的结点个数,则 n0 = n2 + 1(叶子节点数 = 2度结点树 + 1) - 性质4
具有 n 个结点的完全二叉树,深度 k = log2n + 1 - 性质5
将具有 n个结点的完全二叉树按照一维数组方式从左到右,从上层到子层,从0开始编号,编号为j的结点- 根节点编号为0
- 左子树根节点为 2j + 1,右子树为 2(j + 1)
- 判断有子树(即是判断是否有左子树)
2j + 1 ≤ n - 1,推导出 2j + 1 < n - 判断左右子树都有(即是判断有右子树)
2(j + 1) ≤ n - 1
二叉树的存储方式
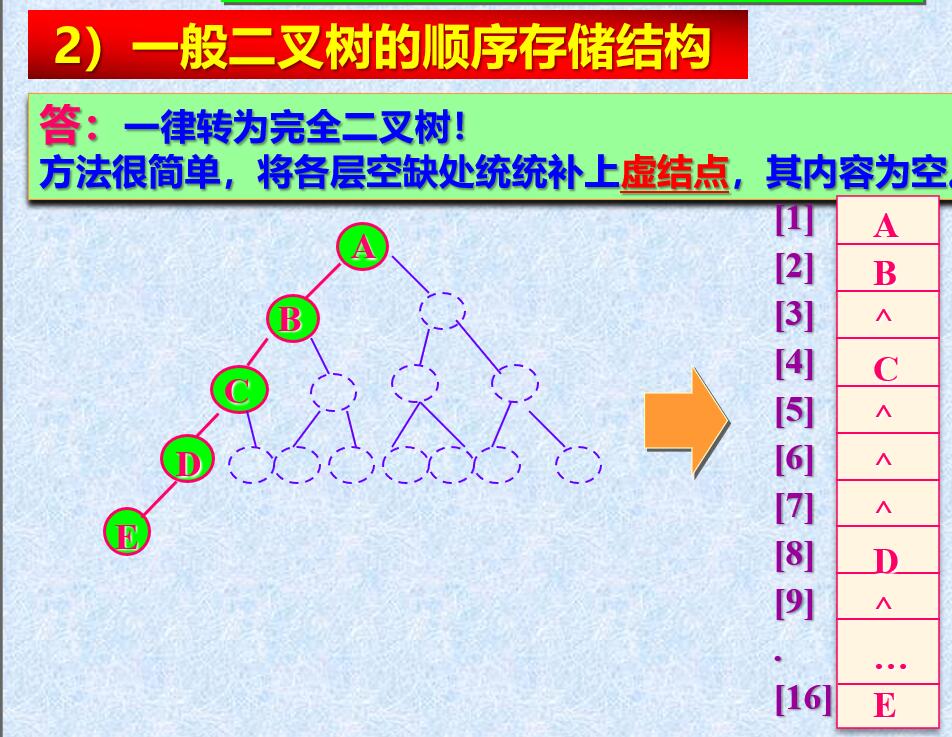
- 顺序存储
将二叉树转换为完全二叉树进行存储。- 顺序存储的方式缺陷
- 转换为完全二叉树,浪费空间
- 新一层数据的插入不方便。
- 删除非叶子节点不方便。
- 顺序存储的方式缺陷
- 链式存储方式
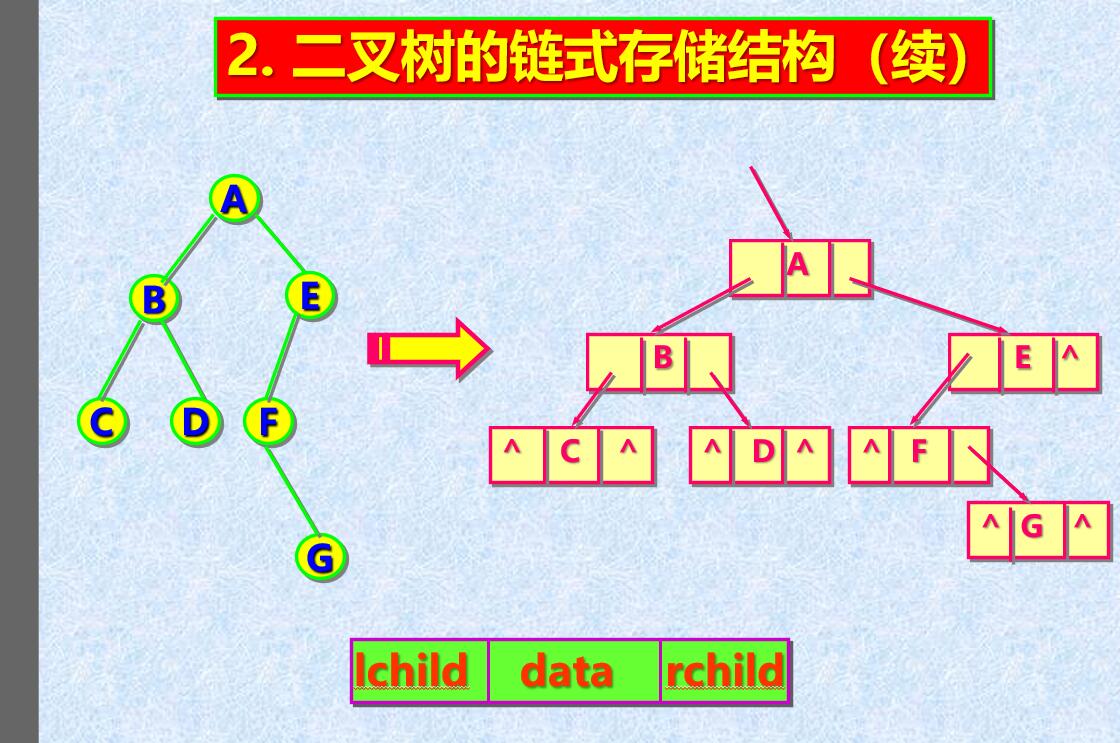
二叉树的链式表示
- 由于顺序存储方式劣势比较明显,平常用到的表示方式都是链式表示。
二叉树的存储结构
- 采用链式存储的方式,结点只存单个元素值,节点之间通过指针联系,维持集合的关系。
- 这里定义了左右孩子指针的bool标记变量,标记是否用来存放前驱和后继。
```c
// 定义返回状态及返回码
define Status int
define OK 1
define ERROR 0
// 定义存储的元素类型define ElementType int
// 二叉树结点结构定义 typedef struct BinaryTreeNode { // 数据域 BiTreeNodeElementType data; // 指向左孩子的指针 BinaryTreeNode left; // 左指针功能标记,为true则指向前驱 bool ltag = false; // 指向右孩子的指针 BinaryTreeNode right; // 右指针功能标记,为true则指向后继 bool rtag = false; }BTNode, *BinaryTree;
> 二叉树的常用操作- 初始化- 拿到一个指向根结点的指针,即可确定一个二叉树```c/* 01_二叉树——初始化*/Status initBiTree_T(BinaryTree& biTree){biTree = NULL;return OK;}
销毁
- 销毁一个二叉树结点是通过指向该结点的指针进行的。
- 如果结点为空,则不需要进行操作
- 如果结点不为空,则需要先删除左右孩子结点,再删除该结点
/* 02_二叉树——销毁*/Status destroyBiTree_T(BinaryTree& biTree){// 如果结点不为空if (biTree){biTree->parent = NULL;// 先删除左右子树if (destroyBiTree_T(biTree->left) && destroyBiTree_T(biTree->right)){return OK;}// 再删除该结点delete biTree;}return OK;}
- 销毁一个二叉树结点是通过指向该结点的指针进行的。
判空(是否为空树)
- 即是判断根节点是否为空
/* 03_二叉树——判空*/Status emptyBiTree_T(BinaryTree biTree){return biTree == NULL ? OK : ERROR;}
- 即是判断根节点是否为空
求深度
- 利用树的递归,采用累加的方式求得。
- 如果一个结点不为空,则该层的深度为1
- 一个结点的深度,即是其左结点深度,与右节点的深度的较大者,加上本层的深度1。 ```c / 04_二叉树——深度/ int treeDepth_T(BinaryTree biTree) { // 该结点为空,则该层深度为0 if (!biTree) { return 0; } // 否则,该层深度有1,要向上累加 else { int leftDepth = treeDepth_T(biTree->left); int rightDepth = treeDepth_T(biTree->right); // 左右子树的深度,加上本层的深度1,即是该结点的深度 return 1 + max(leftDepth, rightDepth); } }
/返回两个数较大的一个/ int max(int a, int b) { return a > b ? a : b; }
- 是否叶子结点- 左右孩子都不存在,即是叶子结点```c/* 05_二叉树——是否是叶子结点*/Status leafBiNode_T(BinaryTree biTree){// 左右孩子都不存在,即为叶子结点return (biTree->left == NULL && biTree->right == NULL) ? OK : ERROR;}
求父节点
- 如果当前结点为空或,返回空。
- 通过遍历左右子树找其父结点,若找到,则将父结点指针回溯。
/* 06_二叉树——求父结点*/BinaryTree parentBiNode_T(BinaryTree biTree, BinaryTree target){if (!biTree){return NULL;}if (biTree->left == target || biTree->right == target){return biTree;}// 若左子树未找到,则找右子树BinaryTree parent = parentBiNode_T(biTree->left, target);if (!parent){parent = parentBiNode_T(biTree->right, target);}// 将结果回溯上去return parent;}
深度优先遍历方式
- 递归的前中后序遍历
- 递归方式非常简单,注意好控制终止条件,按定义的遍历顺序即可。 ```c / 08二叉树——先序遍历递归/ void preOrderTraverse_Recur(BinaryTree biTree) { if (!biTree) { return; } visit(biTree); preOrderTraverse_Recur(biTree->left); preOrderTraverse_Recur(biTree->right); }
- 递归的前中后序遍历
/ 09二叉树——中序遍历递归/ void inOrderTraverse_Recur(BinaryTree biTree) { if (!biTree) { return; } inOrderTraverse_Recur(biTree->left); visit(biTree); inOrderTraverse_Recur(biTree->right); }
/ 10二叉树——后序遍历递归/ void postOrderTraverse_Recur(BinaryTree biTree) { if (!biTree) { return; } postOrderTraverse_Recur(biTree->left); postOrderTraverse_Recur(biTree->right); visit(biTree); }
- 先序遍历_非递归(根 –> 左 --> 右)```c/* 12_二叉树——先序遍历_非递归*/void preOrderTraverse_NonRecur(BinaryTree biTree){if (!biTree){return;}// 采用栈存放当前结点的引用,用于左子树遍历完成,找到其右子树SqStack nodeStack;initStack_Sq(nodeStack);BinaryTree popped = NULL;// 外层:每一次循环完成一次左分支while (!stackEmpty_Sq(nodeStack) || biTree){// 对左分支的迭代,是一个访问和压栈的过程while (biTree){// 先序遍历的关键,优先访问根结点visit(biTree);push_Sq(nodeStack, biTree);// 对左结点的迭代biTree = biTree->left;}// 一次左分支完成if (!stackEmpty_Sq(nodeStack)){// 左分支结束,则将其父结点出栈popped = (BinaryTree)malloc(sizeof(BinaryTreeNode));pop_Sq(nodeStack, popped);// 迭代到待访问的右孩子,下次循环执行访问biTree = popped->right;}}destroyStack_Sq(nodeStack);}
- 按照先序遍历规则,遇到任意一个非空结点,即优先访问,所以过程为:- 访问它;- 将它压栈;- 迭代其左孩子;- 访问完成左孩子,- 将栈顶元素(以上的非空结点)出栈;- 通过该出栈元素继续迭代其右孩子。- 过程控制- 将非空的控制放到while循环条件中,所以循环体内不用考虑当前结点的左右孩子非空性质。- 入栈的结点是根结点。- 内层循环,一次循环表示一次赋值到其左孩子的过程。- 外层循环是控制遍历过程。一次循环代表一个结点的左子树的完成过程。以栈的非空性和当前结点的非空性共同决定是否还需继续遍历。
中序遍历_非递归(左 —> 中 —> 右)
/* 13_二叉树——中序遍历_非递归*/void inOrderTraverse_NonRecur(BinaryTree biTree){if (!biTree){return;}SqStack nodeStack;initStack_Sq(nodeStack);BinaryTree popped = NULL;while (!stackEmpty_Sq(nodeStack) || biTree){// 遇到左孩子即压栈while (biTree){push_Sq(nodeStack, biTree);biTree = biTree->left;}if (!stackEmpty_Sq(nodeStack)){// 左孩子完毕,则栈顶为最后一个左孩子,进行输出popped = (BinaryTree)malloc(sizeof(BinaryTreeNode));pop_Sq(nodeStack, popped);visit(popped);// 继续迭代右子树的左孩子biTree = popped->right;}}destroyStack_Sq(nodeStack);}
- 按照中序遍历规则,遇到任意非空结点,需要将左子树访问完成才能访问它,所以过程为:
- 压栈;
- 迭代其左孩子。
- 左孩子迭代完成。
- 栈顶元素为该非空结点,出栈,访问它;
- 迭代到其右孩子,作为下一个非空结点的迭代。
- 过程控制
- 同先序遍历一样,非空的控制放到while循环体条件,循环体内不用考虑非空性。
- 根据中序的规则,对结点的访问放到迭代完成其左子树之后。
后序遍历 (左 —> 右 —> 中)
/* 14_二叉树——后序遍历_非递归*/void postOrderTraverse_NonRecur(BinaryTree biTree){if (!biTree){return;}// 存任意非空结点的栈SqStack nodeStack;initStack_Sq(nodeStack);push_Sq(nodeStack, biTree);// 标记前一次访问的结点BinaryTree pre = NULL;while (!stackEmpty_Sq(nodeStack)){// 获取栈顶元素,不出栈,分两种情况讨论getTop_Sq(nodeStack, biTree);/*** 第一大类:* 1. 不存在左右结点;* 2. 前一次访问的结点不为空,且前一次访问的结点【等于当前结点的左孩子】或【右孩子】*/if ((!biTree->left && !biTree->right)|| (pre != NULL&& (pre == biTree->left || biTree == biTree->right))){visit(biTree);BinaryTree bt = NULL;pop_Sq(nodeStack, bt);pre = biTree;}// 第二大类情况,有孩子未被访问,先右后左的优先级入栈其孩子else{// 优先入栈右结点if (biTree->right){push_Sq(nodeStack, biTree->right);}if (biTree->left){push_Sq(nodeStack, biTree->left);}}}}
- 规则:遇到任意一个结点,必须优先访问其左子树,其次访问右子树,最后再访问它本身。
- 难题:对于左右子树的访问,都有访问完成回溯的情况:
- 对于有左右子树的时候,左子树访问完成的回溯,当前结点不能出栈并访问;
- 右子树访问完成,才能进行出栈和访问。
- 需要区分回溯的情况,是从左子树回溯的,还是从右子树回溯的。
- 情况划分:根据这种规则,将遇到一个非空结点的情况划分如下:
- 无左右孩子 –> 可立即访问
- 有孩子,但孩子都访问完成 –> 可立即访问
- 有孩子未被访问。 –> 不可立即访问
- 实现方案:
- 全局设置一个指针,记录上一次被访问的结点。
- 遇到一个结点
- 可立即访问 –>
- 访问它;
- 将栈顶出栈,赋值为上一次遍历的结点;
- 不可立即访问 -> 按优先右子树,再左子树进行压栈,保证左子树的访问在右子树之前。
- 层次遍历(广度优先) ```c / 15_二叉树——层次遍历/ void breadthTraverse(BinaryTree biTree) { if (!biTree) { return; } // 存放子树根结点的队列 CircularQueue cq; initQueue_Cq(cq); enqueue_Cq(cq, biTree); // 保存出队列的元素 BinaryTree deQueued = NULL;
- 可立即访问 –>
while (!queueEmpty_Cq(cq)) { // 任何结点都在出队列时候进行访问。 dequeue_Cq(cq, deQueued); visit(deQueued); if (deQueued->left) {
enqueue_Cq(cq, deQueued->left);
} if (deQueued->right) {
enqueue_Cq(cq, deQueued->right);
} } } ```
首先将根结点入队列,作为迭代的开始。
- 迭代的结点永远从队列出队元素开始。
- 从队列中取出一个结点,访问它,并将它的孩子入队列。
最终队列为空,层次遍历完毕。
- 是否完全二叉树判断
/* 30_二叉树——是否完全二叉树*/bool isCompleteBinary_T(BinaryTree biTree){// 用来标记【只有左孩子】或者【无孩子】bool flag = false;// 空树,直接返回是if (!biTree){return true;}// 保存当前判断结点BinaryTree cur = NULL;// 用循环队列保存下一层待访问结点CQueue cq;initQueue_Cq(cq);enqueue_Cq(cq, biTree);// 队列非空则表示还有结点未被访问while (!queueEmpty_Cq(cq)){dequeue_Cq(cq, cur);if (flag){if ((!cur->rtag && cur->right) || (!cur->ltag && !cur->left)){return false;}}else{// 左右结点都存在if ((!cur->ltag && cur->left) && (!cur->rtag && cur->right)){enqueue_Cq(cq, cur->left);enqueue_Cq(cq, cur->right);}// 只存在右结点,则非完全else if (!cur->rtag && cur->right){return false;}// 对【只有左孩子】,【无孩子】情况,做标记else if (!cur->ltag && cur->left){enqueue_Cq(cq, cur->left);flag = true;}else{flag = true;}}}// 判断到最后都没有中间返回,则它是完全二叉树return true;}
- 是否完全二叉树判断
首先,明确完全二叉树的定义,除了最后一层,其余每层都充满结点,最后一层的结点都集中在左边。
- 完全二叉树按层来判断,则需要参考层次遍历的方式,采用队列数据结构,将当前访问到的结点的孩子加入队列。
- 对是否最后一层的特殊判断,设置一个标记变量flag。
- 若队列当前结点只有左孩子或者没有孩子,标记true。此后出现的结点按完全二叉树定义,应该都没有孩子,若出现了孩子,则不是完全二叉树。
非最后一层。
- 左右孩子都有,则直接入队。
- 只有右孩子,则非完全,直接返回。
- 只有左孩子,按规则,达到最后一层。
- 左孩子入队;
- 标记置为true;
- 无孩子,也是最后一层,标记置为true。
- 叶子结点个数
/* 16_二叉树——叶子个数*/int leafCount_T(BinaryTree biTree){// 遇到空结点,则个数不变if (!biTree){return 0;}// 没有左右孩子,则它是叶子结点else if (!biTree->left && !biTree->right){return 1;}// 否则,求它的子树的叶子结点个数else{return leafCount_T(biTree->left) + leafCount_T(biTree->right);}}
- 叶子结点个数
当前为空结点,则个数增加 0;
- 当前非空,无左右孩子,则个数增加 1;
当前非空,有孩子,则叶子个数为其左孩子叶子个数 + 右孩子叶子个数。
- 第 k 层的结点个数
/* 17_二叉树——第k层结点数目*/int getKLevel_T(BinaryTree biTree, int k){// 以根结点开始的第 k 层 => 以根结点的子孩子开始的第 k-1 层if (!biTree){return 0;}// 递归结束条件:1即为当前层级,以当前结点为开始的第一层,即当前根结点,只有1个if (k == 1){return 1;}return getKLevel_T(biTree->left, k - 1) + getKLevel_T(biTree->right, k - 1);}
- 第 k 层的结点个数
以根结点开始的第k层 => 以根结点的孩子开始的第 k - 1层。
注意控制递归终止条件。
- 两个二叉树结构是否相同 ```c / 18_二叉树——结构是否相同/ bool structureCompare_T(BinaryTree bt1, BinaryTree bt2) { /**
- 总的思路是,遇到不同的即返回false,否则一直比较,比较完成返回true */ // 到最终两个一样为空 if (!bt1 && !bt2) { return true; } // 当一个为空,另一个不为空的时候 else if ( (!bt1 && bt2) || (!bt2 && bt1) ) { return false; } // 都不为空,则比较其孩子 bool same = structureCompare_T(bt1->left, bt2->left); same = same && structureCompare_T(bt1->right, bt2->right); return same; } ```
等价于比较结点有或没有的情况。
- 遇到一个有另一个没有的情况返回false。
- 比较到最后都相同则返回true。
- 求一个二叉树的镜像
/* 19_二叉树——求镜像*/void treeMirror_T(BinaryTree biTree){// 左右孩子互换,从上到下if (!biTree){return;}// 先交换左右孩子根结点BinaryTree temp = biTree->left;biTree->left = biTree->right;biTree->right = temp;// 再对左右孩子分别进行互换treeMirror_T(biTree->left);treeMirror_T(biTree->right);}
- 求一个二叉树的镜像
求两个结点的最低公共祖先结点
- 首先确定计算参数,在一个树中求两个结点的最低公共祖先结点。入参为指向确定树的根结点的指针和指向两个结点的指针。
- 可能的情况有
- 直系关系。一个结点直接是另一个结点的直系祖先。
- 旁系关系。两个结点没有直接继承关系。
算法描述。
/* 21_二叉树——找最低公共祖先*/BinaryTree findLCA_T(BinaryTree biTree, BinaryTree bt1, BinaryTree bt2){// 首先对当前根结点进行判断// 如果当前根结点为空,或是等于两个待判断结点中的任意一个,则当前根结点即是最低公共祖先if (!biTree){// 这个空结果,影响下面递归的判断return NULL;}if (biTree == bt1 || biTree == bt2){return biTree;}// 否则分别在根结点的左右子树进行查找,两边都有一个结果,可能为空BinaryTree left = findLCA_T(biTree->left, bt1, bt2);BinaryTree right = findLCA_T(biTree->right, bt1, bt2);// 分别在当前根结点结点两边if (left && right){return biTree;}// 在其中一边,取非空的一边return left ? left : right;}
- 运用递归的思想,即可以先求出两个结点对于当前根结点的左右子树的关系。
- 两个结点对左子树和右子树都有关系。
- 那么此时的根结点即是两个结点的最低公共祖先。
- 两个结点都只与左子树或右子树有关系。
- 那么即是求所在的子树和两个结点的关联关关系。
- 两个结点对左子树和右子树都有关系。
- 递归终止条件控制
- 当前根结点为空,则所求的最低公共祖先不存在,为空。
- 当前根结点等于结点中的一个,那么当前结点即是所求的最低公共祖先结点。
二叉树任意两个结点的距离 ```c / 22_二叉树——结点距离/ int nodeDistance_T(BinaryTree biTree, BinaryTree bt1, BinaryTree bt2) { // 先找到最低公共父结点 BinaryTree lca = findLCA_T(biTree, bt1, bt2);
// 再求出LCA结点到两个结点距离,求和 int left = levelDist_T(lca, bt1); int right = levelDist_T(lca, bt2);
return left + right; }
/ 23_二叉树——结点相隔层数/ int levelDist_T(BinaryTree biTree, BinaryTree bt) { // 用 -1 标识没找到 if (!biTree) { return -1; } // 找到了,当前层,层数不变 if (biTree == bt) { return 0; }
// LCA结点和目标结点是直系关系。从LCA结点往下找int levelDist = levelDist_T(biTree->left, bt);// 若左子树没有找到,则找右子树if (levelDist == -1){levelDist = levelDist_T(biTree->right, bt);}// 找到了,则回溯if (levelDist != -1){return levelDist + 1;}// 左右子树都没找到return -1;
}
- 等价于**LCA结点**到两个结点的距离**(两个直系距离)之和**,其中每隔一个父子层级关系,距离为 1 。- LCA结点与目标结点的直系距离,则需要运用递归思想,从LCA结点向下找目标结点。- 迭代的结点是第一个参数(当前根结点)- 如果左子树找不到,则找右子树- 找到之后需要回溯,加上当前的层级距离为 1。- 结点的所有祖先```c/* 24_二叉树——结点所有祖先*/bool allAncestors_T(BinaryTree biTree, BinaryTree bt){// 利用求两个直系结点距离的思路// 如果到最叶子结点都没有找到,则返回false,找到则返回trueif (!biTree){return false;}if (biTree == bt){return true;}// 从左右子树找if (allAncestors_T(biTree->left, bt) || allAncestors_T(biTree->right, bt)){// 找到时候访问,并进行回溯visit(biTree);return true;}// 左右子树都每找到return false;}
- 可以参考两个结点的直系距离的思路。实际也是递归,从上往下找的过程。
- 在回溯的时候对父结点进行访问,则回溯到根结点,所有的祖先已经被访问到了。
线索化二叉树
中序线索化及遍历
中序线索化 ```c / 26_二叉树——中序线索化/ void inThreading_T(BinaryTree& bt, BinaryTree& pre) { if (!bt) { return; } if (!bt->ltag) { inThreading_T(bt->left, pre); }
// 进行中序的线索化操作 // 遇到左孩子为空,即赋值为前置 if (!bt->left || bt->ltag) { bt->ltag = true; bt->left = pre; } // 若前置结点非空,且没有右孩子 if (pre && (!pre->right || pre->rtag)) { pre->rtag = true; pre->right = bt; } // 当前结点 => 下一次迭代的前置结点 pre = bt;
if (!bt->rtag) { inThreading_T(bt->right, pre); } }
- 线索化利用了中序递归遍历的逻辑,将对结点的访问改为线索连接的过程。- 线索连接,在两个参数的基础上做递归:- 当前结点- 前一个被访问的结点- 线索连接过程要点<br />* 仅对**非线索指针**进行线索化,否则造成死循环。<br />* **当前连接前驱**。当前结点,左孩子为空,则置为前驱线索,指向前驱;<br />* **前驱连接当前**。若前驱节点的右孩子为空,则将当前结点置为其前驱的后继(需判断第一个结点,前驱为空的情况)<br />* **迭代pre变量**。线索连接完成,当前结点迭代为下一次访问的前驱。<br />* 为了兼容**多次线索**或**多种线索**的过程。增加对**当前结点左标记**与**前驱结点右标记**的判断- 中序线索遍历```c/* 29_二叉树——中序线索遍历*/void inThreadTraverse_T(BinaryTree biTree){if (!biTree){return;}// 迭代的变量,保存当前及其上一次的结点BinaryTree cur = biTree;// 结点为空则迭代结束(线索作用)while (cur){// 找到从根节点开始的左子树的叶子结点【中序第一个结点】while (cur->left && !cur->ltag){cur = cur->left;}visit(cur);// 若结点没有右子树,只有后继,则直接输出它while (cur->rtag){visit(cur->right);cur = cur->right;}// 有右子树,则按照中序遍历规则,必须先访问完成【右子树根结点的左子树 cur->right-> left】才能访问【右子树的根结点 cur->right】// 迭代其右子树,重新进入上面的逻辑cur = cur->right;}}
- 按照中序的规则,优先访问完成左子树。所以每遇到一个结点,先找到**左子树的最左叶子**。- 对于结点右孩子的访问情况- 节点的**右孩子**,在**遍历完成之前的迭代过程**都是**非空**的(线索的作用)- 区分结点**右孩子**作为**线索**和**子树**的区别。- **作为线索**,则该线索指向的结点的左子树是不能再被访问的(**当前结点**即是从**线索指向结点的左孩子**迭代下来的)- **作为子树**,则按中序规则,序优先迭代左子树,即回到主循环中。
前序线索化及遍历
前序线索化
/* 25_二叉树——前序线索化*/void preThreading_T(BinaryTree& bt, BinaryTree& pre){if (!bt){return;}// 进行前序线索化if (!bt->left || bt->ltag){bt->ltag = true;bt->left = pre;}if (pre && (!pre->right || pre->rtag)){pre->rtag = true;pre->right = bt;}pre = bt;// 孩子不作为线索,才执行if (!bt->ltag){preThreading_T(bt->left, pre);}if (!bt->rtag){preThreading_T(bt->right, pre);}}
- 利用前序递归遍历的逻辑,将访问过程改为线索化过程。
- 主逻辑同中序线索化,同样方法兼容多种和多次线索的过程。
- 只对非线索指向的结点进行线索化,避免死循环。
前序线索遍历
/* 28_二叉树——前序线索遍历*/void preThreadTraverse_T(BinaryTree biTree){if (!biTree){return;}// 迭代的变量BinaryTree cur = biTree;// 结点为空则代表结束while (cur){visit(cur);// 优先访问当前结点while (cur->left && !cur->ltag){cur = cur->left;visit(cur);}cur = cur->right;}}
- 按前序遍历的思路,优先访问根结点。
- 顺着线索访问即可,不用关注右结点是子树还是线索。
- 后序线索化及遍历
- 后序线索化逻辑同前序和中序一致。
- 由于后序线索化对遍历的帮助不大,所以不再纠结于后序的线索遍历。

