08_多路查找树

二叉树的劣势

• 当结点数量过多时（海量，如1亿），二叉树会出现如下问题：

  • 构建二叉树，需要进行多次IO操作。
    • 结点数量较多会导致多次I/O来获取结点。
  • 二叉树的高度会很大，降低操作速度。

    多叉树

• 通过重新组织结点，以降低树的高度。

• 多叉树允许一个结点有多个子结点，比如2-3树，2-3-4树。

一、B树

1. 基本概念

是一种多路平衡查找树。对于m阶B树。

• 每个节点最多**m-1个关键字，最多m个子结点**。

• 根节点最少可以只有1个**关键字。根节点的关键字**数量范围：1 <= k <= m-1
• 非根节点至少有m/2个关键字。非根节点的关键字数量范围：m/2 <= k <= m-1。
• 每个节点中的关键字都按照从小到大**的顺序排列**。
• 叶子节点都位于同一层（根到所有叶子的高度相同）。

B树_索引、数据、指针的关系

2. 插入

1) 规则

• 判断当前结点key的个数是否小于等于m-1。
  • 如果满足，直接插入。
  • 如果不满足，将节点的中间的key将这个节点分为左右两部分，中间的节点放到父节点中即可。

2) 模拟（5阶B树）

3. 删除

• 相对于插入操作来说，稍微复杂。

  1) 规则

• 判断删除后结点数是否**大于 m / 2**。

  • 满足，直接删除。
  • 不满足。
    • 借了之后兄弟结点的结点，兄弟仍满足。则【父结点 -> 当前结点】【兄弟结点 -> 父结点】转移。
    • 借了兄弟结点，兄弟不满足。则【父结点 -> 当前结点】【兄弟结点 -> 父结点】，并且与兄弟结点合并。

      2) 模拟（5阶B树）

      

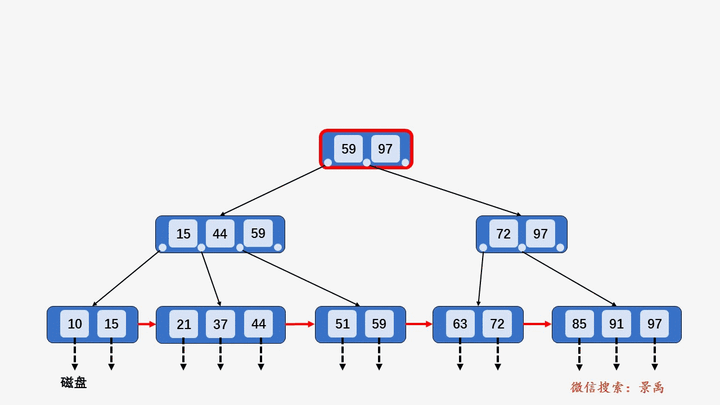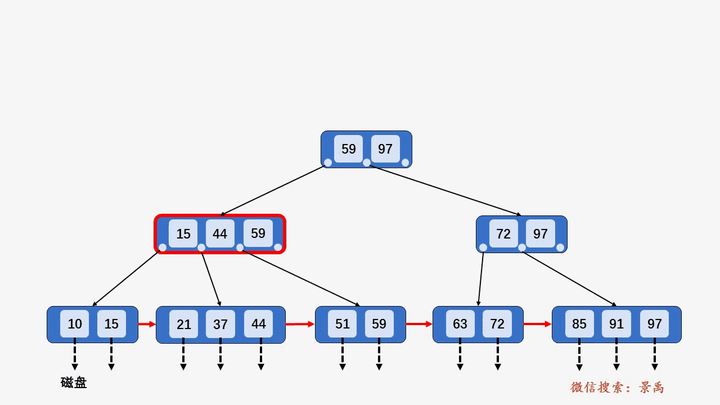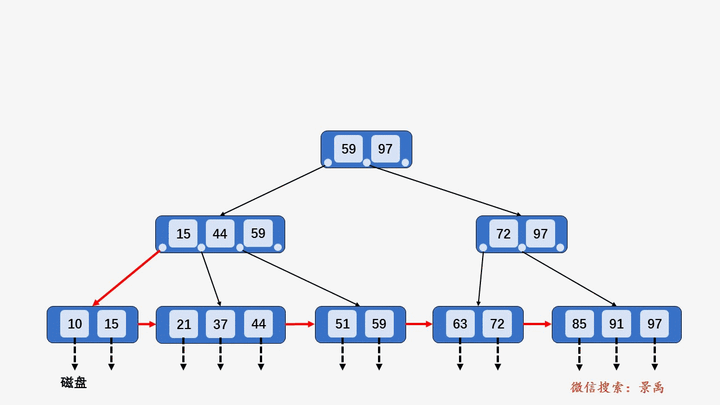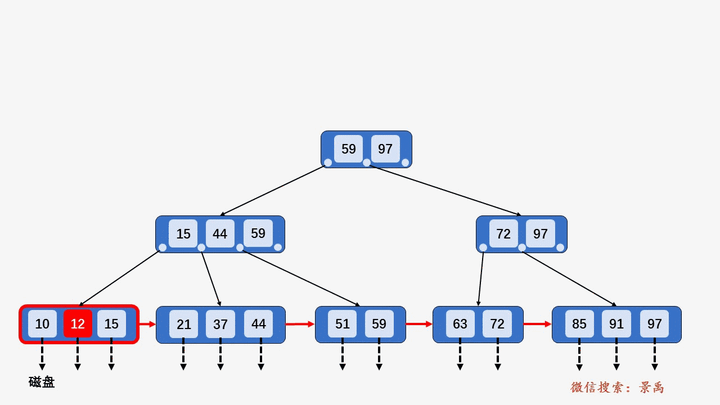
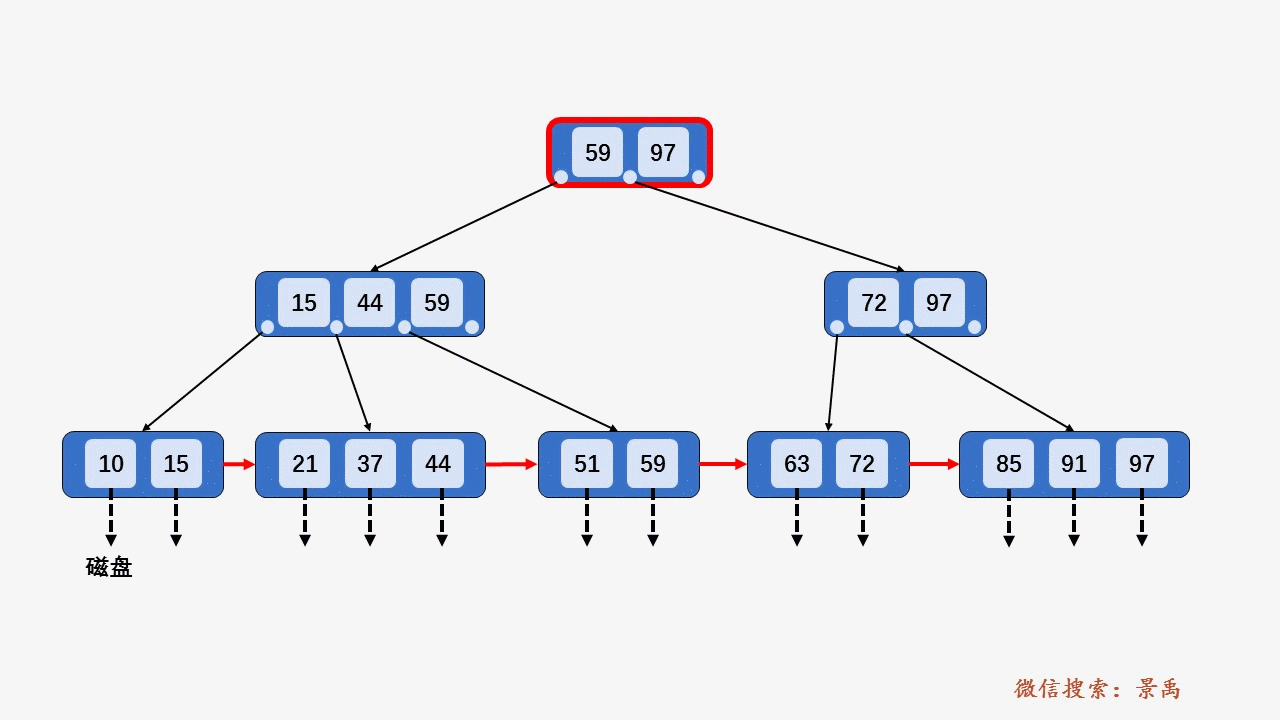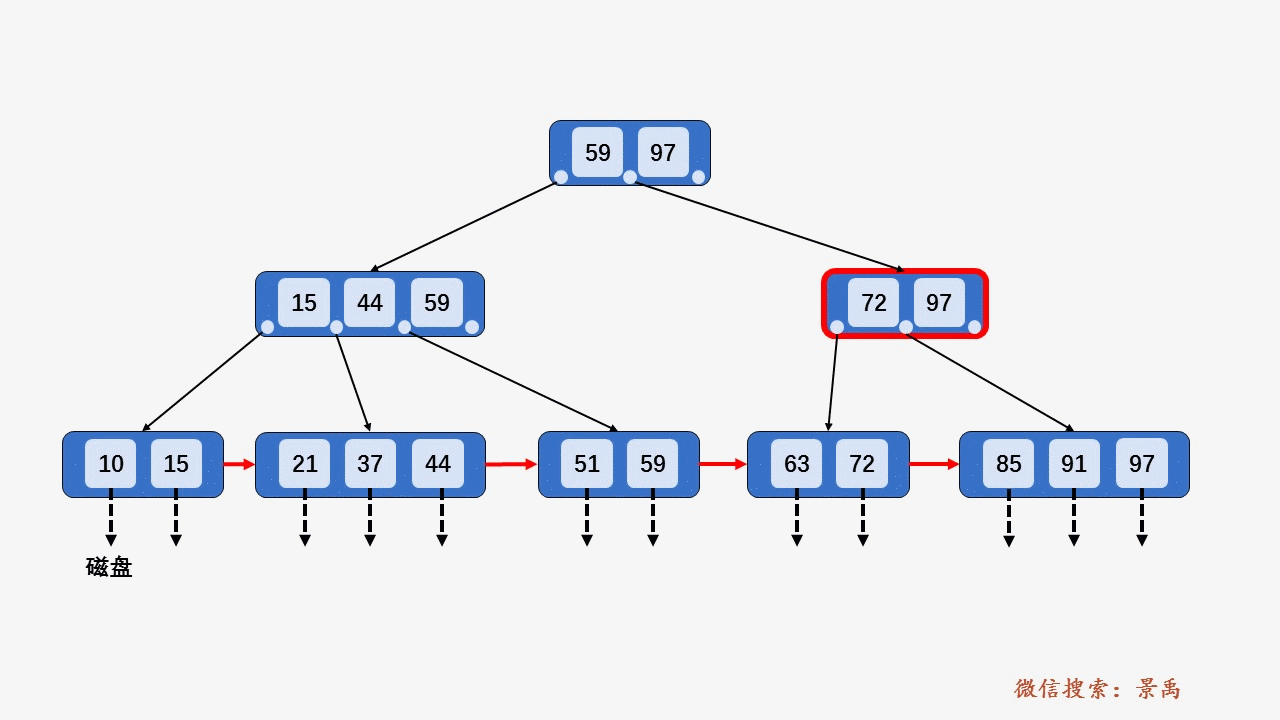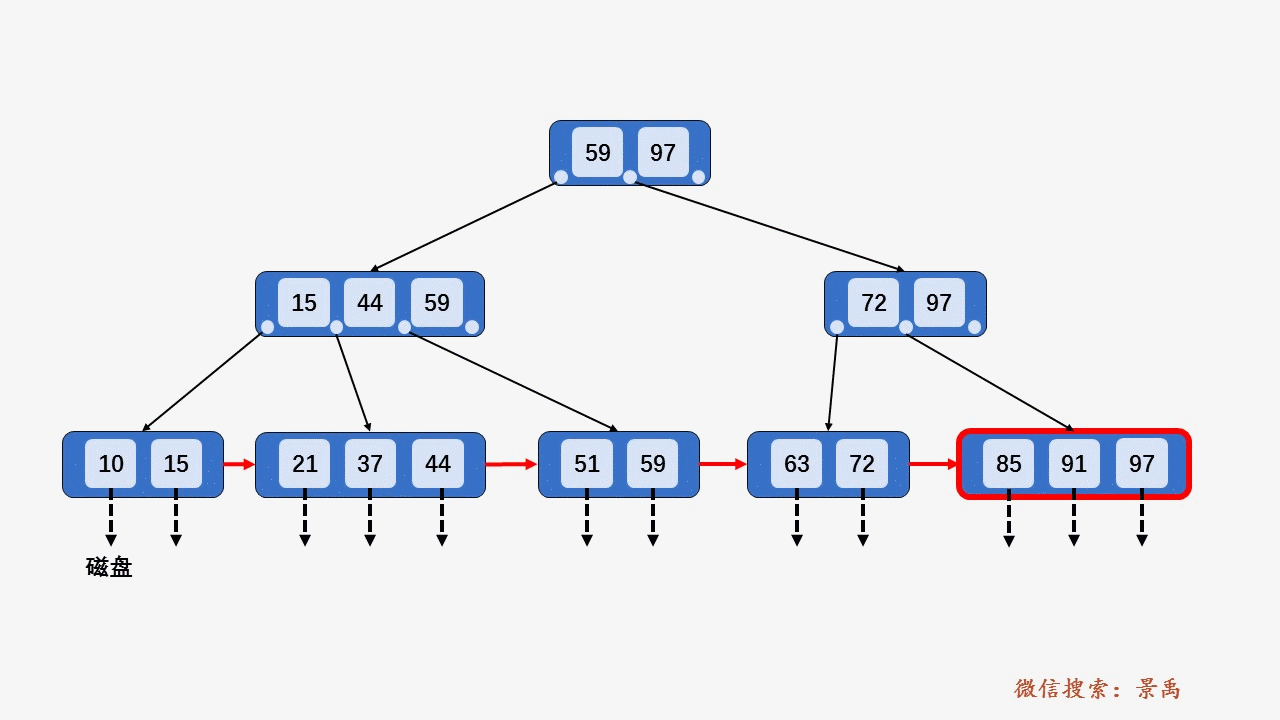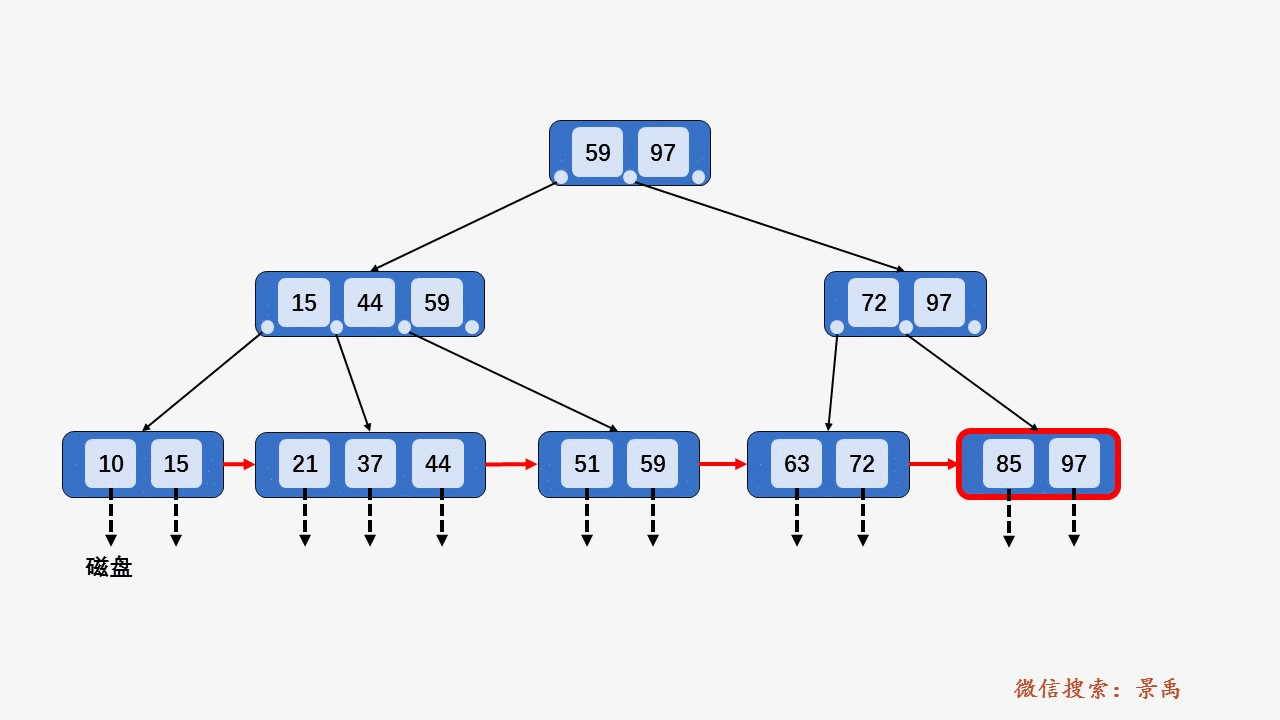
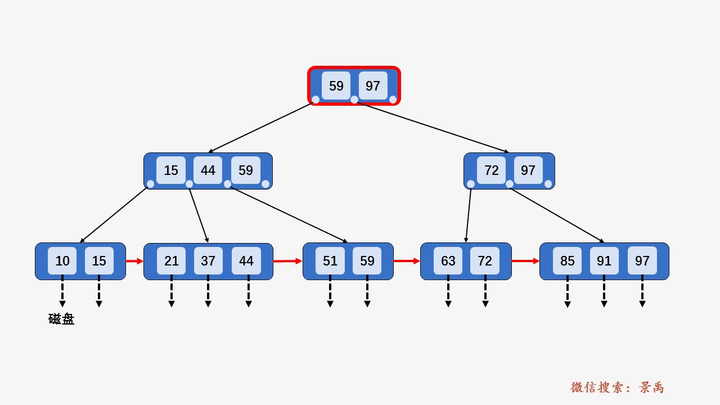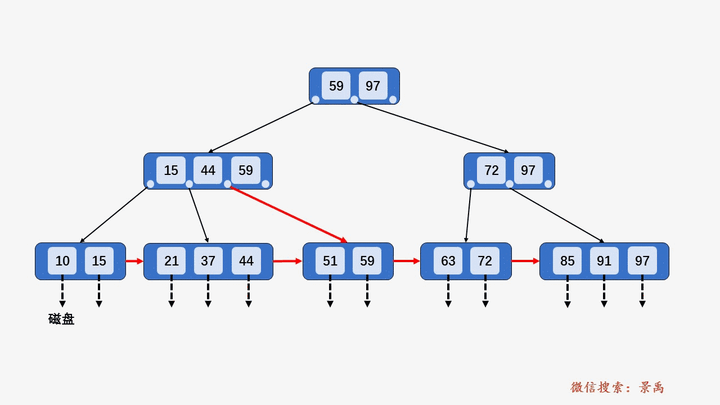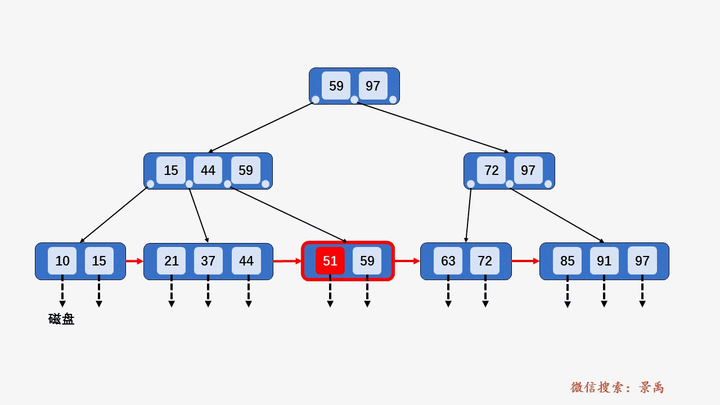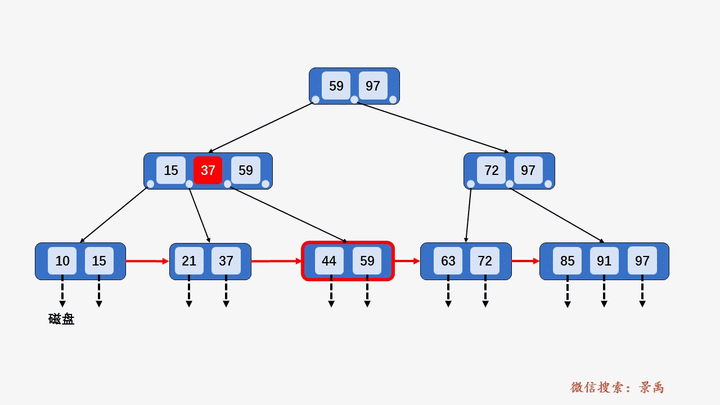
二、B+树

1. 概述

在B树基础上做了优化。

• 每个结点可以包含更多的元素结点。
  • 为了降低树的高度。
  • 将数据变为更多区间，区间越多，数据检索越快。
• 非叶子结点仅存储key值，叶子结点存储key值和数据。
• 叶子结点通过指针互相连接。

2. InnoDB引擎的的B+树索引

• 聚簇索引：索引和数据存放于同一个文件

3. MyISAM引擎的B+树索引

• 非聚簇索引：索引和数据分开存放，索引存在于myi文件，数据存在于myd文件

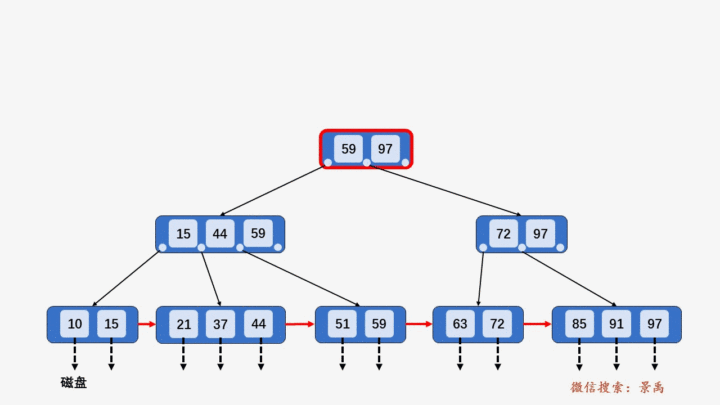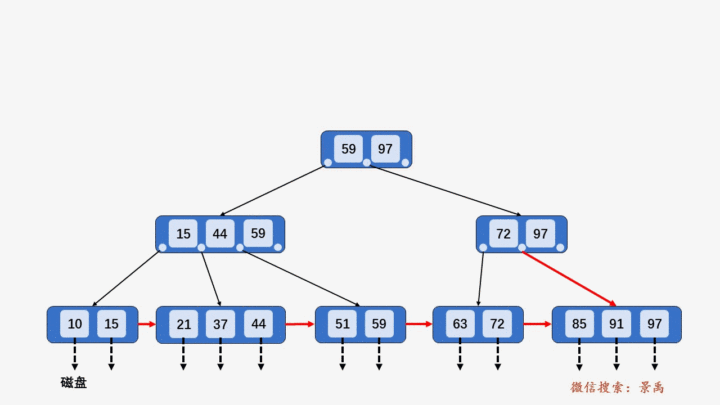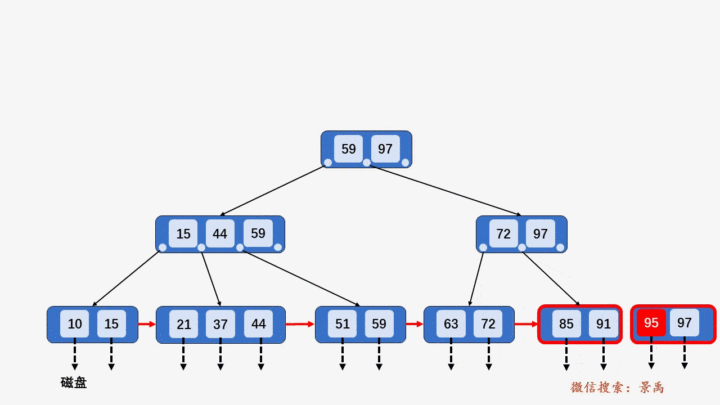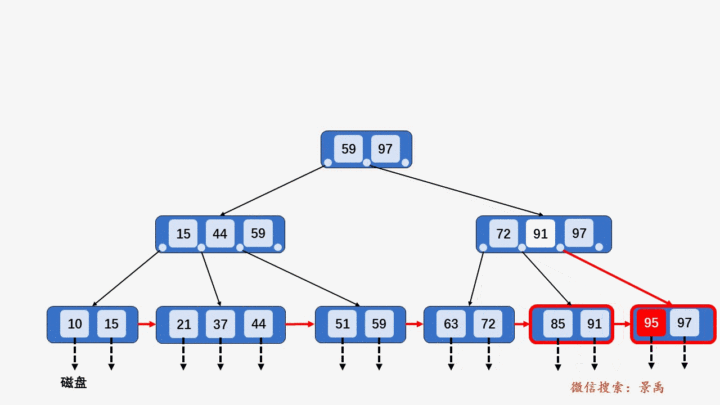
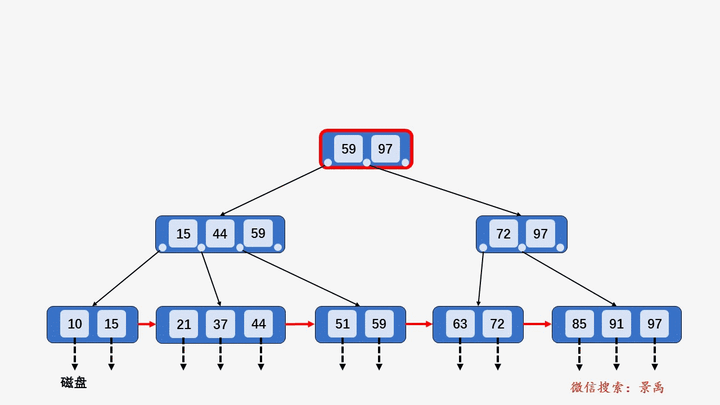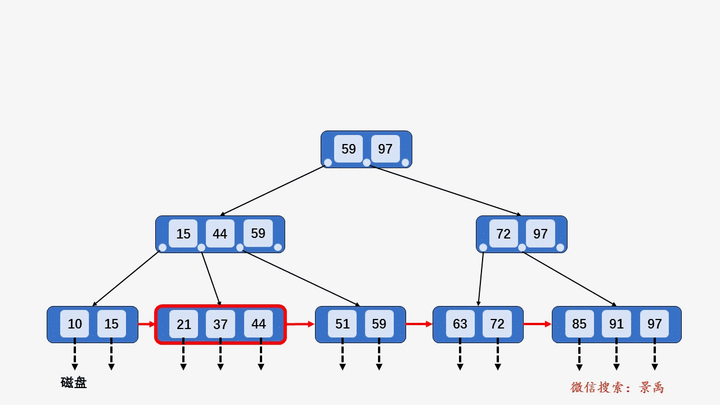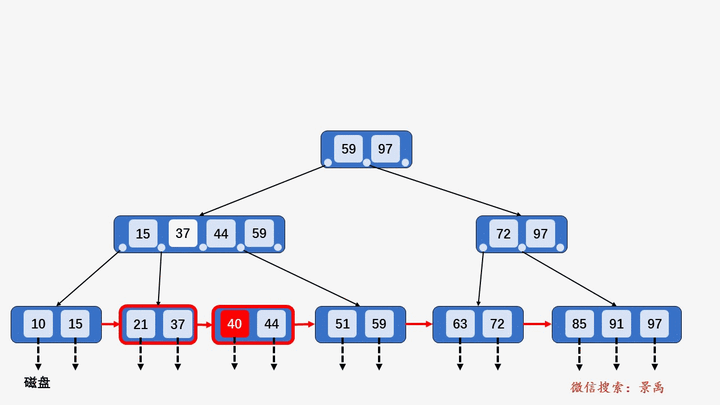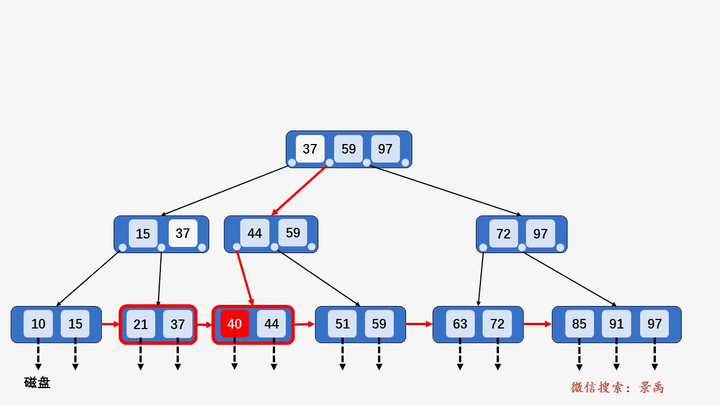
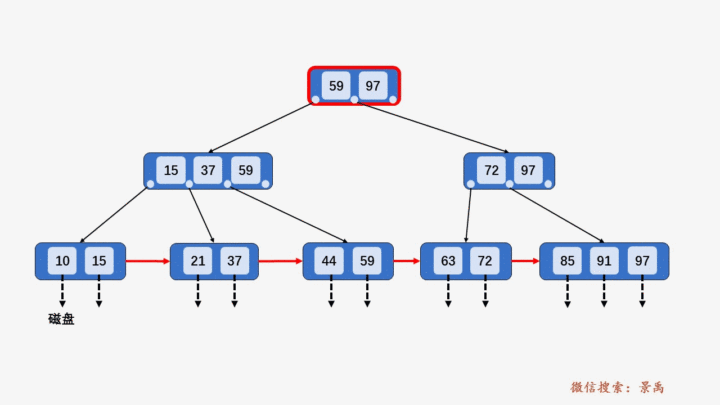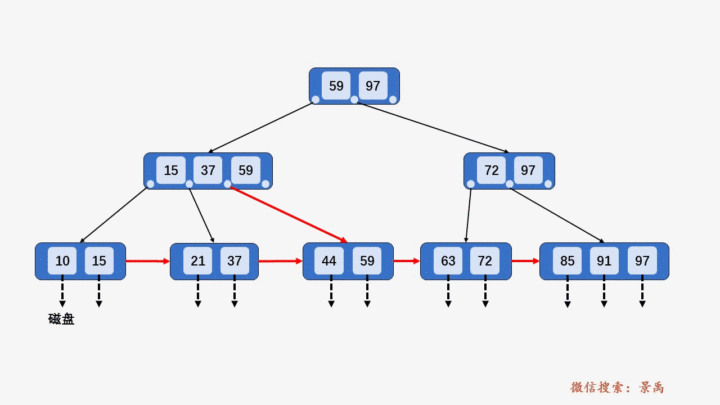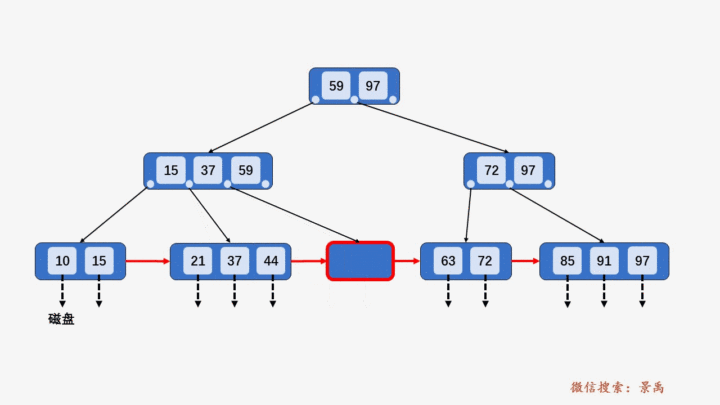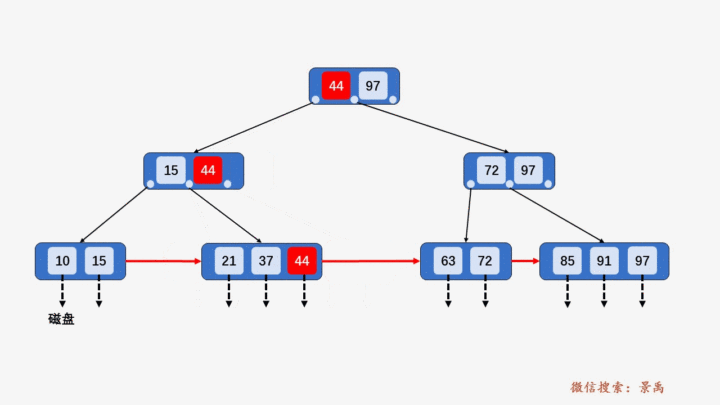
4. B+树插入元素

• 插入元素全部在叶子结点进行，不能破环关键字自小而大的顺序。
• 插入过程超过树的阶数需要分裂。

1) 含有关键字数目小于阶数 M，则直接插入。

2) 含有关键字数目等于阶数 M，则需要将该结点分裂为两个结点，一个结点包含 ⌊M/2⌋ 个元素，另一个结点包含 ⌈M/2⌉ 个元素。同时，将⌈M/2⌉的关键字上移至其双亲结点。

3) 上移操作导致其双亲结点中关键字个数大于 M，则应继续分裂其双亲结点。

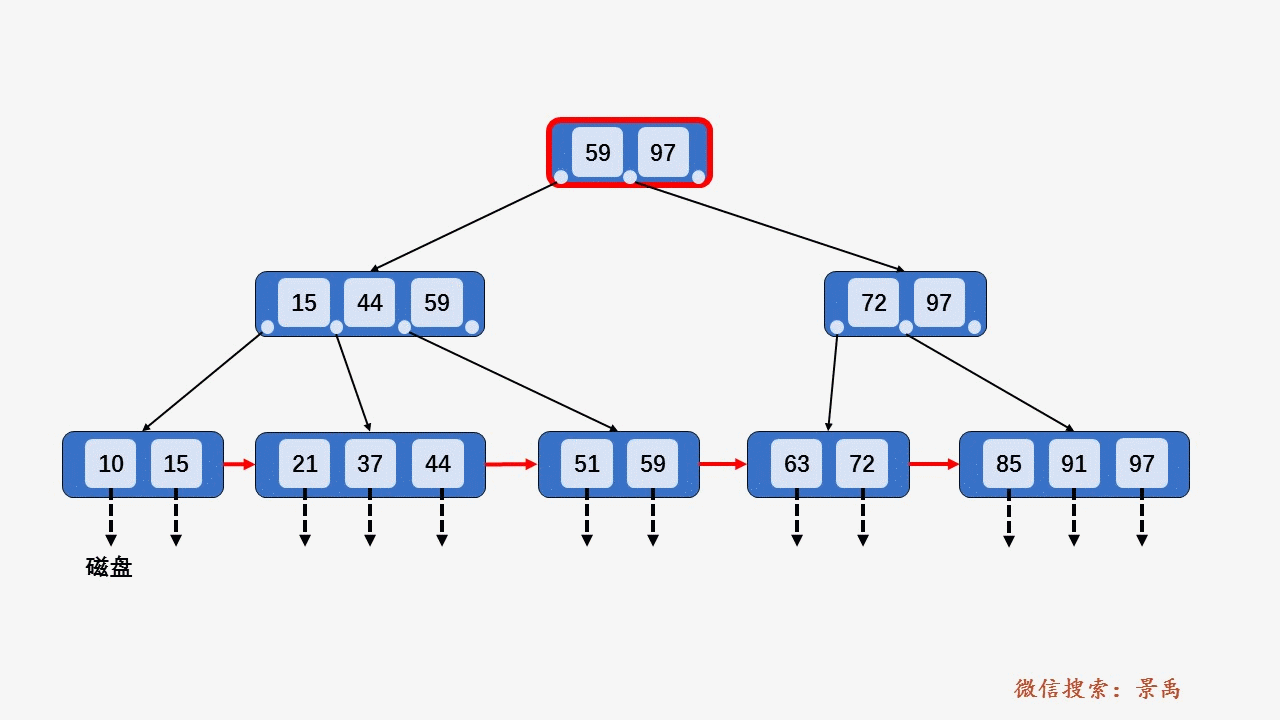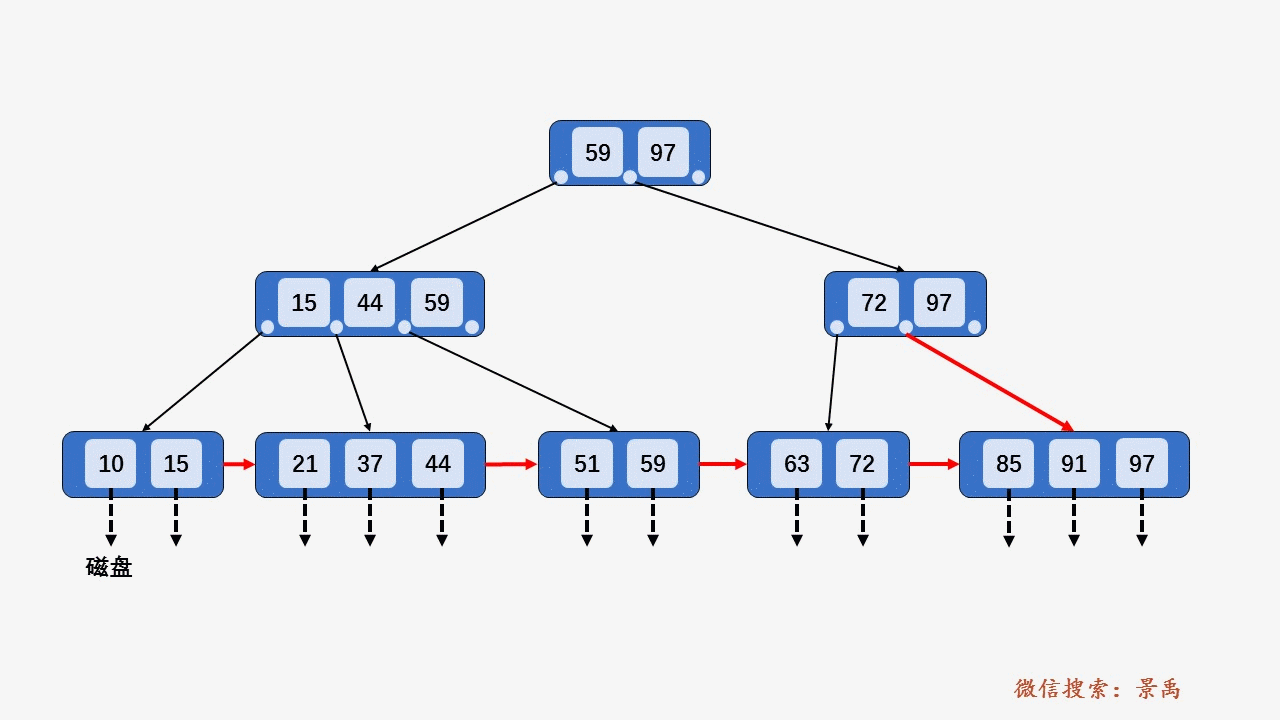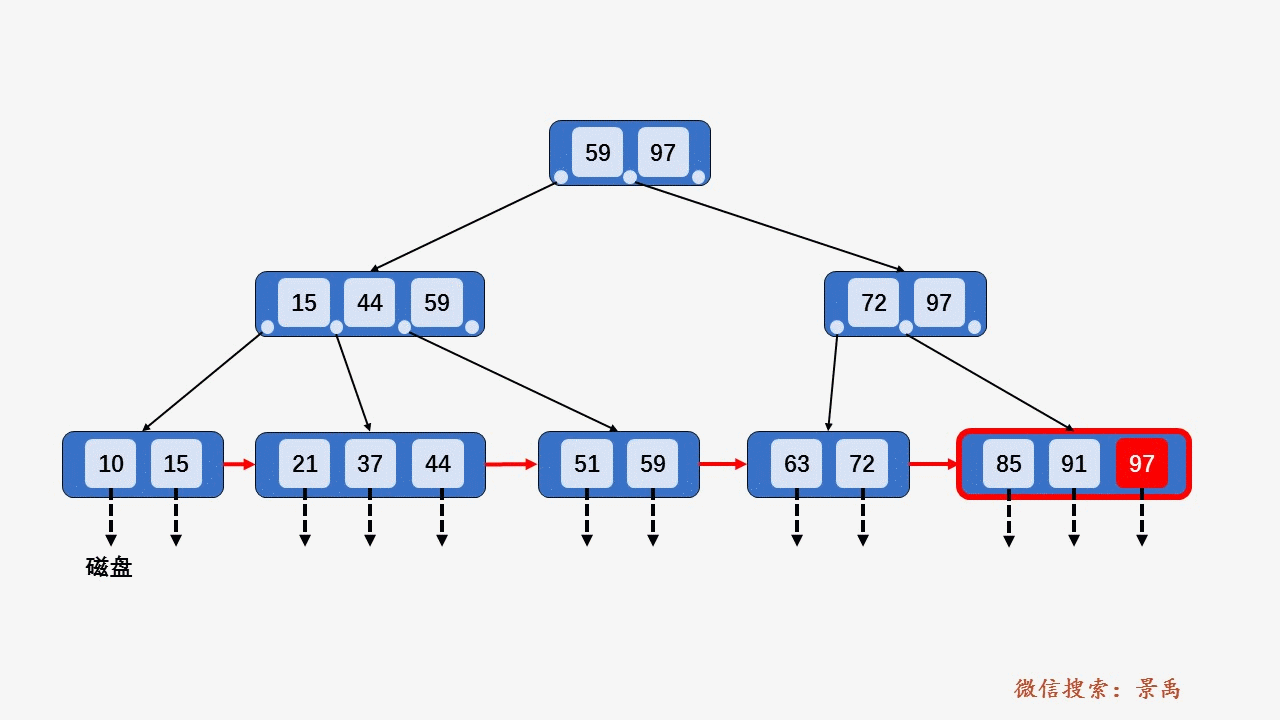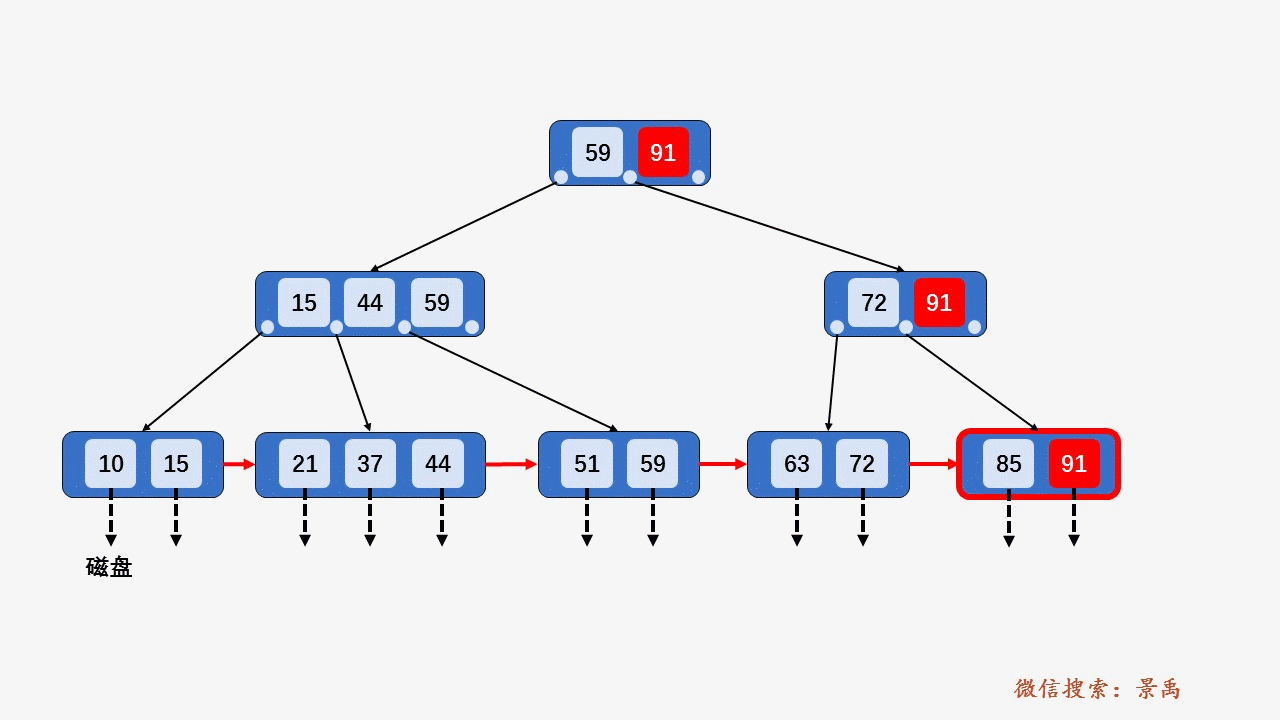
4) 关键字比当前结点中的最大值还大，破坏了B+树中从根结点到当前结点的所有索引值，此时需要及时修正后，再做其他操作。

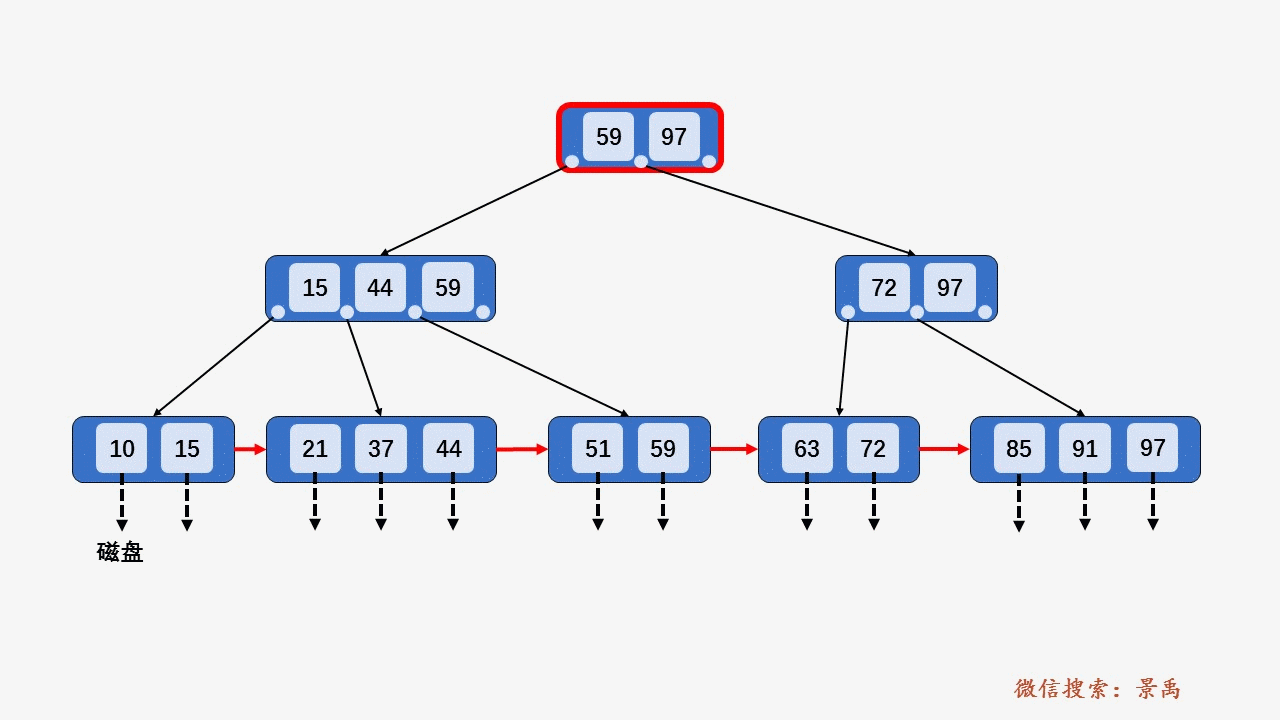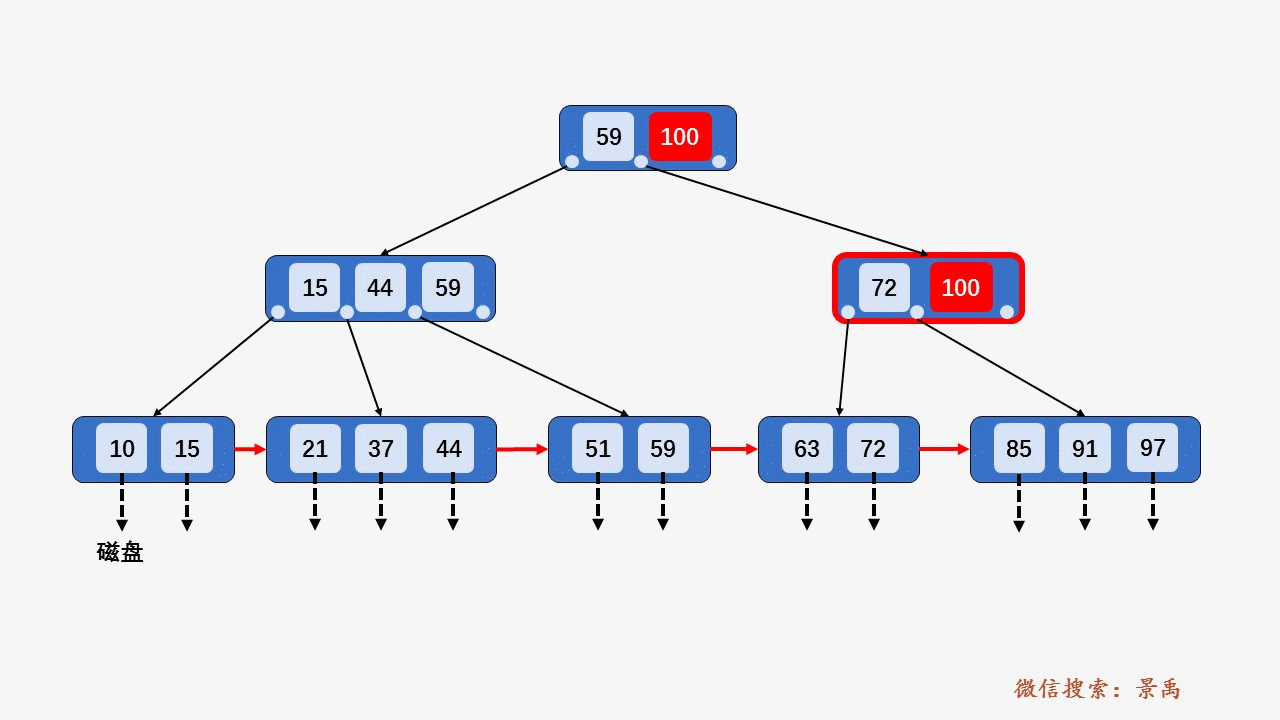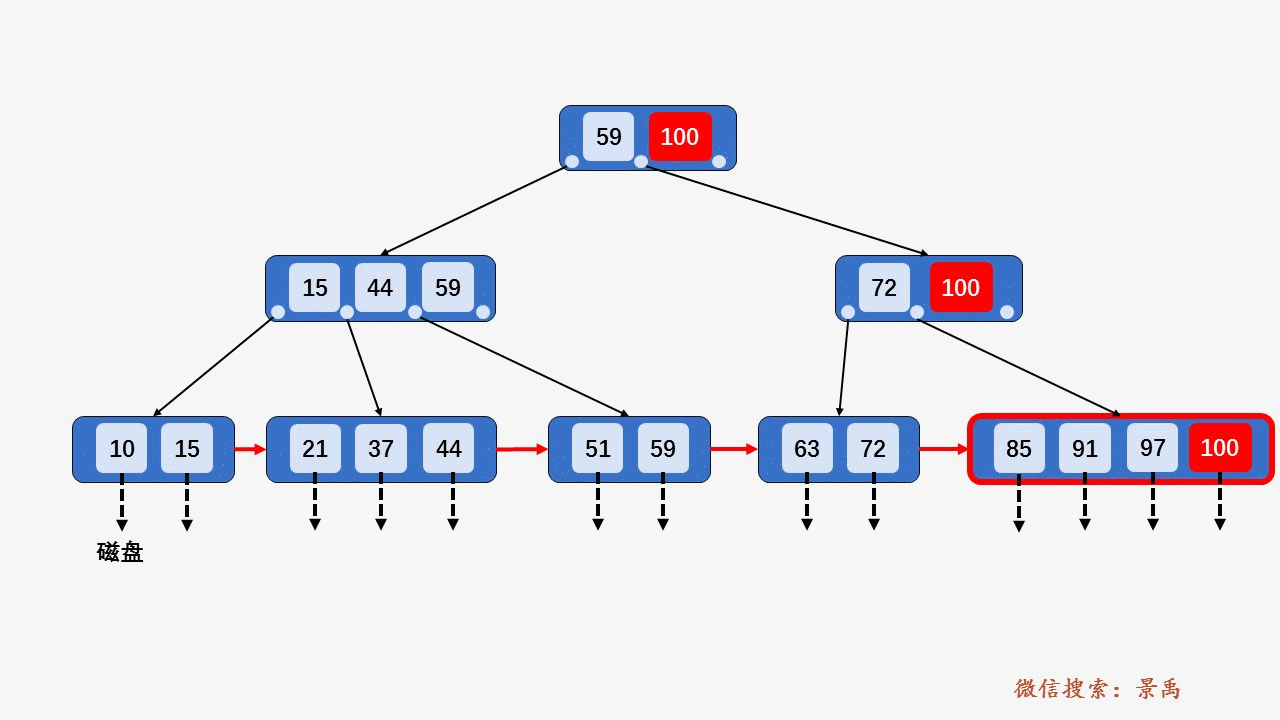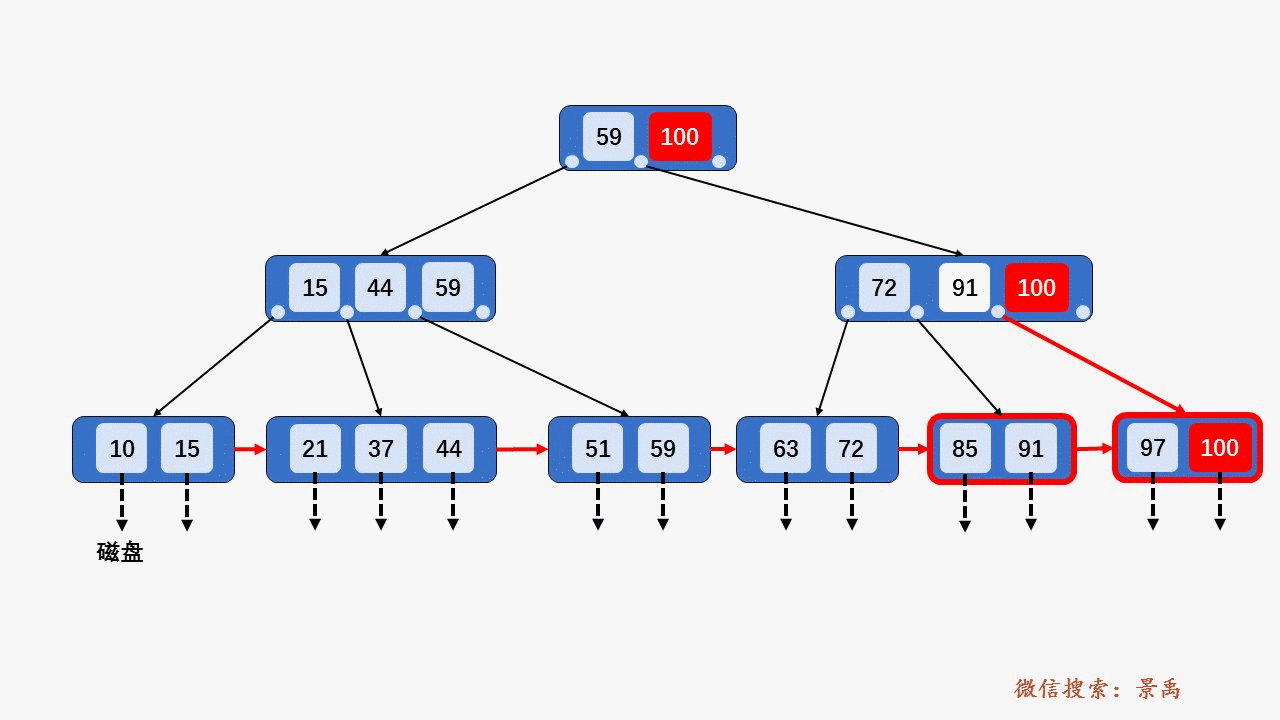
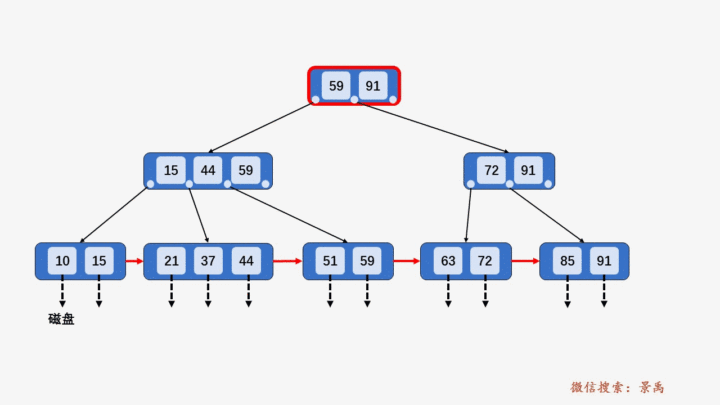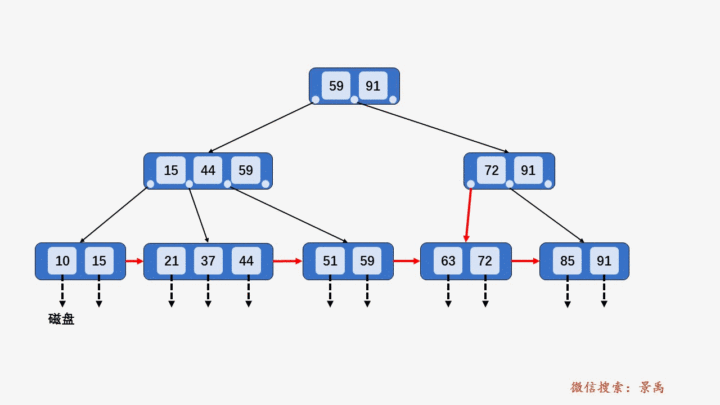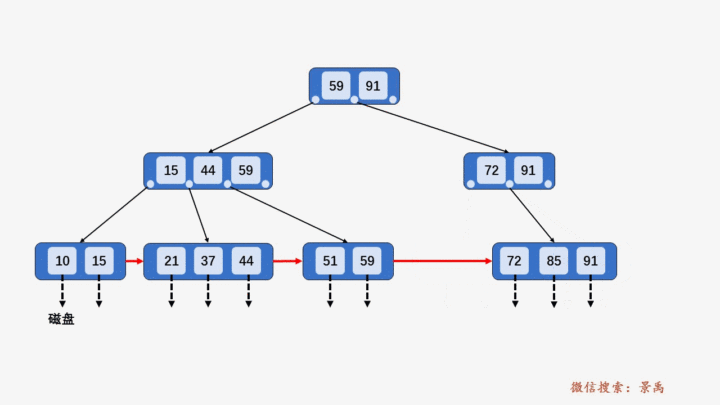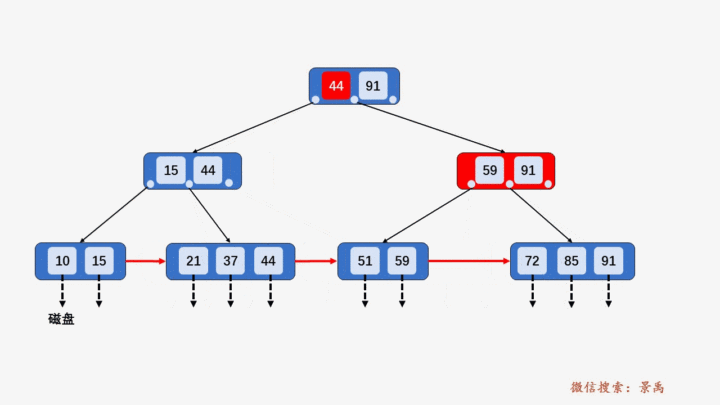
5. B+树删除元素

1) 待删除结点，关键字个数大于⌈M/2⌉，做删除操作不会破坏 B+树规则，则可以直接删除。

2) 删除某结点中最大或者最小的关键字，就会涉及到更改其双亲结点一直到根结点中所有索引值的更改。

3) 导致当前结点中关键字个数小于 ⌈M/2⌉，若其兄弟结点中含有多余的关键字，可以从兄弟结点中借关键字完成删除操作。

4) 导致当前结点中关键字个数小于 ⌈M/2⌉，兄弟结点没有多余的关键字，需要和兄弟结点合并。

5) 因合并使其双亲结点破坏 B+树的结构，需要依照以上规律处理其双亲结点。