合并两个有序链表

将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例：
输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

解法

同上两种思路一个是递归，一个是遍历。分别用 Java 和 c++ 写的。
递归： 新建个链表，每次两个链表当中选一个小值复制过去，那么现在是不是就是合并两个链表（其中有一个已经赋值过去了，就是之前的 .next，然后递归就可以了。
遍历：
新建一个链表，我们先把第一个值复制过去，然后当两个链表都存在的时候，谁值小就把谁链接到新链表后面然后后移一个，直到两个当中某一个为空了，最后把两个链表剩余的直接链接上去就可以了。

AC代码

  1. /**
  2. * Definition for singly-linked list.
  3. * struct ListNode {
  4. *     int val;
  5. *     ListNode *next;
  6. *     ListNode(int x) : val(x), next(NULL) {}
  7. * };
  8. */
  9. class Solution {
  10. public:
  11.    ListNode* mergeTwoLists(ListNode* pHead1, ListNode* pHead2) {
  12.    ListNode *pHead = new ListNode(0);
  13.    ListNode *p = pHead;
  14.    while(pHead1 != NULL && pHead2 != NULL)
  15.    {
  16.        if(pHead1->val < pHead2->val)
  17.        {
  18.            p->next = pHead1;
  19.            pHead1 = pHead1->next;
  20.        }
  21.        else
  22.        {
  23.            p->next = pHead2;
  24.            pHead2 = pHead2->next;
  25.        }
  26.        p = p->next;
  27.    }
  28.    if(pHead1 != NULL)
  29.    {
  30.        p->next = pHead1;
  31.        pHead1=pHead1->next;
  32.        p=p->next;
  33.    }
  34.    if(pHead2 != NULL)
  35.    {
  36.        p->next = pHead2;
  37.        pHead2=pHead2->next;
  38.        p=p->next;
  39.    }
  40.    return pHead->next;
  41.    }
  42. };

反转链表

反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL

解法

递归，先反转从第二个结点到最后一个结点的链表，然后再将头结点放到已反转链表的最后，函数返回新链表的头结点。

AC代码

  1. /**
  2. * Definition for singly-linked list.
  3. * struct ListNode {
  4. *     int val;
  5. *     ListNode *next;
  6. *     ListNode(int x) : val(x), next(NULL) {}
  7. * };
  8. */
  9. class Solution {
  10. public:
  11.    ListNode* reverseList(ListNode* head) {
  12.        ListNode *ans=NULL;
  13.        ListNode *pre=NULL;
  14.        ListNode *temp=head;
  15.        // 不断取出和向后移动头节点
  16.        // 并将头节点连接到新头节点后面
  17.        while(temp!=NULL)
  18.        {
  19.            ListNode *nextt=temp->next;
  20.            if(nextt==NULL)
  21.                ans=temp;
  22.            temp->next=pre;
  23.            pre=temp;
  24.            temp=nextt;
  25.        }
  26.        return ans;
  27.    }
  28. };

两数相加

给出两个 非空 的链表用来表示两个非负的整数。其中，它们各自的位数是按照 逆序 的方式存储的，并且它们的每个节点只能存储 一位 数字。
如果，我们将这两个数相加起来，则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外，这两个数都不会以 0 开头。
示例：
输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

解法

按我们的正常的加法来进行运算，但是要保存进位。

AC代码

  1. /**
  2. * Definition for singly-linked list.
  3. * public class ListNode {
  4. *     int val;
  5. *     ListNode next;
  6. *     ListNode(int x) { val = x; }
  7. * }
  8. */
  9. public class Solution {
  10.    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
  11.        ListNode l3 = new ListNode(0);
  12.        ListNode res = l3;
  13.        int value = 0;
  14.        int flag = 0;
  15.        while (l1 != null || l2 != null || flag == 1) {
  16.            int sum = flag;
  17.            sum += (l1 != null ? l1.val : 0) + (l2 != null ? l2.val : 0);
  18.            l1 = (l1 != null ? l1.next : null);
  19.            l2 = (l2 != null ? l2.next : null);
  20.            l3.next = new ListNode(sum % 10);
  21.            flag = sum / 10;
  22.            l3 = l3.next;
  23.        }
  24.        return res.next;
  25.    }
  26. }

排序链表

在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序。
示例 1:
输入: 4->2->1->3
输出: 1->2->3->4
示例 2:
输入: -1->5->3->4->0
输出: -1->0->3->4->5

解法

利用之前学习的排序算法来写即可

AC代码

  1. /**
  2. * Definition for singly-linked list.
  3. * struct ListNode {
  4. *     int val;
  5. *     ListNode *next;
  6. *     ListNode(int x) : val(x), next(NULL) {}
  7. * };
  8. */
  9. class Solution {
  10. public:
  11.    ListNode* sortList(ListNode* head) {
  12.        if (head == NULL || head->next == NULL) {
  13.            return head;
  14.        }
  15.        return mergeSort(head);//去掉链表尾端的寻找
  16.    }
  17.    ListNode* mergeSort(ListNode* head) {
  18.        if (head == NULL || head ->next == NULL) {//这段链表只有一个节点
  19.            return head;
  20.        }
  21.        //快慢指针，定位链表中间
  22.        ListNode *slowPtr = head, *fastPtr = head->next;
  23.        while (fastPtr != NULL && fastPtr->next != NULL) {
  24.            slowPtr = slowPtr->next;//慢指针走一步
  25.            fastPtr = fastPtr->next;//快指针走两步
  26.            if (fastPtr != NULL && fastPtr->next != NULL) {
  27.                fastPtr = fastPtr->next;//快指针走两步
  28.            }
  29.        }
  31.        //第一步  递归，排序右半
  32.        ListNode * rightList = mergeSort(slowPtr->next);
  33.        slowPtr->next = NULL;//将左右两部分切开
  34.        //第二步 递归，排序左半
  35.        ListNode * leftList = mergeSort(head);
  37.        //第三步 合并
  38.        ListNode *pHead = NULL, *pEnd = NULL;//合并链表的头、尾
  39.        if (rightList == NULL) {
  40.            return leftList;
  41.        }
  42.        //初始化头结点、尾节点
  43.        if (rightList->val > leftList->val) {
  44.            pEnd = pHead = leftList;
  45.            leftList = leftList->next;
  46.        }
  47.        else {
  48.            pEnd = pHead = rightList;
  49.            rightList = rightList->next;
  50.        }
  51.        //合并，每次将较小值放入新链表
  52.        while (rightList && leftList) {
  53.            if (rightList->val > leftList->val) {
  54.                pEnd->next = leftList;
  55.                pEnd = pEnd->next;
  56.                leftList = leftList->next;
  57.            }
  58.            else {
  59.                pEnd->next = rightList;
  60.                pEnd = pEnd->next;
  61.                rightList = rightList->next;
  62.            }
  63.        }
  64.        //可能某个链表有剩余
  65.        if (rightList == NULL) {
  66.            pEnd->next = leftList;
  67.        }
  68.        else {
  69.            pEnd->next = rightList;
  70.        }
  71.        return pHead;
  72.    }
  73. };

环形链表 II

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。
说明：不允许修改给定的链表。
示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：tail connects to node index 1
解释：链表中有一个环，其尾部连接到第二个节点。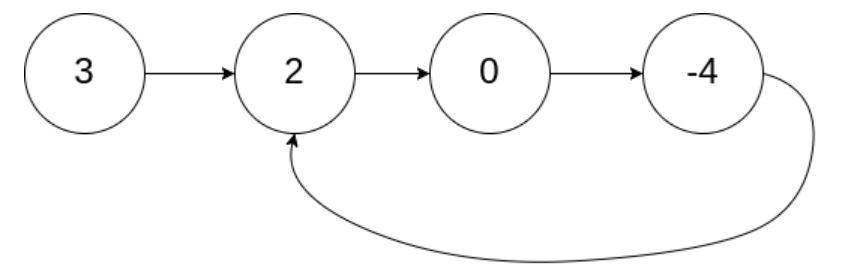
image.png
示例 2：
输入：head = [1,2], pos = 0
输出：tail connects to node index 0
解释：链表中有一个环，其尾部连接到第一个节点。

解法

快慢指针，出现重复之后，慢指针返回到头结点，快指针继续，两者每次都走一步，直到相遇

AC代码

  1. /**
  2. * Definition for singly-linked list.
  3. * struct ListNode {
  4. *     int val;
  5. *     ListNode *next;
  6. *     ListNode(int x) : val(x), next(NULL) {}
  7. * };
  8. */
  9. class Solution {
  10. public:
  11.    ListNode *detectCycle(ListNode *head) {
  12.        if(head == nullptr)
  13.            return nullptr;
  14.        ListNode * slow = head;
  15.        ListNode * fast = head;
  16.        ListNode * temp = nullptr;
  17.        int node = 1;
  18.        while(fast -> next != nullptr){
  19.            slow = slow -> next;
  20.            fast = fast -> next;
  21.            if(fast -> next != nullptr)
  22.                fast = fast -> next;
  23.            else return nullptr;
  24.            if(slow == fast){
  25.                temp = slow;
  26.                break;
  27.            }
  28.        }
  29.        if(temp != nullptr){
  30.            slow = head;
  31.            while(slow != fast){
  32.                slow = slow -> next;
  33.                fast = fast -> next;
  34.            }
  35.            return slow;
  36.        }
  37.        else return nullptr;
  38.    }
  39. };

相交链表

编写一个程序，找到两个单链表相交的起始节点。
如下面的两个链表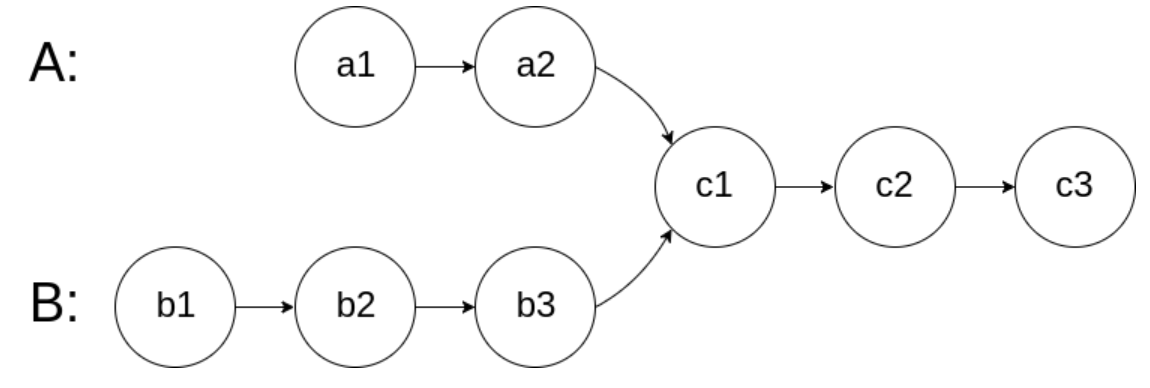
image.png
在节点 c1 开始相交。
示例 1：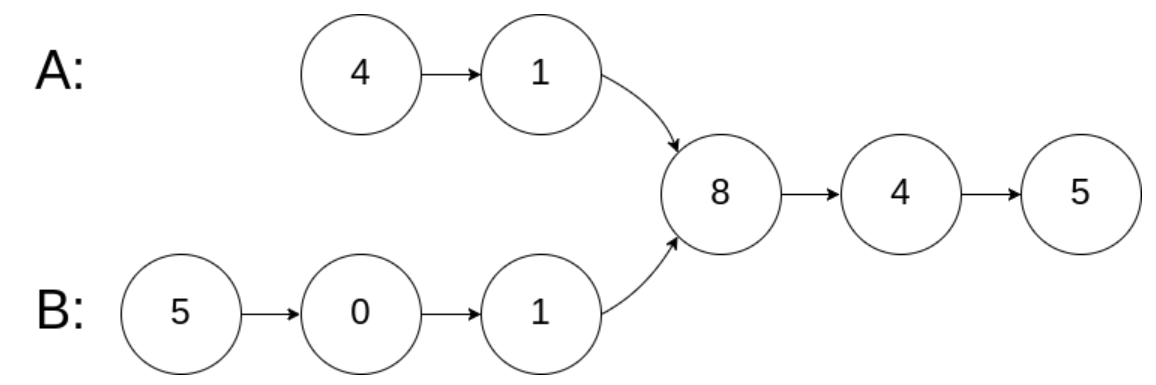
image.png
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Reference of the node with value = 8
输入解释：相交节点的值为 8 （注意，如果两个列表相交则不能为 0）。从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

解法

同时遍历两个链表到尾部，同时记录两个链表的长度。若两个链表最后的一个节点相同，则两个链表相交。 有两个链表的长度后，我们就可以知道哪个链表长，设较长的链表长度为 len1，短的链表长度为len2。 则先让较长的链表向后移动 (len1-len2) 个长度。然后开始从当前位置同时遍历两个链表，当遍历到的链表的节点相同时，则这个节点就是第一个相交的节点。

AC代码

/**
* Definition for singly-linked list.
* struct ListNode {
*     int val;
*     ListNode *next;
*     ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
   ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
       if(headA==NULL || headB==NULL)
           return NULL;
       ListNode *ans1=headA,*ans2=headB;
       while(ans1!=ans2)
       {
           if(ans1==NULL)
               ans1=headB;
           else
               ans1=ans1->next;
           if(ans2==NULL)
               ans2=headA;
           else
               ans2=ans2->next;
       }
       return ans1;
   }
};

合并K个排序链表

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。
示例:
输入:
[
1->4->5,
1->3->4,
2->6
]
输出: 1->1->2->3->4->4->5->6

解法

因为已经做过合并两个有序链表的，所以我们就需要两个两个的合并，直到合并到一个链表中去。

AC代码

class Solution {
public:
   ListNode* mergeKLists(vector<ListNode*>& lists) {
       if (lists.empty()) return NULL;
       int n = lists.size();
       while (n > 1) {
           int k = (n + 1) / 2;
           for (int i = 0; i < n / 2; ++i) {
               lists[i] = mergeTwoLists(lists[i], lists[i + k]);
           }
           n = k;
       }
       return lists[0];
   }
   ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
       ListNode *dummy = new ListNode(-1), *cur = dummy;
       while (l1 && l2) {
           if (l1->val < l2->val) {
               cur->next = l1;
               l1 = l1->next;
           } else {
               cur->next = l2;
               l2 = l2->next;
           }
           cur = cur->next;
       }
       if (l1) cur->next = l1;
       if (l2) cur->next = l2;
       return dummy->next;
   }
};

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。

解法

第一种情况：左子树和右子树均找没有 p 结点或者 q 结点；（这里特别需要注意，虽然题目上说了 p 结点和 q 结点必定都存在，但是递归的时候必须把所有情况都考虑进去， 因为题目给的条件是针对于整棵树，而递归会到局部，不一定都满足整体条件）
第二种情况：左子树上能找到，但是右子树上找不到，此时就应当直接返回左子树的查找结果；
第三种情况：右子树上能找到，但是左子树上找不到，此时就应当直接返回右子树的查找结果；
第四种情况：左右子树上均能找到，说明此时的 p 结点和 q 结点分居 root 结点两侧，此时就应当直接返回 root 结点。

AC代码

* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     TreeNode *left;
*     TreeNode *right;
*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
   TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
       if(root==NULL) return root;
       if(root==p||root==q) return root;
       TreeNode *left=lowestCommonAncestor(root->left,p,q);
       TreeNode *right=lowestCommonAncestor(root->right,p,q);

       if(left!=NULL&&right!=NULL) return root;//如果p,q刚好在左右两个子树上
       if(left==NULL) return right;//仅在右子树
       if(right==NULL) return left;//仅在左子树
   }
};

二叉树的锯齿形层次遍历

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

例如： 给定二叉树 [3,9,20,null,null,15,7],
   3
  / \
 9  20
   /  \
  15   7
返回锯齿形层次遍历如下：
[
 [3],
 [20,9],
 [15,7]
]

解法

其实就是层次遍历，只不过相邻每两层之间输出的顺序相反，所以就设置一个bool型的变量，每次判断是该从左往右，还是从右往在即可。然后每遍历一层，对这个bool型变量取反。

AC代码

public class Solution {
   public List<List<Integer>> data = new ArrayList<List<Integer>>();
   public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
       if(root == null){
           return data;
       }
       Queue<TreeNode> queue = new LinkedList<TreeNode>();
       queue.offer(root);
       int level = 1;
       while(!queue.isEmpty()){
           int size = queue.size();
           List<Integer> list = new ArrayList<Integer>();
           for(int  i = 0; i < size; i++){
               TreeNode node = queue.poll();
               list.add(node.val);
               if(node.left != null){
                   queue.offer(node.left);
               }
               if(node.right != null){
                   queue.offer(node.right);
               }
           }
           if(level % 2 != 0){
               data.add(list);
           }else{
               Collections.reverse(list);
               data.add(list);
           }
           level++;
       }
       return data;
   }
}

判断一颗二叉树是不是一颗二叉搜索树

解法

什么是二叉搜索树？任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值;
根据性质怎么判断一颗二叉树是不是搜索二叉树呢? 其实很简单，只要这颗二叉树的中序遍历的顺序是升序的，那么就是一颗二叉搜索树，因为中序遍历的顺序是左->中->右，所以当中序遍历升序的时候，就有左<中<右，所以就可以判断。

AC代码

class Solution {
   public boolean isValidBST(TreeNode root) {
       if(root == null)
           return true;
       Stack<TreeNode>stack = new Stack<>();
       TreeNode cur = root;
       TreeNode pre = null;
       while(!stack.isEmpty() || cur != null){
           if(cur != null){
               stack.push(cur);
               cur = cur.left;
           }else {
               cur = stack.pop();
               if(pre != null && cur.val <= pre.val)
                   return false;
               pre = cur;
               cur = cur.right;
           }
       }
       return true;
   }
}

判断一个二叉树为完全二叉树

解法

判断过程：
按照层次遍历的顺序遍历二叉树，每一层从左到右；
如果当前结点有右孩子但没有左孩子，直接返回 false；
如果当前结点不是左右孩子都全(包括两种情况)，那之后的结点必须都为叶节点，否则返回 false；
遍历过程中如果没有返回 false，就返回 true；

AC代码

//判断一棵二叉树是不是完全二叉树
   static boolean isCBT(TreeNode root){
       if(root == null)
           return true;
       Queue<TreeNode>queue = new LinkedList<>();
       boolean leaf = false; //如果碰到了 某个结点孩子不全就开始　判断是不是叶子这个过程
       queue.add(root);
       TreeNode top = null,L = null,R = null;
       while(!queue.isEmpty()){
           top = queue.poll();
           L = top.left;  R = top.right;
           //第一种情况
           if((R != null && L == null))
               return false;
           //第二种情况  开启了判断叶子的过程 而且又不是叶子 就返回false
           if(leaf && (L != null || R != null)) //以后的结点必须是 左右孩子都是null
               return false;
           if(L != null)
               queue.add(L);
           //准确的说是　只要孩子不全就开启leaf，
           //但是前面已经否定了有右无左的情况，这里只要判断一下右孩子是不是为空就可以了(如果为空就开启leaf)
           if(R != null)
               queue.add(R);
           else
               leaf = true;
       }
       return true;
   }