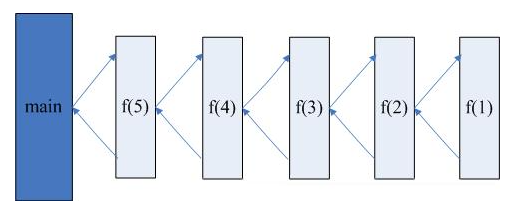
什么是递归

在数学与计算机科学中，递归(Recursion)是指在函数的定义中使用函数自身的方法（自己调用自己）。实际上，递归，顾名思义，其包含了两个意思：递 和 归，这正是递归思想的精华所在

递归的核心思想

递归就是有去（递去）有回（归来），如下图所示。“有去”是指：递归问题必须可以分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决。“有回”是指 : 这些问题的演化过程是一个从大到小，由近及远的过程，并且会有一个明确的终点(临界点)，一旦到达了这个临界点，就不用再往更小、更远的地方走下去。最后，从这个临界点开始，原路返回到原点，原问题解决。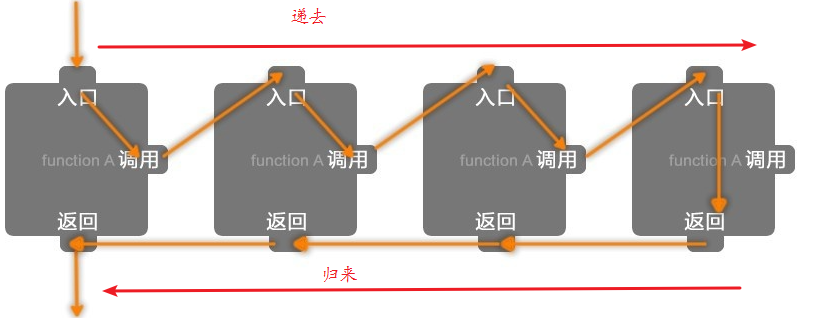递归算法 - 图1

案例

求 5 的阶乘
递归算法 - 图2

关键点

直接地说，递归的基本思想就是把规模大的问题转化为规模小的相似的子问题来解决。特别地，在函数实现时，因为解决大问题的方法和解决小问题的方法往往是同一个方法，所以就产生了函数调用它自身的情况，这也正是递归的定义所在。格外重要的是，这个解决问题的函数必须有明确的结束条件，否则就会导致无限递归的情况（死循环）

递归必须满足以下的条件

  • 明确递归终止条件；
  • 给出递归终止时的处理办法；
  • 提取重复的逻辑，缩小问题规模

    案例

    求 5 的阶乘 ：

    /*
     计算 参数 i 的阶乘
    @param i
     @return
    /
    static long jc(int i){
    if(i==1) {
    return 1;
    }else {
    return i     jc(i-1);
    }
    }

    斐波纳契数列

    1 1 2 3 5 8 13 21 34 55 …….n前两个数的和等于第三个数 /*
    @param n 第几个数
    fun(n) = fun(n-2) + fun(n-1) // n=1 或者 你=2 的时候 结构 都是 1
    @return
    /
    //1 1 2 3 5 8 13 21 34 55 …….n
    static int fun(int n){
    if(n == 1 || n == 2){
    return 1 ;
    }else {
    return fun(n-1) +fun(n-2);
    }
    }

    二分查找

    有一个已经排序过的 数组或者集合 ，首先我们找到一个中间值 和 目的数据进行比较int binarySearch(int left ,int right,int key){

    }
    面试题 : 递归和循环 哪一个效率较高
    循环的效率比递归的效率要高 ，在递归的过程中 ，方法需要时刻的入栈，方法一旦入栈，内存就要给方法的参数分配空间 ，空间只有到递归结束的时候才会释放， 所以递归很耗内存，循环没有方法入栈 ，不需要时刻的分配内存，