二叉树

二叉树的定义

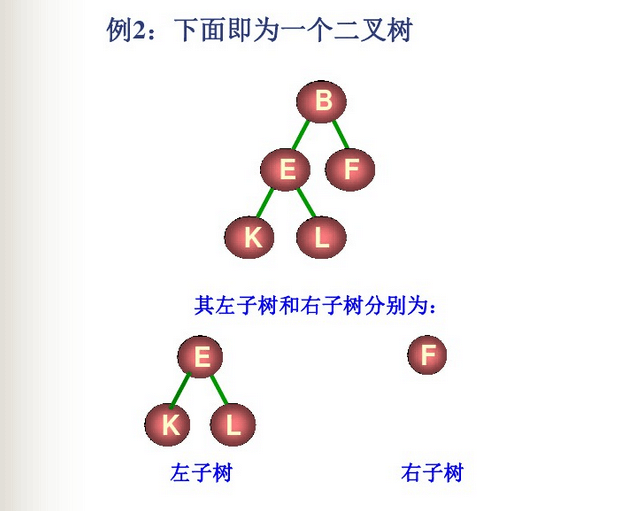
是n（n >= 0）个结点的有限集合，它或为空树（n = 0），或是由一个根结点加上两颗称为左子树和右子树的、互不相交的二叉树组成。

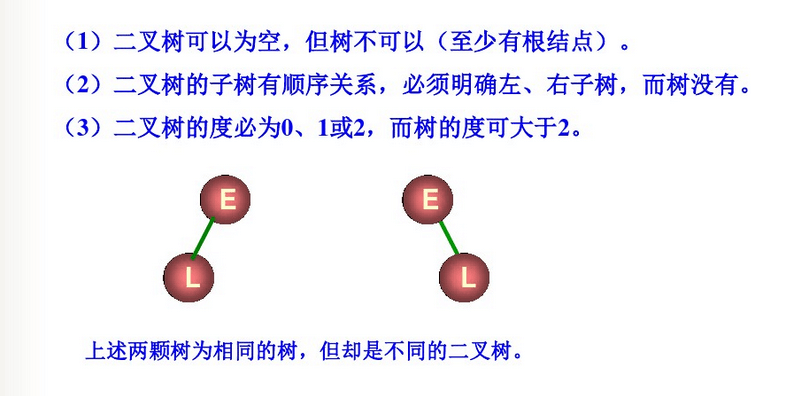
二叉树中部存在度大于2的结点，并且二叉树的子树有左子树和右子树之分，也即二叉树的子树有顺序关系。

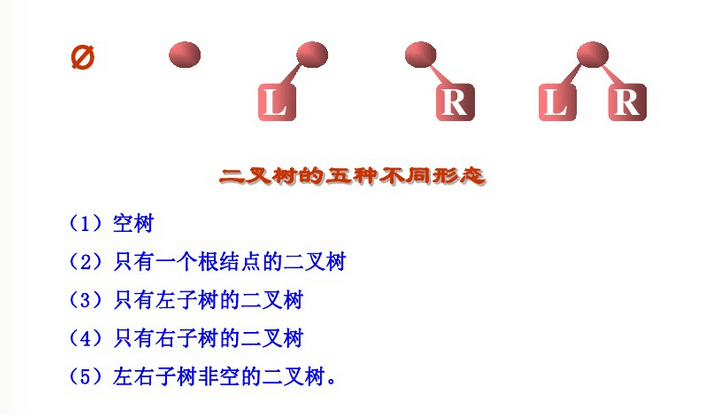
二叉树的五种形态

二叉树和树的比较

二叉树的相关特点

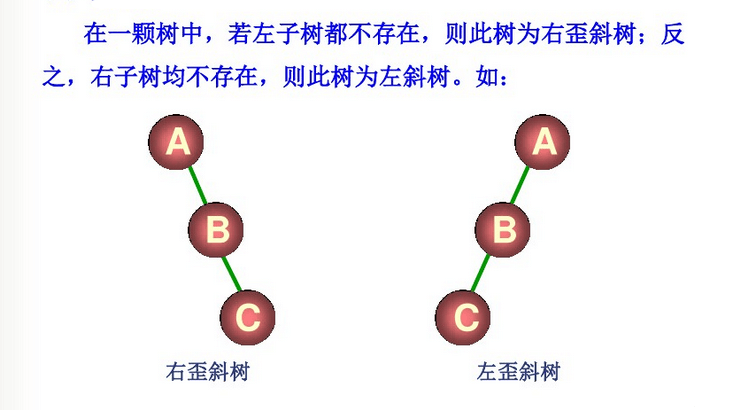
1. 歪斜树

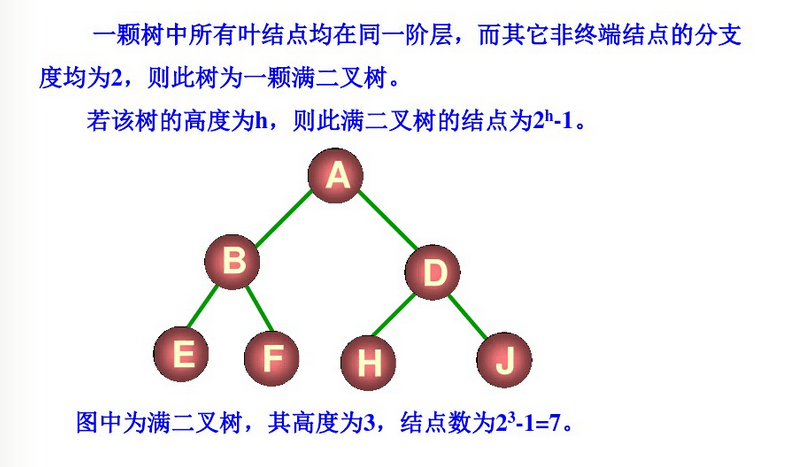
2. 满二叉树

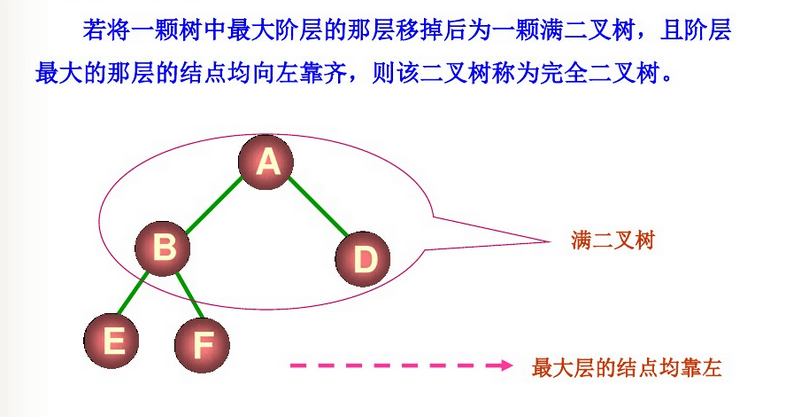
3. 完全二叉树

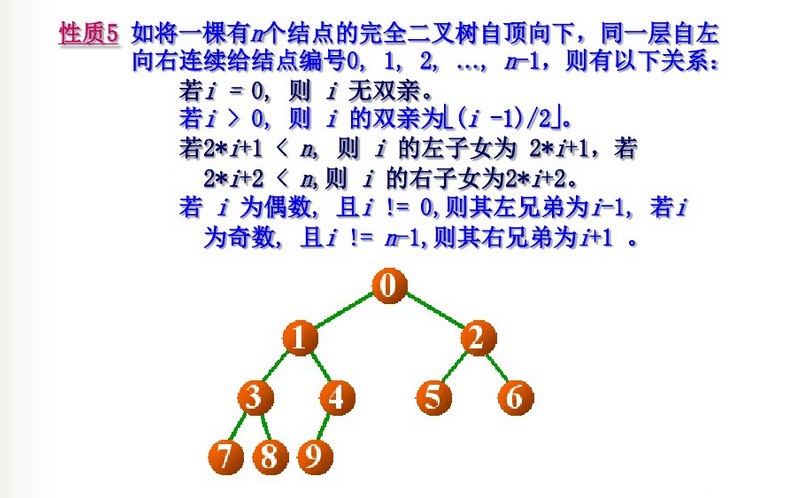
二叉树的特性

二叉树的表示法（存储）

其中前两种方法属于静态内存空间配置，后一种方法属于动态内存空间配置。

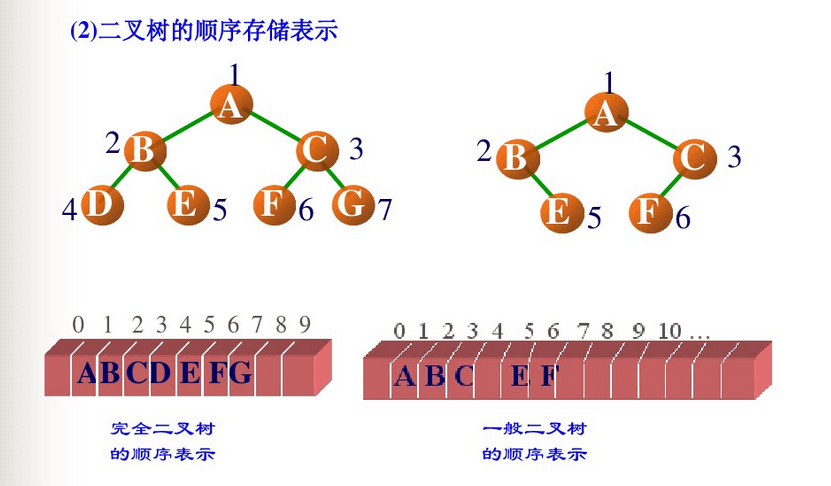
1. 二叉树顺序（数组）表示

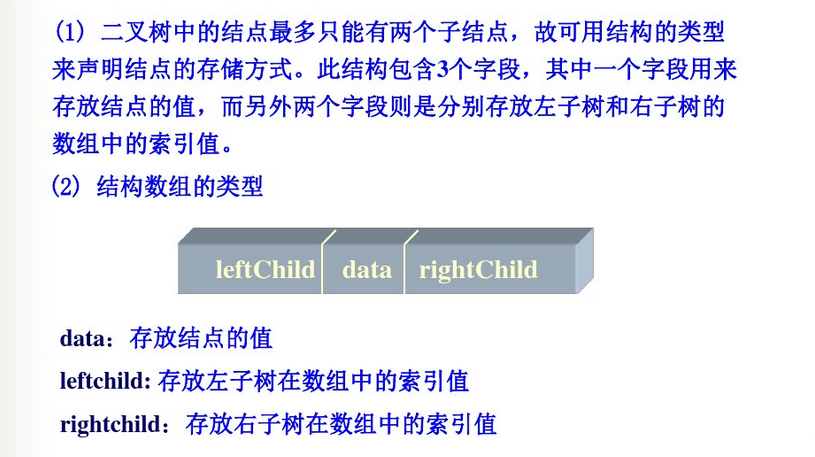
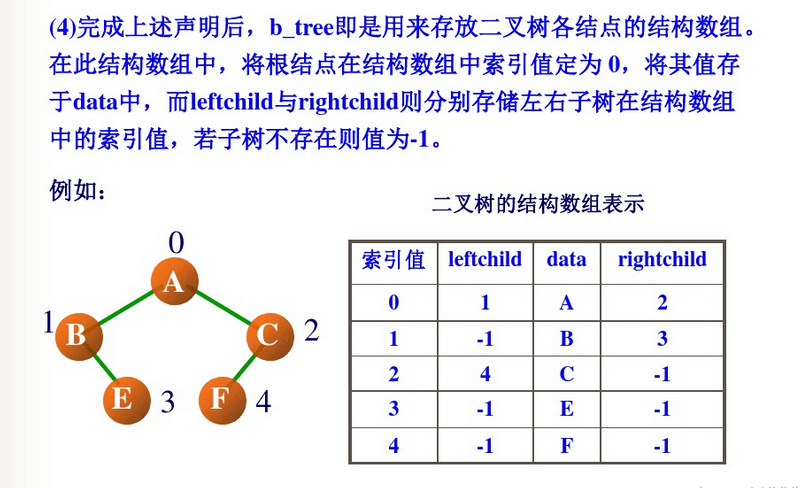
2. 二叉树结构数组表示

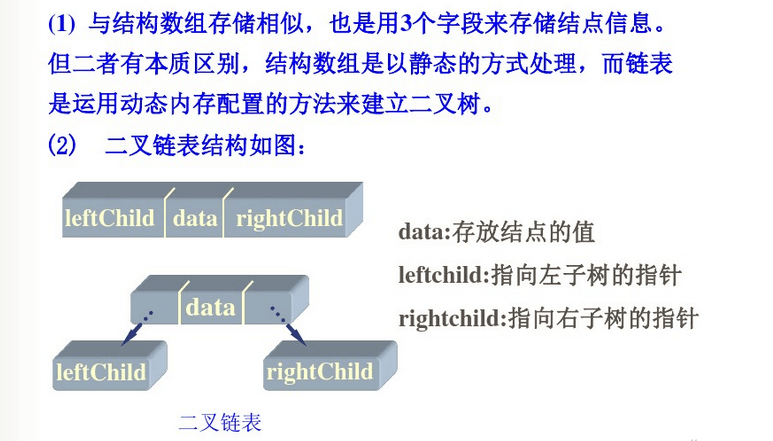
3. 二叉树链表表示

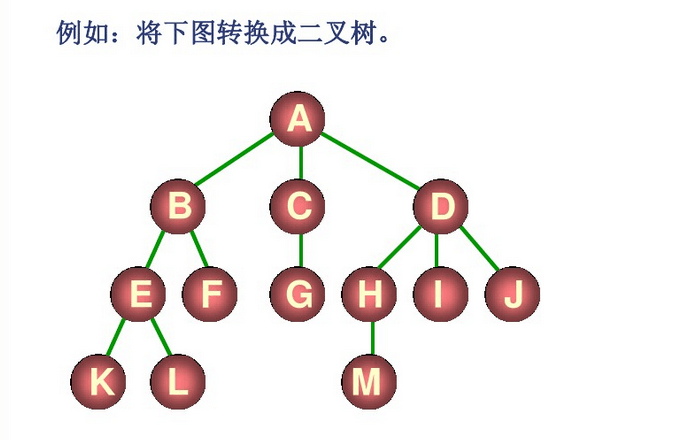
一般树转换成二叉树

即将度为 n 的树，变成不超过2个分支的树，其步骤为：

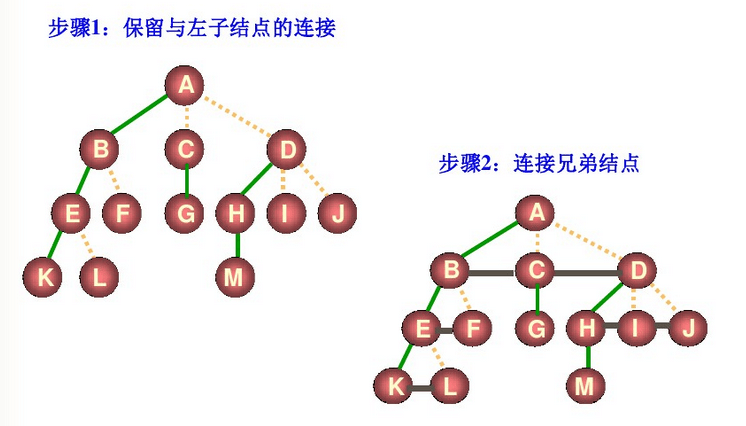
1. 保留所有结点与其左子结点的链接
2. 连结所有同一父结点的子结点
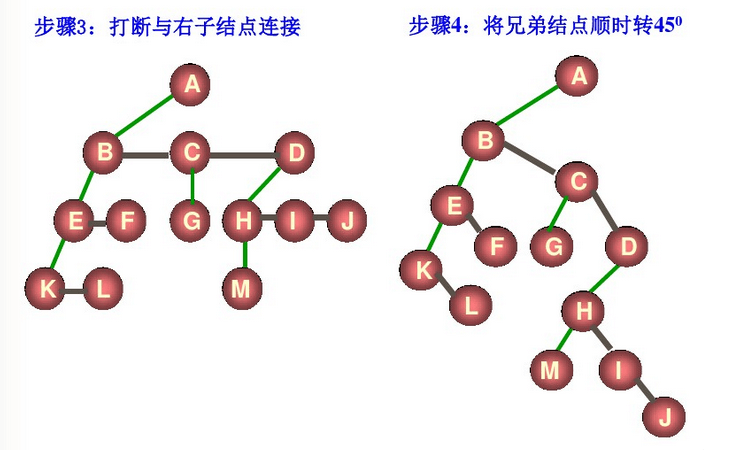
3. 打断所有结点原本与右子结点的链接
4. 将兄弟结点顺时转45度

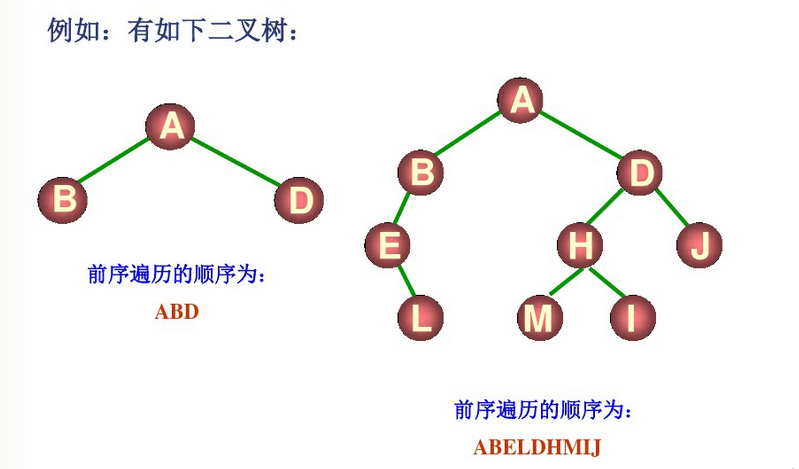
二叉树的遍历

“二叉树的遍历”就是按某种次序访问树中的结点，要求每个结点访问一次且仅访问一次。
每个结点均有左右两个分支，在遍历的过程中选择往左或往右走，遍历结束，每个结点恰好被访问一次。
事实上，二叉树的遍历是以递归的方式进行，依递归的调用顺序不同，可分为下列三种不同的遍历方式。

• 前序遍历方式
• 中序遍历方式

• 后序遍历方式

  1. 二叉树的前序遍历

  若二叉树为空，则空操作，否则：

• 访问目前结点

• 前序遍历左子树
• 前序遍历右子树

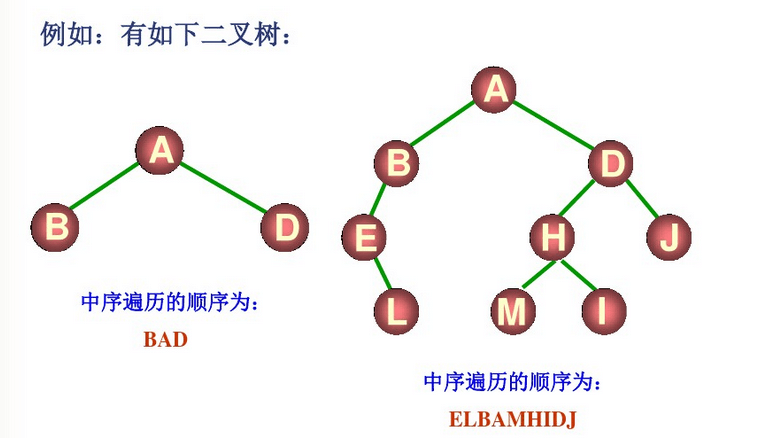
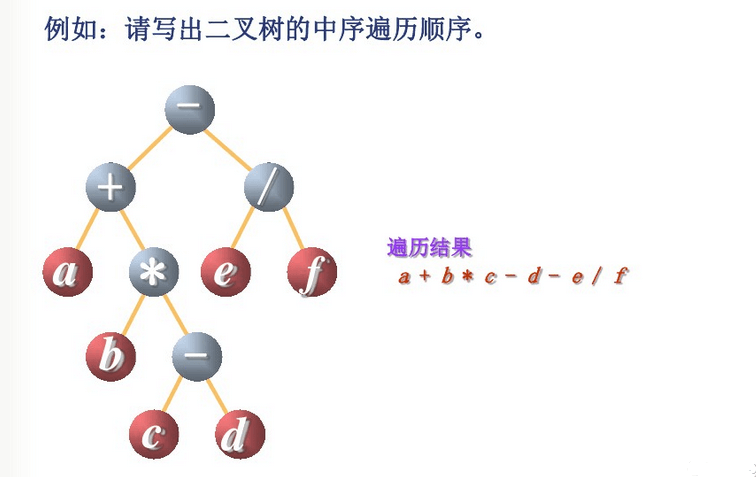
2. 二叉树的中序遍历

若二叉树为空，则空操作，否则：

• 中序遍历左子树
• 访问根结点
• 中序遍历右子树

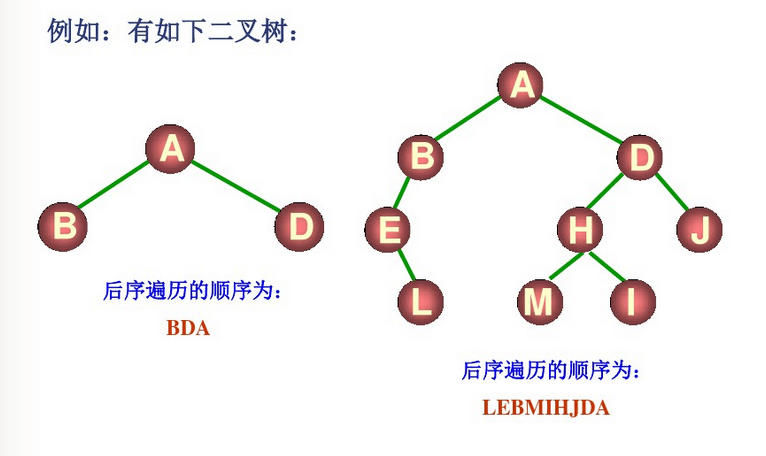
3. 二叉树的后序遍历

若二叉树为空，则空操作，否则：

• 后序遍历左子树
• 后序遍历右子树
• 访问根结点