参考博客:http://www.cnblogs.com/wuliytTaotao/archive/2018/09/15/9560205.html
https://blog.csdn.net/wux_j/article/details/84823002
https://blog.csdn.net/wsp_1138886114/article/details/82080881
残差网络 (residual network):
DNN 为什么不是越深越好:
论文认为,可以训练一个 shallower 网络,然后在这个训练好的 shallower 网络上堆几层 identity mapping(恒等映射) 的层,即输出等于输入的层,构建出一个 deeper 网络。这两个网络(shallower 和 deeper)得到的结果应该是一模一样的,因为堆上去的层都是 identity mapping。这样可以得出一个结论:理论上,在训练集上,Deeper 不应该比 shallower 差,即越深的网络不会比浅层的网络效果差。
在不断加深神经网络的深度时,会出现退化 (Degradation) 问题,即准确率会先上升然后达到饱和,再持续增加深度会导致准确率下降。这并不是过拟合问题,因为不光在测试集上误差增大,训练集本身误差也会增大。原因是随着网络越来越深,训练变得原来越难,网络的优化变得越来越难。理论上,越深的网络,效果应该更好;但实际上,由于训练难度,过深的网络会产生退化问题,效果反而不如相对较浅的网络。而残差网络就可以解决这个问题的,残差网络越深,训练集上的效果会越好。(测试集上的效果可能涉及过拟合问题)
假设有比较浅的网络达到了饱和的准确率,那么后面再加上集几个 y = x y=x y\=x 的恒等映射层 (identity mapping),起码误差不会增加,即更深的网络不应该带来训练集上误差的上升。恒等映射层 y = x y=x y\=x 直接将前一层输出传到后面的思想,是 ResNet 的主要创新点。
残差模块 (Residual Block)
残差是指实际观察值与估计值(拟合值)之间的差,某个残差块的输入为 x x x,拟合的输出为 H (x) H(x) H(x), 如果我们直接把输入 x x x 直接传到输出作为观测结果,那么我们需要学习的残差就是 F ( x ) = H ( x ) − x F(x)=H(x)-x F(x)\=H(x)−x。下图是一个残差学习单元。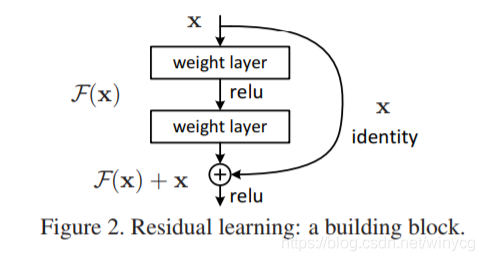
残差块的计算方式为: F (x) = W 2 ⋅ r e l u ( W 1 x ) F(x)=W{2}\cdot relu(W{1}x) F(x)\=W2⋅relu(W1x),
残差块的输出为 r e l u (H ( x) ) = r e l u ( F ( x ) + x ) relu(H(x))=relu(F(x)+x) relu(H(x))\=relu(F(x)+x).
残差块误差优化: 残差网络通过加入 shortcut connections(或称为 skip connections),变得更加容易被优化。在不用 skip 连接之前,假设输入是 x x x,最优输出是 x x x,此时的优化目标是预测输出 H (x) = x H(x)=x H(x)\=x,加入 skip 连接后,优化输出 H ( x ) H(x) H(x) 与输入 x x x 的差别,即为残差 F ( x ) = H ( x ) − x F(x)=H(x)-x F(x)\=H(x)−x,此时的优化目标是 F ( x ) F(x) F(x) 的输出值为 0。后者会比前者更容易优化。
用残差更容易优化:引入残差后的映射对输出的变化更敏感。设 H 1 (x) H{1}(x) H1(x) 是加入 skip 连接前的网络映射, H 2 ( x ) H{2}(x) H2(x) 是加入 skip 连接的网络映射。对于输入 x = 5 x=5 x\=5,设此时 H 1 ( 5 ) = 5.1 H{1}(5)=5.1 H1(5)\=5.1, H 2 ( x ) = 5.1 , H 2 ( 5 ) = F ( 5 ) + 5 , F ( 5 ) = 0.1 H{2}(x)=5.1,H{2}(5)=F(5)+5,F(5)=0.1 H2(x)\=5.1,H2(5)\=F(5)+5,F(5)\=0.1。当输出变为 5.2 时, H 1 ( x ) H{1}(x) H1(x) 由 5.1 变为 5.2, F ( x ) F(x) F(x) 由 0.1 变为 0.2,明显后者输出变化对权重的调整作用更大,所以效果更好。残差的思想都是去掉相同的主体部分,从而突出微小的变化。
简单的加法不会给网络增加额外的参数和计算量,同时可以大大增加模型的训练速度,提高训练效果。并且当模型的层数加深时,能够有效地解决退化问题。
残差网络为什么是有效的:对于大型的网络,无论把残差块添加到神经网络的中间还是末端,都不会影响网络的表现。因为可以给残差快中的 weight 设置很大的 L2 正则化水平,使得 F (x) = 0 F(x)=0 F(x)\=0,这样使得加入残差块至少不会使得网络变差,此时的残块等价于恒等映射。若此时残差块中的 weight 学到了有用的信息,那就会比恒等映射更好,对网络的性能有帮助。
总结: ResNet 有很多旁路支线可以将输入直接连到后面的层,使得后面的层可以直接学习残差,简化了学习难度。传统的卷积层和全连接层在信息传递时,或多或少会存在信息丢失,损耗等问题。ResNet 将输入信息绕道传到输出,保护了信息的完整性。
ResNet 网络结构
在 ResNet 中,使用两个 3x3 的卷积层替换为 1x1 + 3x3 + 1x1 的卷积进行计算优化: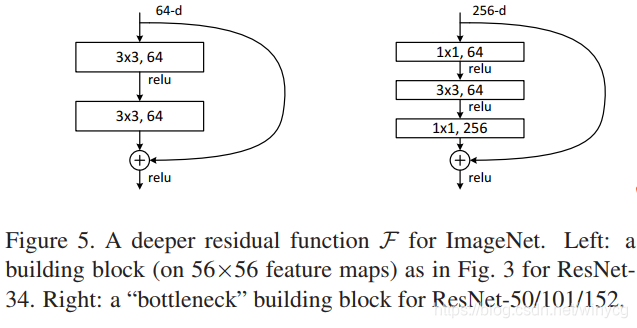
结构中的中间 3x3 的卷积层首先在一个降维 1x1 卷积层下减少了计算,然后在另一个 1x1 的卷积层下做了还原,既保持了精度又减少了计算量,这种结构称为bottleneck 模块。输入和输出要保持相同的维度,若特征图维度不同,对于卷积层的残差块,需要将 x x x 添加卷积核批标准化处理:
若是在全连接层,对 x x x 进行线性映射变换维度,再连接到后面的层。
作者提出的 50、101、152 层的 ResNet 中应用了 bottleneck,而且不仅没有出现退化问题,错误率也大大降低,同时计算复杂度也保持在很低的程度。作者又提出了 1202 层的网络,对于这么深的网络,优化依然并不困难,但是出现了过拟合的问题。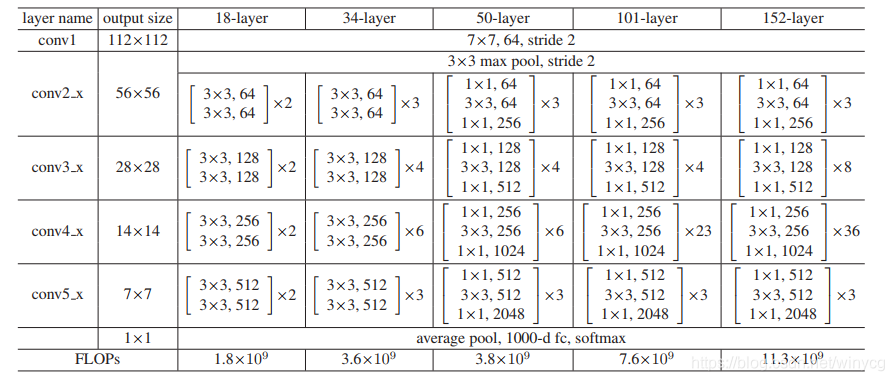
实现上述表格中的 ResNet 结构:
import torchimport torch.nn as nnimport torch.nn.functional as Fclass BasicBlock(nn.Module):expansion = 1def __init__(self, in_planes, planes, stride=1):super(BasicBlock, self).__init__()self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=3,stride=stride, padding=1, bias=False)self.bn1 = nn.BatchNorm2d(planes)self.conv2 = nn.Conv2d(planes, planes, kernel_size=3,stride=1, padding=1, bias=False)self.bn2 = nn.BatchNorm2d(planes)self.shortcut = nn.Sequential()if stride != 1 or in_planes != self.expansion*planes:self.shortcut = nn.Sequential(nn.Conv2d(in_planes, self.expansion*planes,kernel_size=1, stride=stride, bias=False),nn.BatchNorm2d(self.expansion*planes))def forward(self, x):out = F.relu(self.bn1(self.conv1(x)))out = self.bn2(self.conv2(out))out += self.shortcut(x)out = F.relu(out)return outclass Bottleneck(nn.Module):expansion = 4def __init__(self, in_planes, planes, stride=1):super(Bottleneck, self).__init__()self.conv1 = nn.Conv2d(in_planes, planes, kernel_size=1, bias=False)self.bn1 = nn.BatchNorm2d(planes)self.conv2 = nn.Conv2d(planes, planes, kernel_size=3,stride=stride, padding=1, bias=False)self.bn2 = nn.BatchNorm2d(planes)self.conv3 = nn.Conv2d(planes, self.expansion*planes,kernel_size=1, bias=False)self.bn3 = nn.BatchNorm2d(self.expansion*planes)self.shortcut = nn.Sequential()if stride != 1 or in_planes != self.expansion*planes:self.shortcut = nn.Sequential(nn.Conv2d(in_planes, self.expansion*planes,kernel_size=1, stride=stride, bias=False),nn.BatchNorm2d(self.expansion*planes))def forward(self, x):out = F.relu(self.bn1(self.conv1(x)))out = F.relu(self.bn2(self.conv2(out)))out = self.bn3(self.conv3(out))out += self.shortcut(x)out = F.relu(out)return outclass ResNet(nn.Module):def __init__(self, block, num_blocks, num_classes=10):super(ResNet, self).__init__()self.in_planes = 64self.conv1 = nn.Conv2d(3, 64, kernel_size=3,stride=1, padding=1, bias=False)self.bn1 = nn.BatchNorm2d(64)self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)self.linear = nn.Linear(512*block.expansion, num_classes)def _make_layer(self, block, planes, num_blocks, stride):strides = [stride] + [1]*(num_blocks-1)layers = []for stride in strides:layers.append(block(self.in_planes, planes, stride))self.in_planes = planes * block.expansionreturn nn.Sequential(*layers)def forward(self, x):out = F.relu(self.bn1(self.conv1(x)))out = self.layer1(out)out = self.layer2(out)out = self.layer3(out)out = self.layer4(out)out = F.avg_pool2d(out, 4)out = out.view(out.size(0), -1)out = self.linear(out)return outdef ResNet18():return ResNet(BasicBlock, [2,2,2,2])def ResNet34():return ResNet(BasicBlock, [3,4,6,3])def ResNet50():return ResNet(Bottleneck, [3,4,6,3])def ResNet101():return ResNet(Bottleneck, [3,4,23,3])def ResNet152():return ResNet(Bottleneck, [3,8,36,3])def test():net = ResNet18()y = net(torch.randn(1,3,32,32))print(y.size())

